吉林大学学报(工学版) ›› 2024, Vol. 54 ›› Issue (4): 902-916.doi: 10.13229/j.cnki.jdxbgxb.20221637
含多种碰撞约束振动系统的周期运动转迁特性
- 1.兰州交通大学 机电工程学院,兰州 730070
2.兰州交通大学 甘肃省轨道交通装备系统动力学与可靠性重点实验室,兰州 730070
Periodic motion transition characteristics of a vibro-impact system with multiple impact constraints
Shi-jun WANG1,2( ),Guan-wei LUO2
),Guan-wei LUO2
- 1.School of Mechatronic Engineering,Lanzhou Jiaotong University,Lanzhou 730070,China
2.Key Laboratory of System Dynamics and Reliability of Rail Transport Equipment of Gansu Province,Lanzhou 730070,China
摘要:
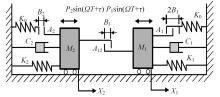
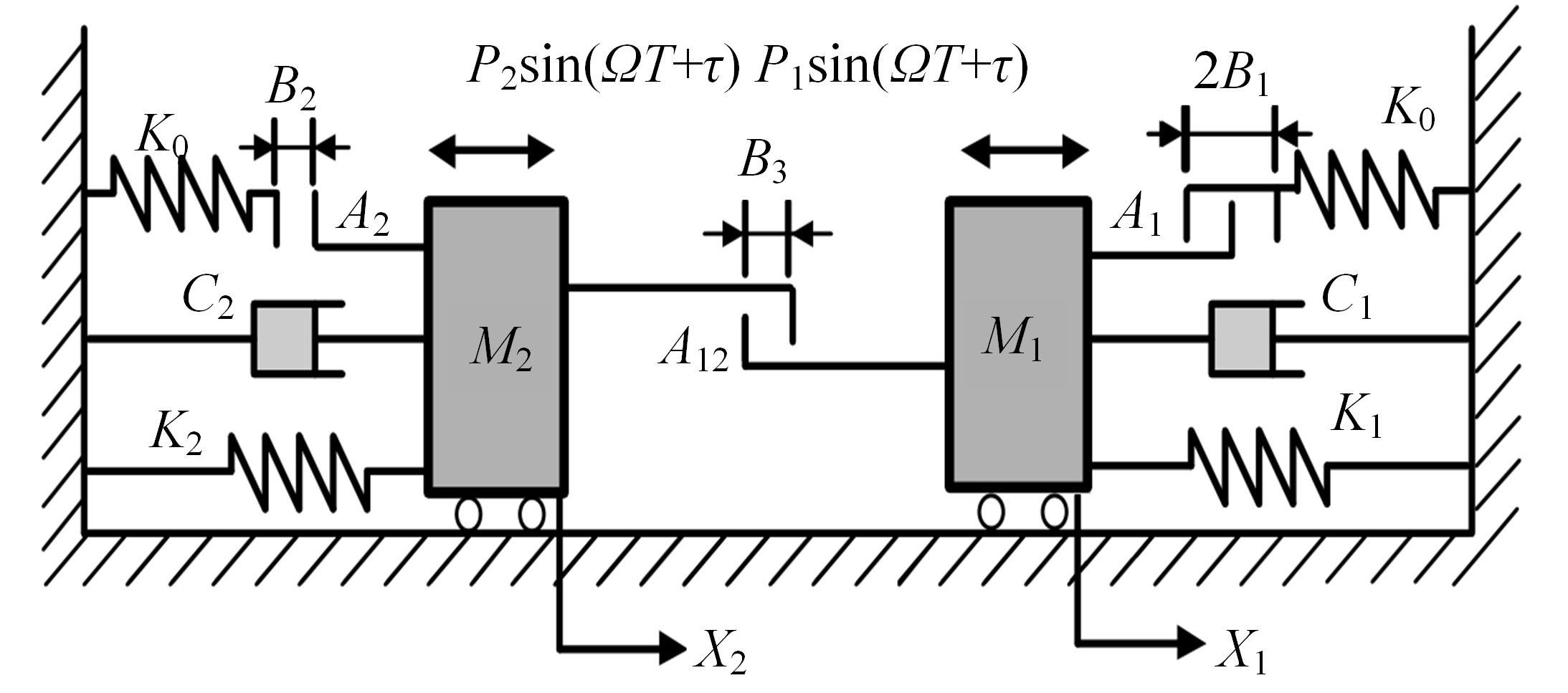
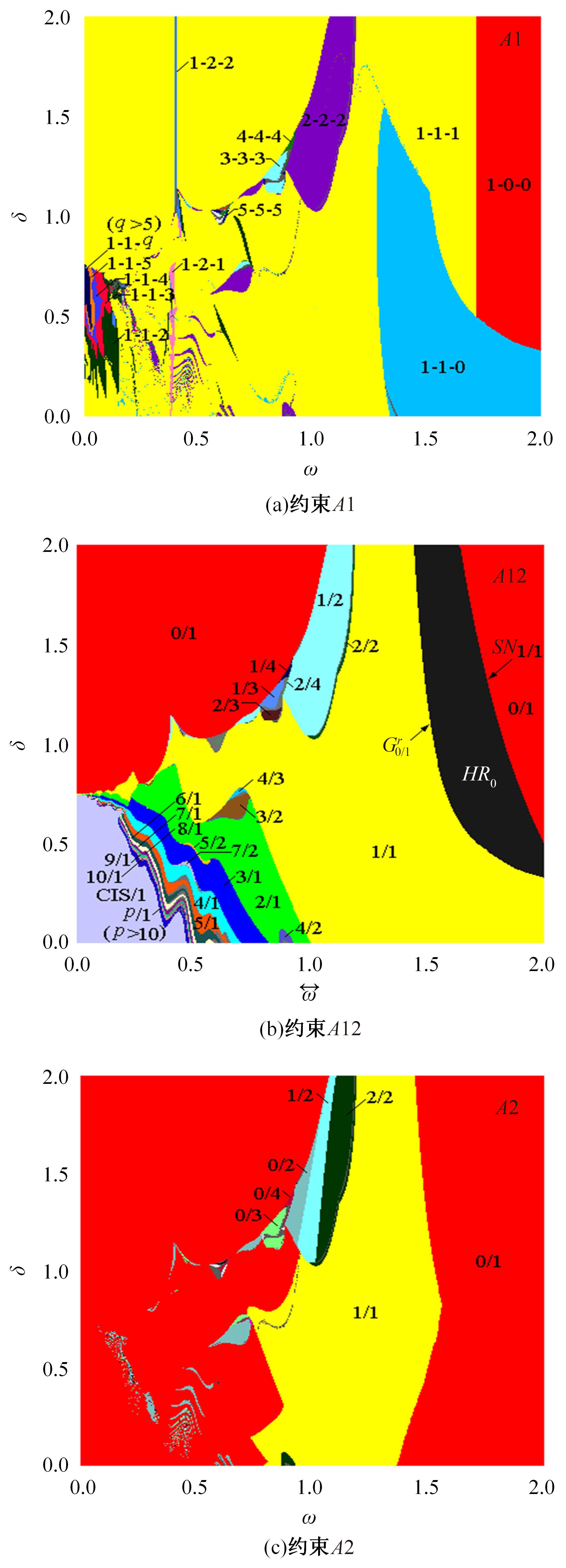
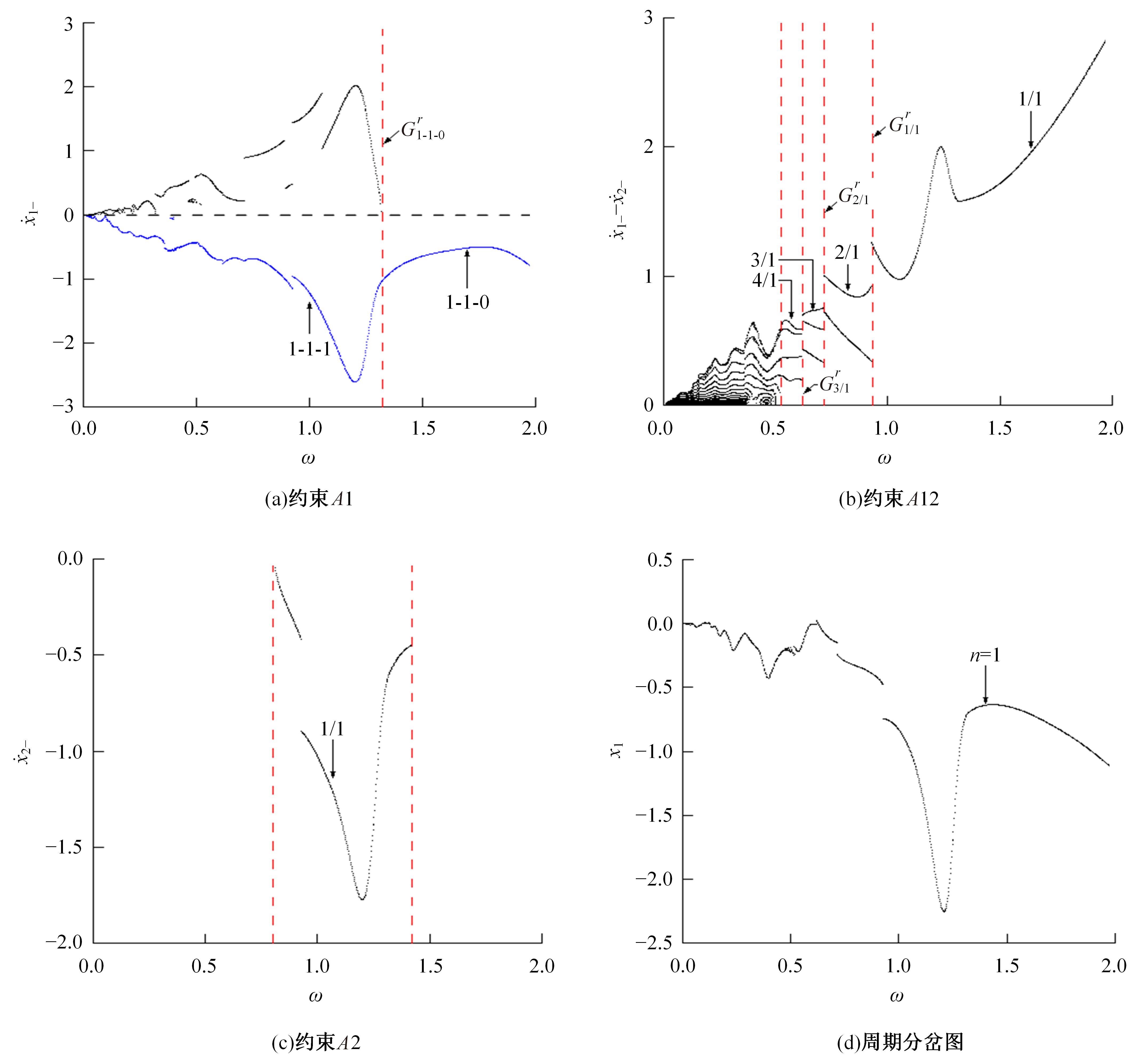
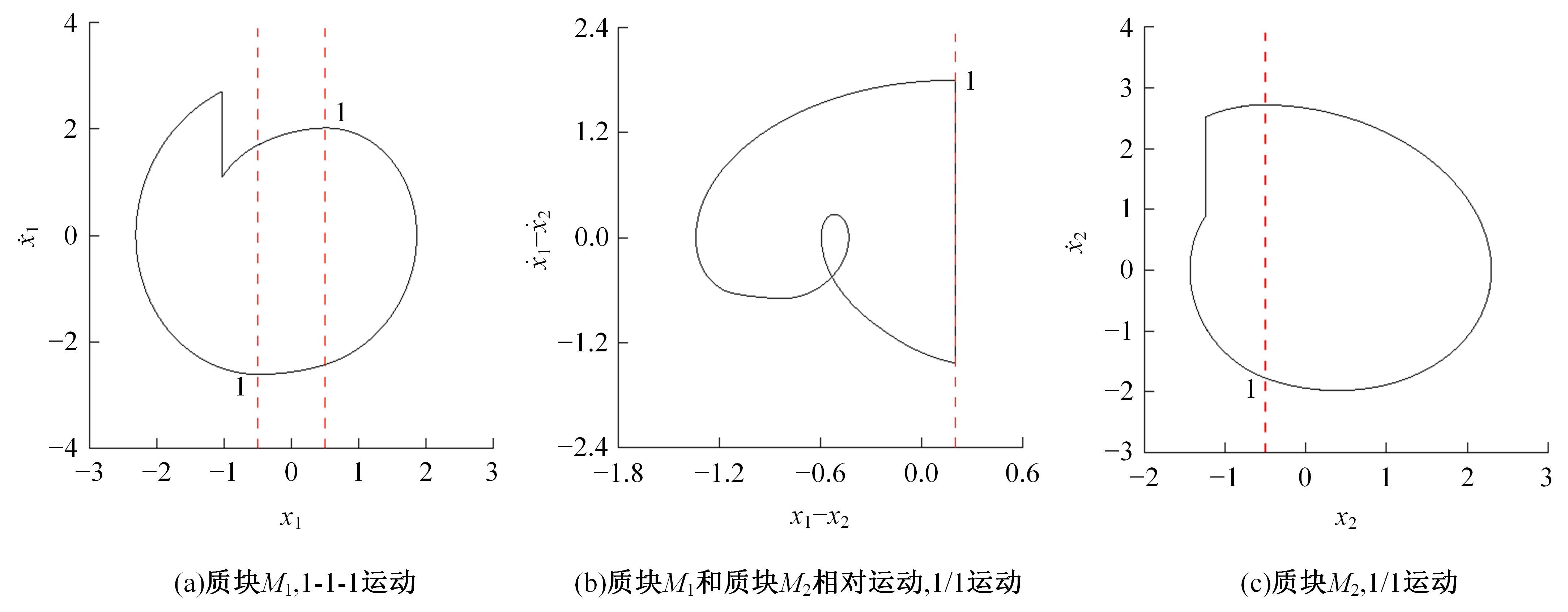
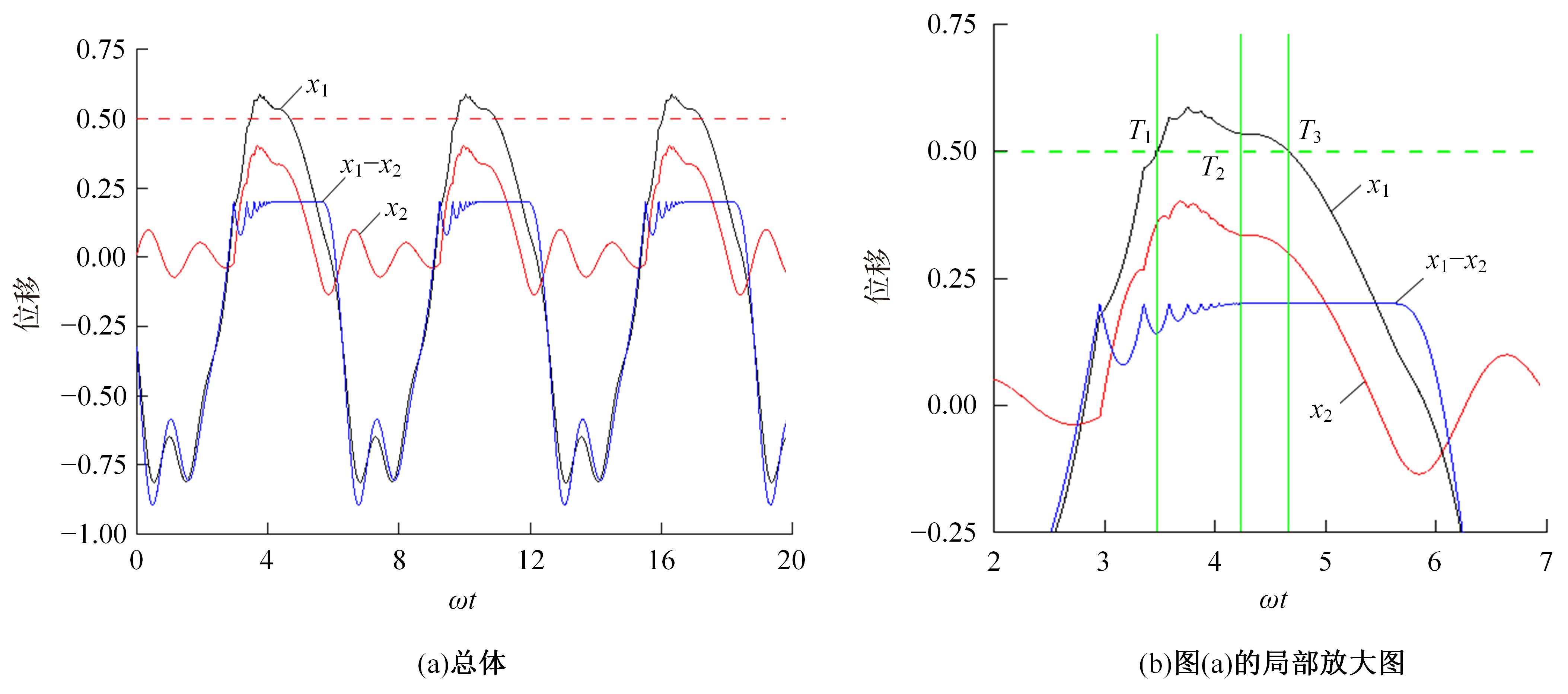
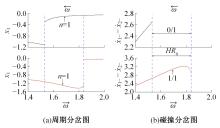
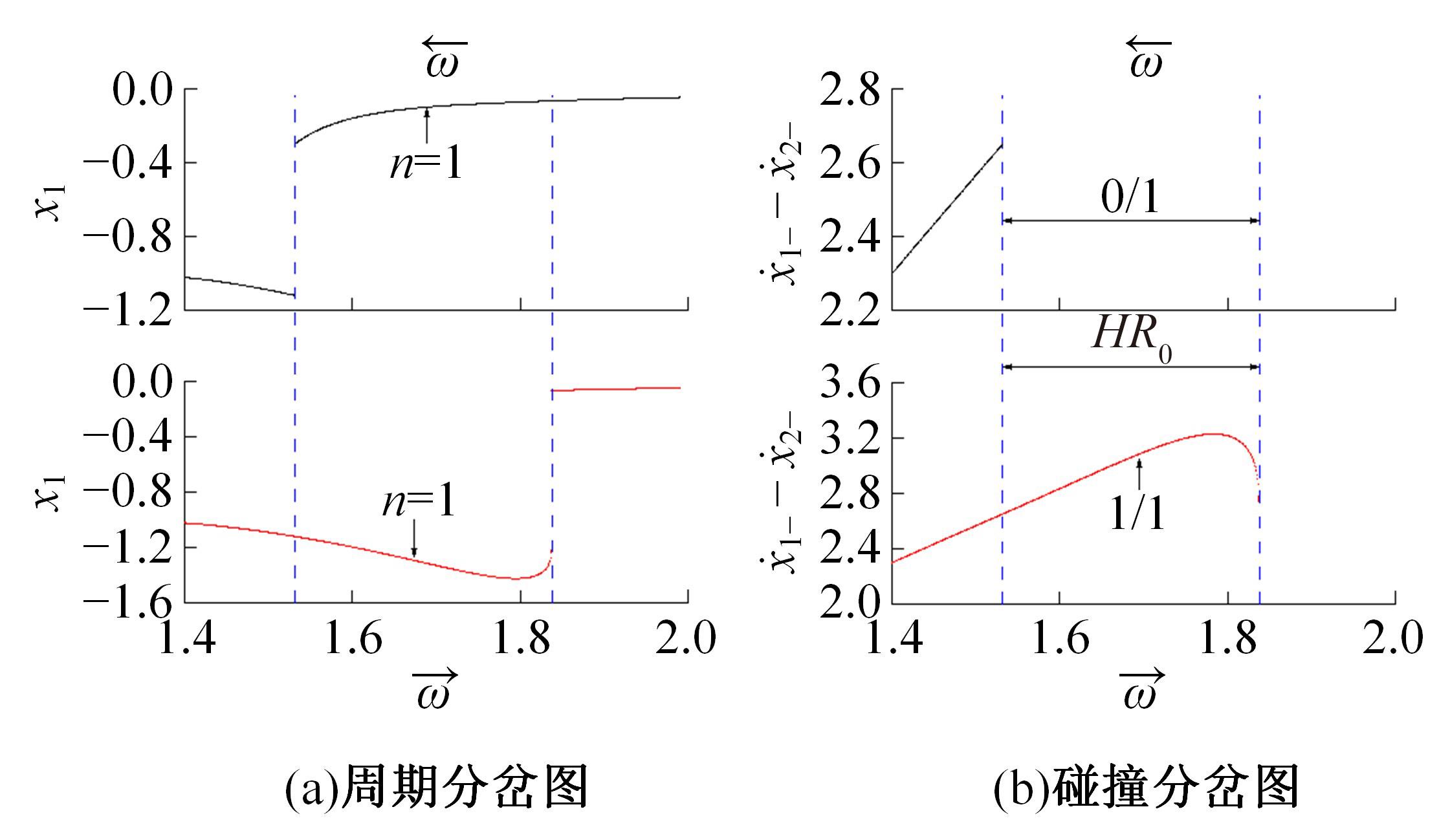
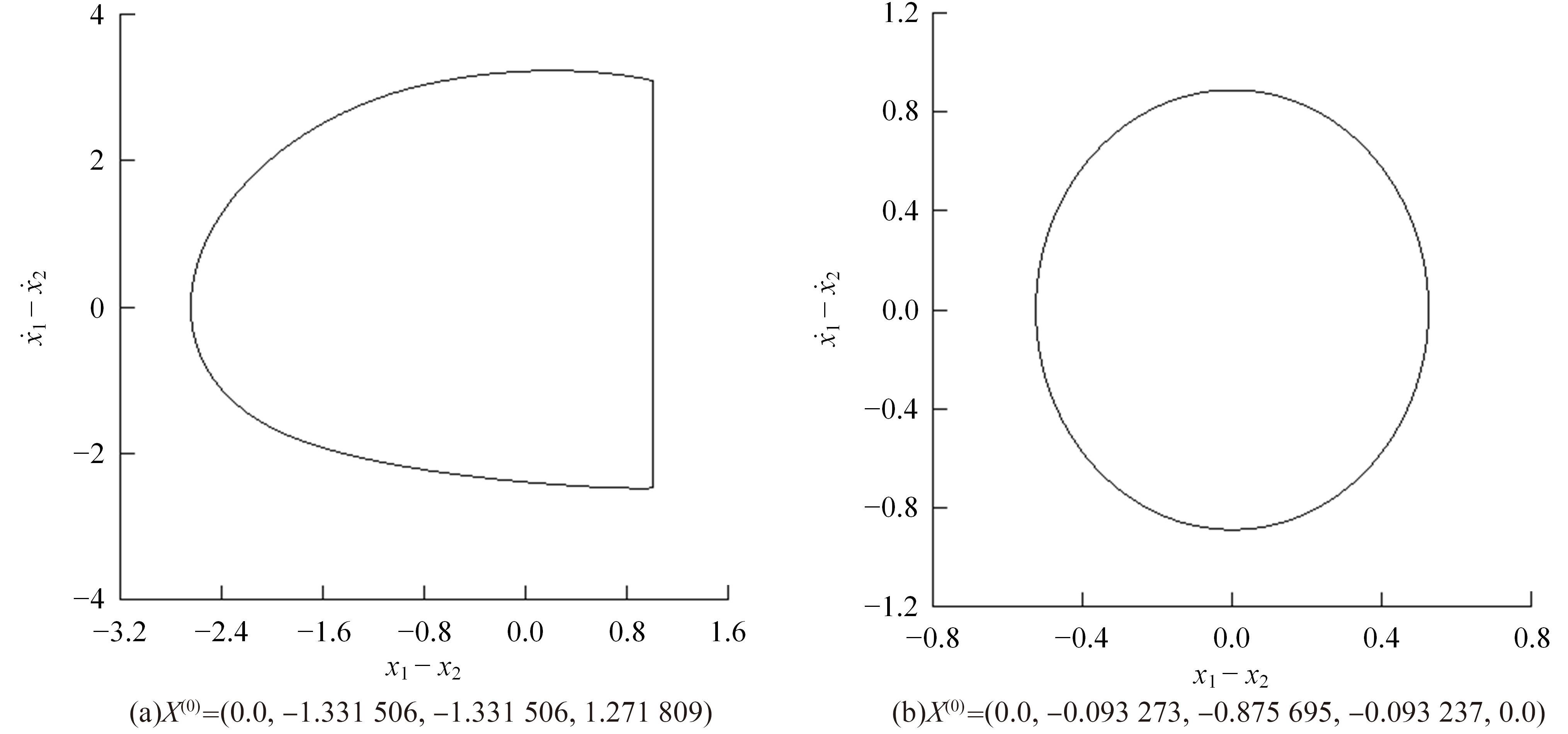
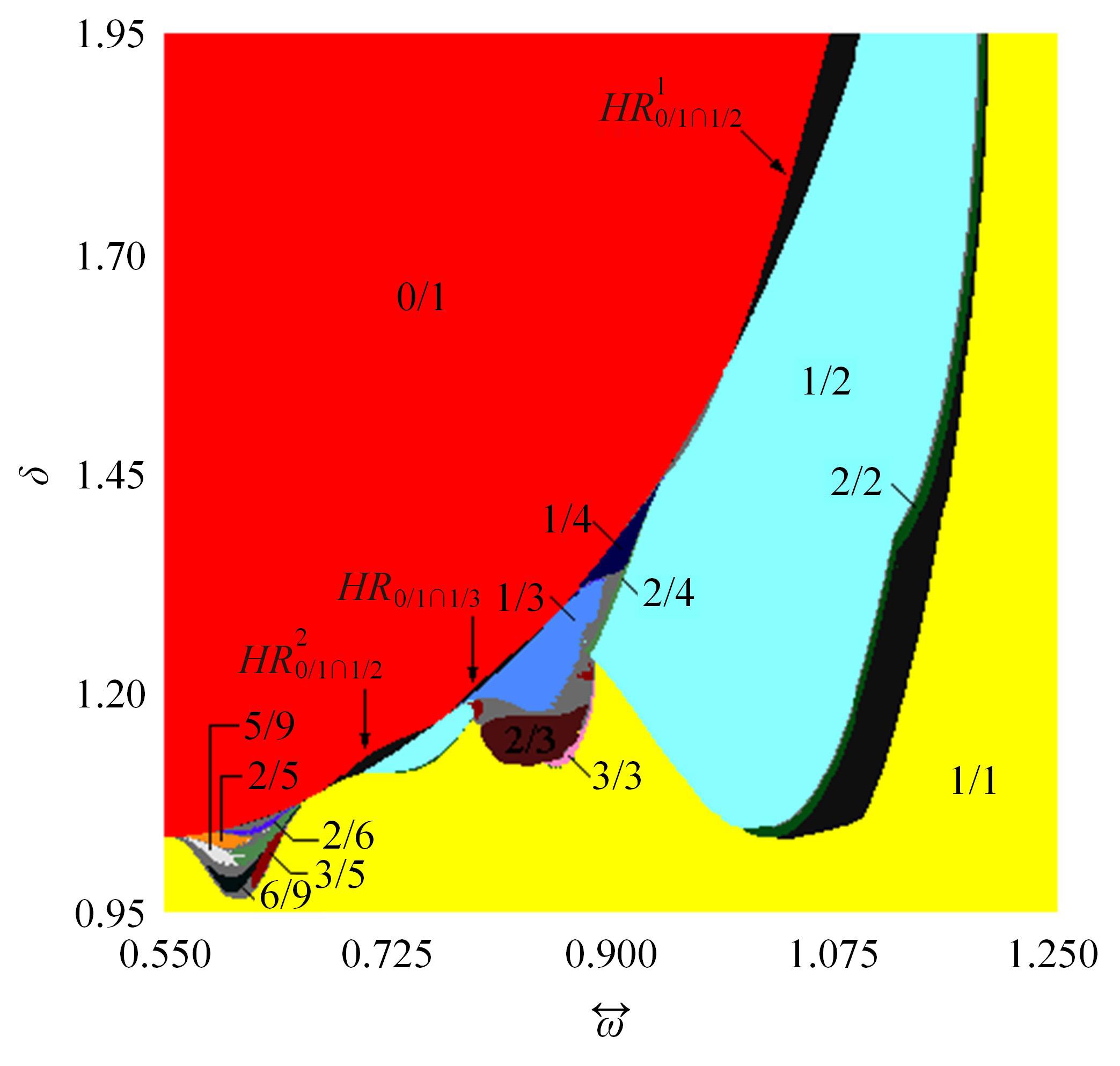
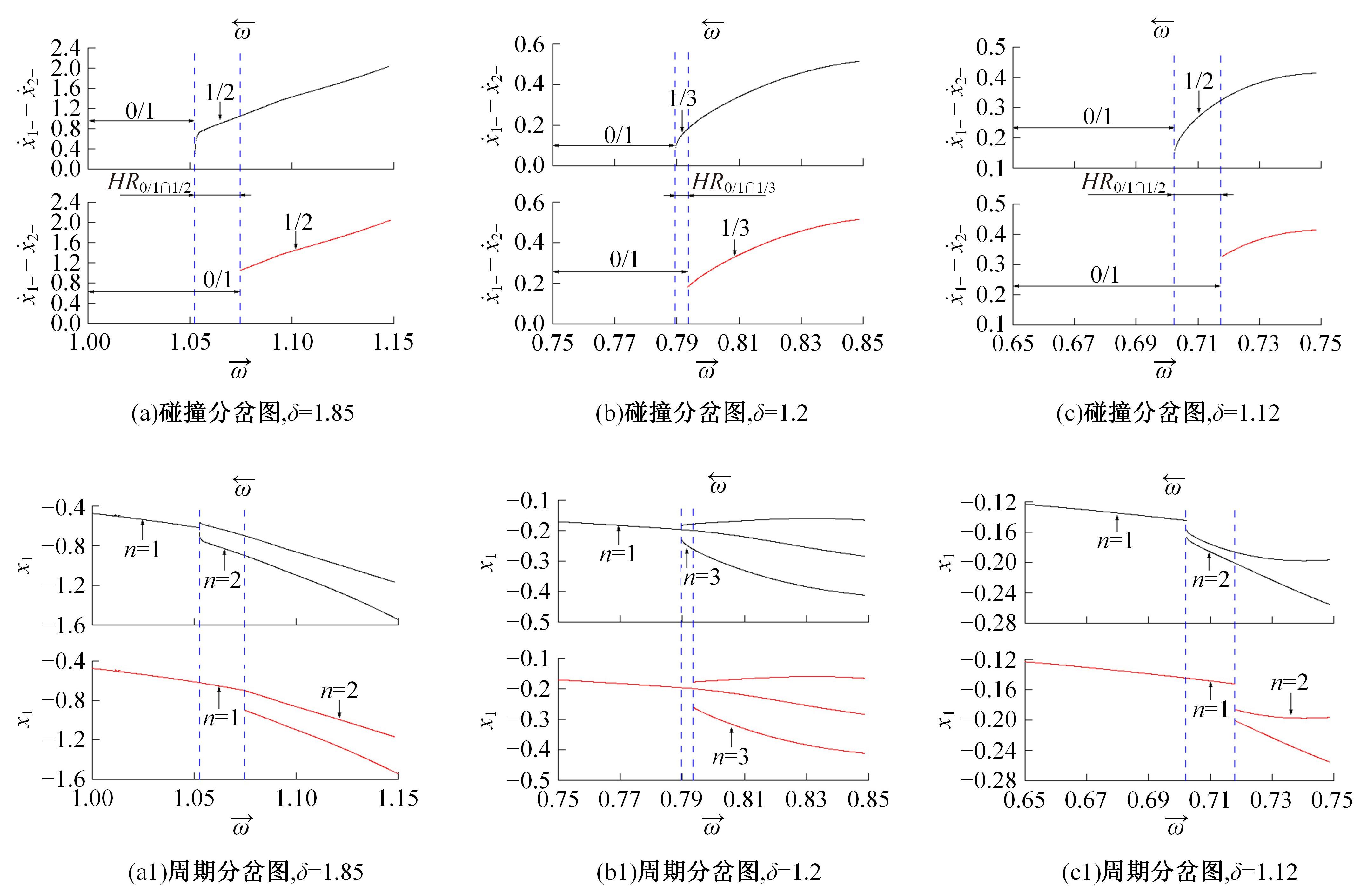
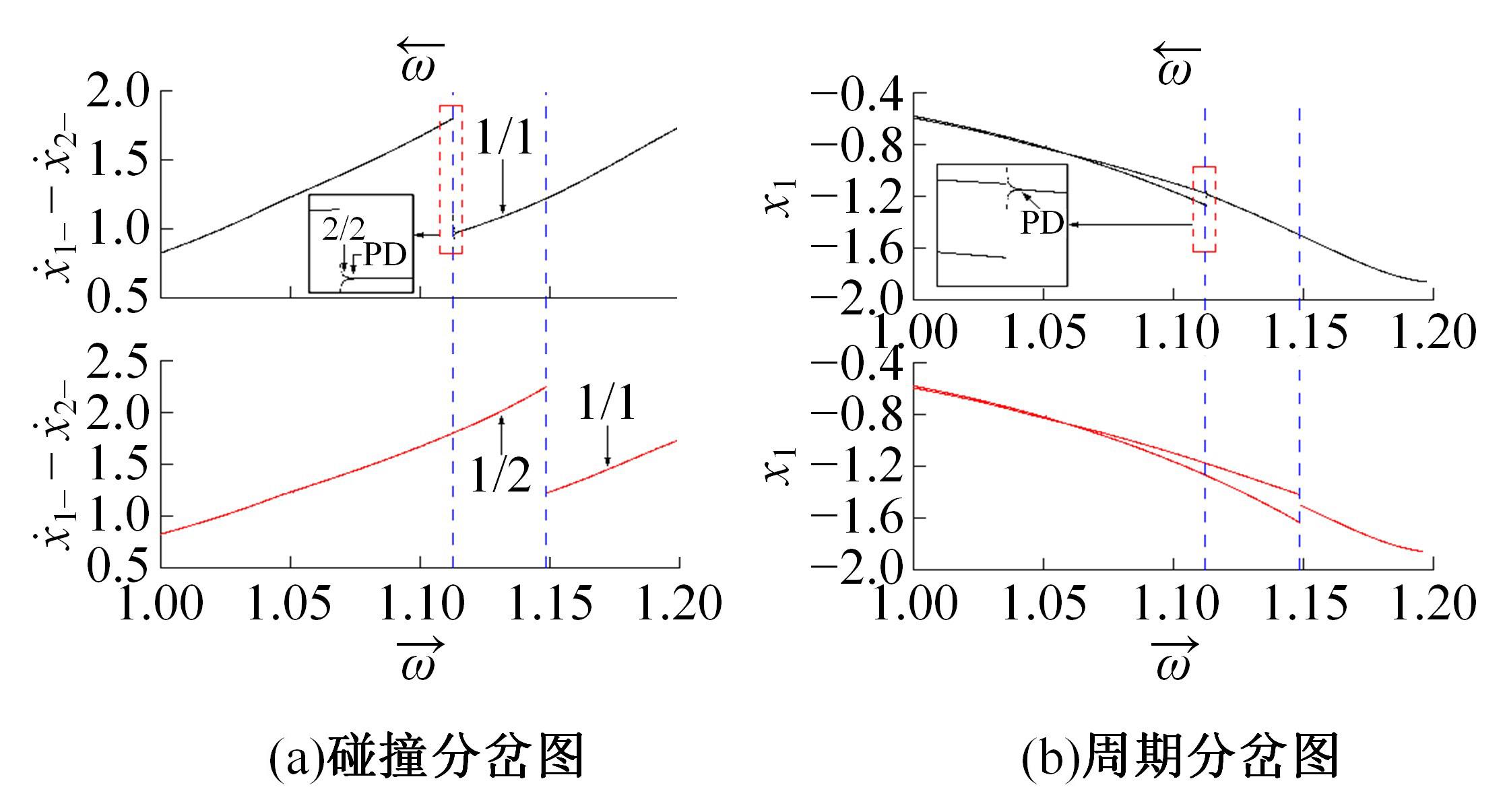
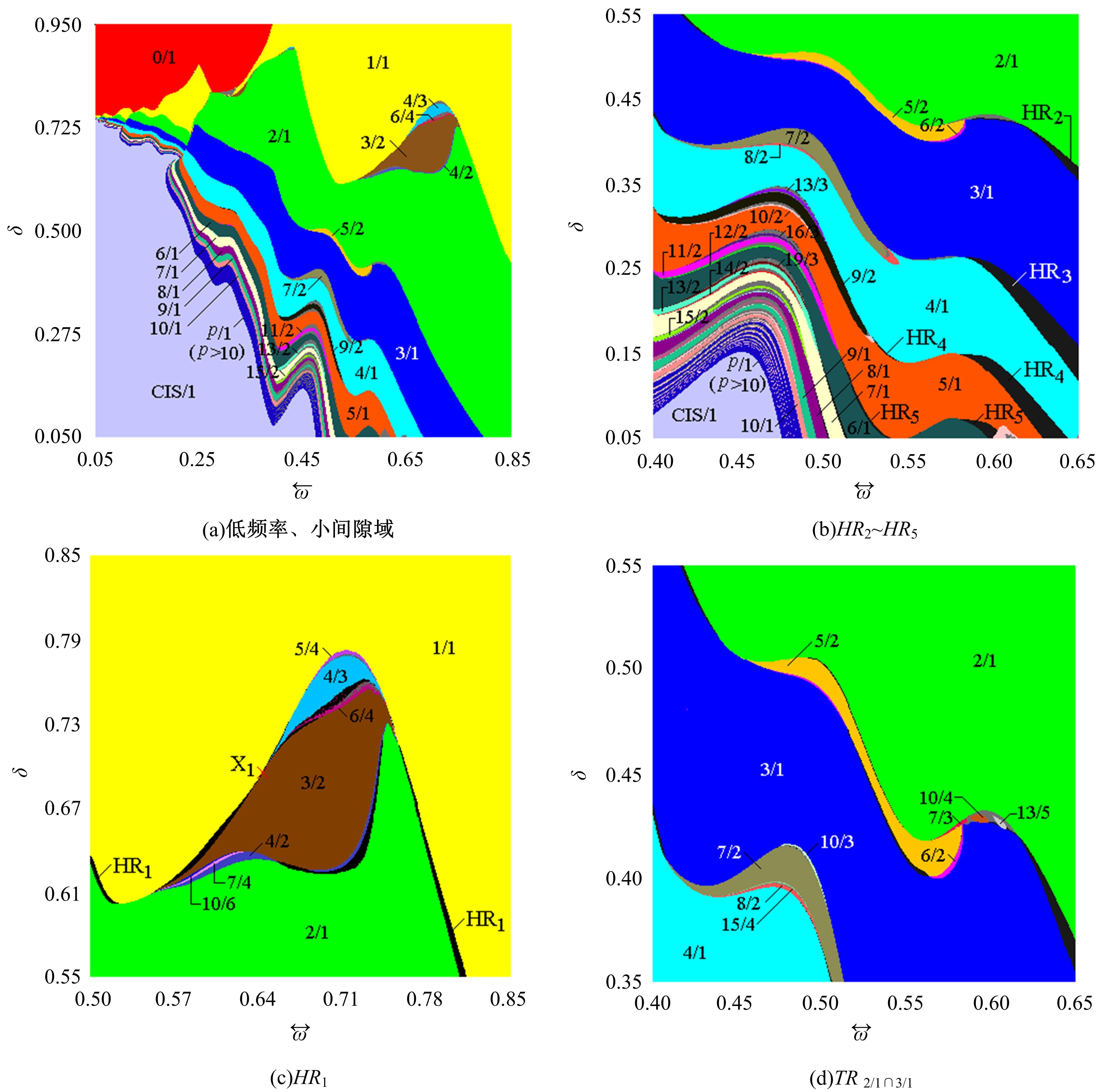
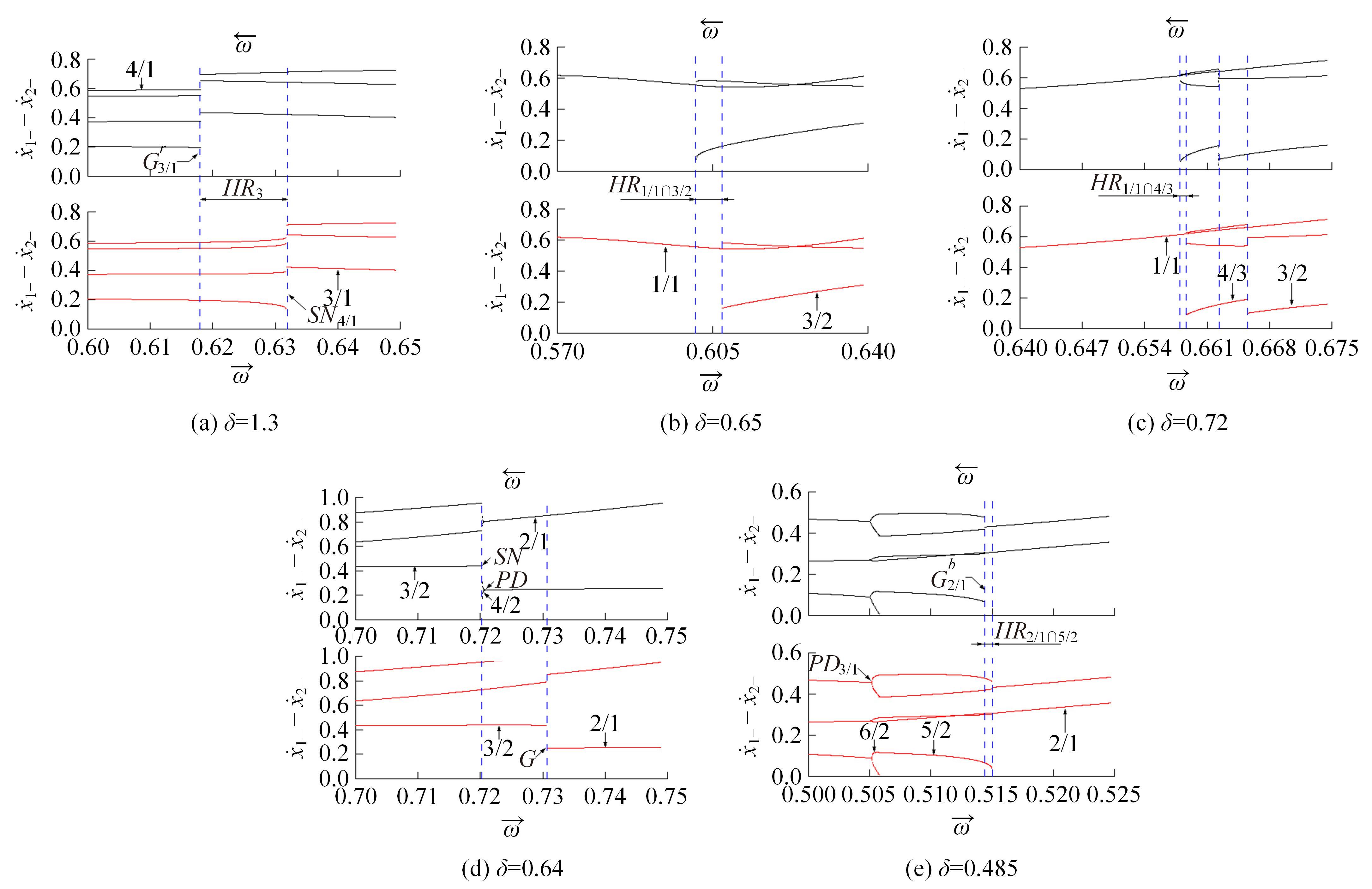
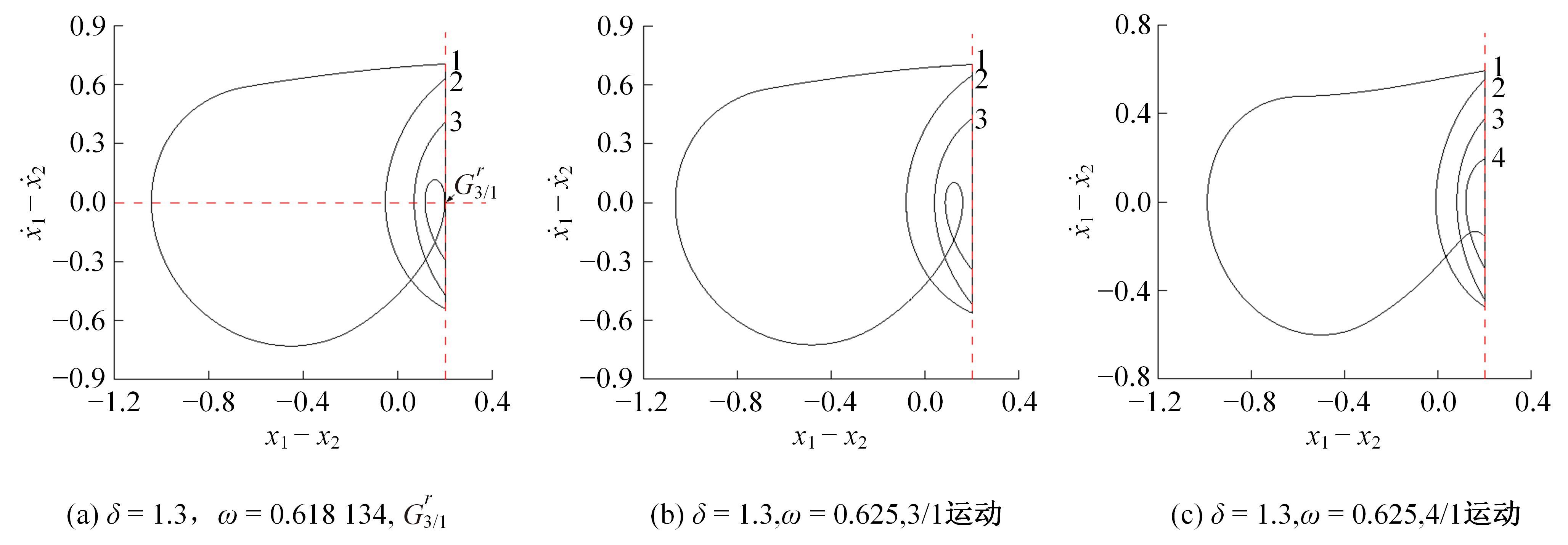
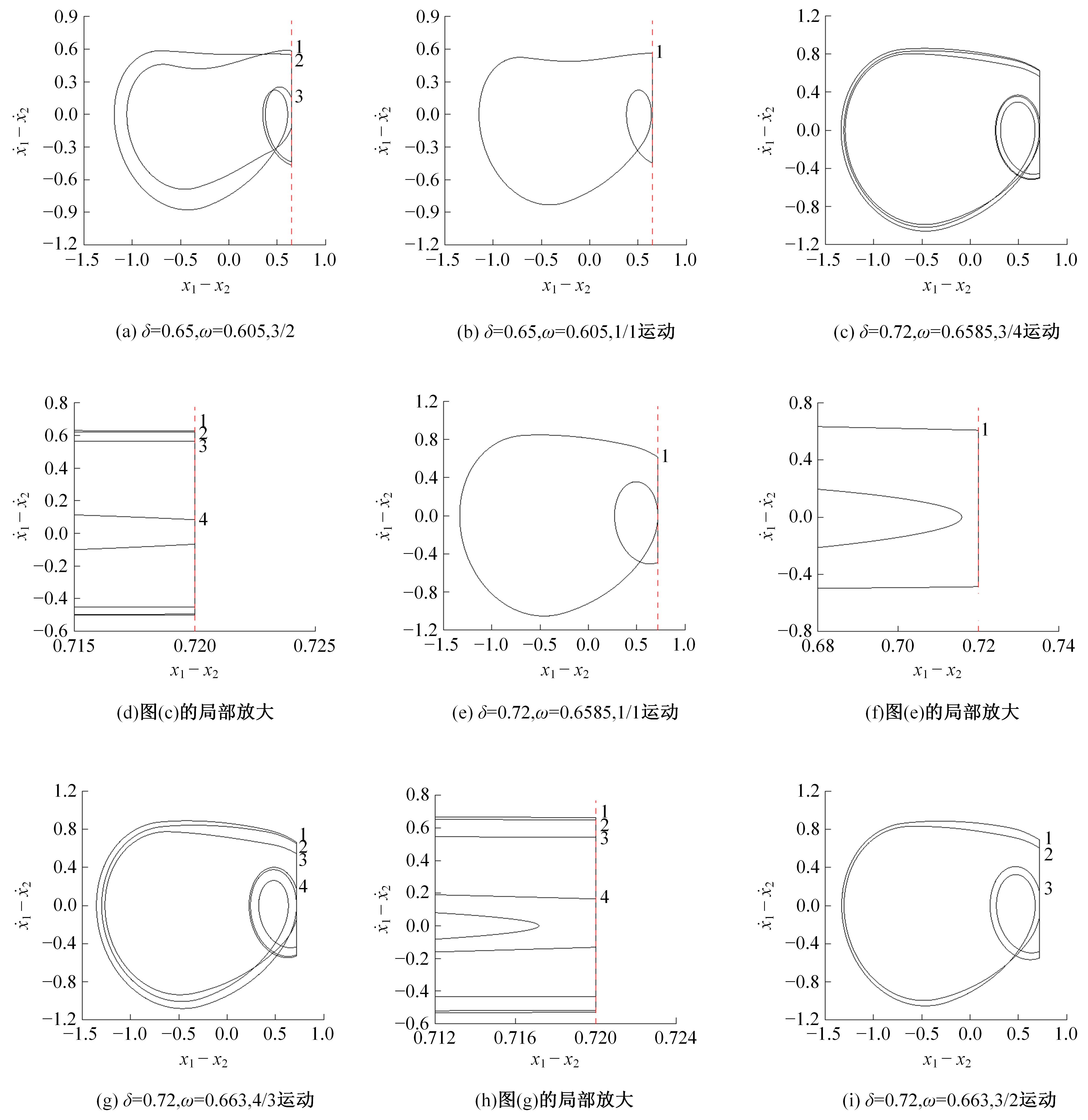
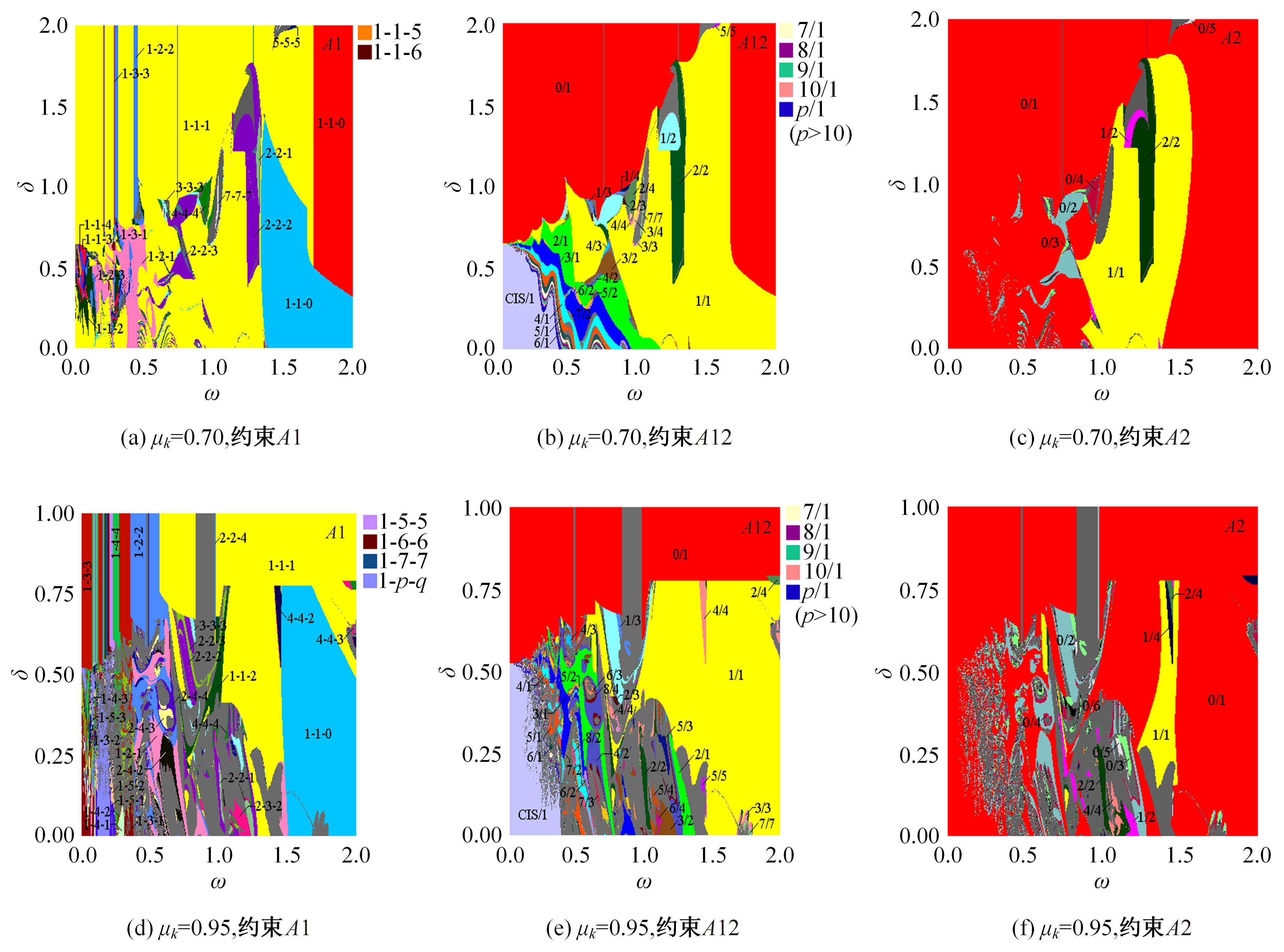
研究了一类含刚性及弹性复合约束的两自由度受迫振动系统,基于双参数协同仿真的数值计算方法,在关键参数激振力频率和两质块间间隙值构成的参数平面上获得了系统周期运动的模式类型和存在区域;揭示了无冲击振动和相邻基本周期冲击振动之间、相邻基本周期运动之间的转迁规律;分析了弹性约束刚度变化对系统周期运动模式类型和存在区域的影响。结果表明:无冲击振动和相邻基本周期运动之间、相邻基本周期运动之间都存在两类主要的转迁区域,包括舌状域和迟滞域;舌状域中包含具有规律性的亚谐运动,这些亚谐运动和相邻的基本周期运动在舌状域边界线附近构成迟滞域群;增大弹性约束处的刚度值,会使得双参数平面中低频率域的概周期运动、混沌运动存在域显著增大,并分割周期运动存在域。
中图分类号:
- O322
| 1 | Shaw S W, Holmes P J. A periodically forced piecewise linear oscillator[J]. Journal of Sound and Vibration, 1983, 90(1): 129-155. |
| 2 | Nordmark A B. Non-periodic motion caused by grazing incidence in an impact oscillator[J]. Journal of Sound and Vibration, 1991, 145(2): 279-297. |
| 3 | Whiston G S. Singularities in vibro-impact dynamics [J]. Journal of Sound and Vibration, 1992, 152(3): 427-460. |
| 4 | Hu H Y. Detection of grazing orbits and incident bifurcations of a forced continuous, piecewise-linear oscillator[J]. Journal of Sound and Vibration, 1994, 187(3): 485-493. |
| 5 | Foale S, Bishop S R. Bifurcations in impact oscillations[J]. Nonlinear Dynamics, 1994, 6: 285-99. |
| 6 | Phanikrishna T, Harry D. Continuous and discontinuous grazing bifurcations in impacting oscillators[J]. Physica D: Nonlinear Phenomena, 2006, 214(2): 187-197. |
| 7 | Levitas J, Weller T, Singer J. Poincaré-like simple cell mapping for non-linear dynamical systems[J]. Journal of Sound and Vibration, 1994, 176(5): 641-662. |
| 8 | Levitas J, Weller T. Poincare linear interpolated cell mapping: method for global analysis of oscillating systems[J]. Journal of Applied Mechanics, 1995, 62(2): 489-495. |
| 9 | 石建飞,张艳龙,王丽,等. Duffing系统的双参数分岔与全局特性分析[J]. 噪声与振动控制,2016(6): 32-37. |
| Shi Jian-fei, Zhang Yan-long, Wang Li, et al. Double-parameter bifurcation and global characteristic analysis of Duffing systems[J]. Noise and Vibration Control, 2016(6):32-37. | |
| 10 | Shi J F, Zhang Y L, Gou X F. Bifurcation and evolution of a forced and damped Duffing system in two-parameter plane[J]. Nonlinear Dynamics, 2018, 93(2):749-766. |
| 11 | Ing J, Pavlovskaia E, Wiercigroch M, et al. Bifurcation analysis of an impact oscillator with a one-sided elastic constraint near grazing[J]. Physica D: Nonlinear Phenomena, 2010, 239(6): 312-321. |
| 12 | Liao M L, Ing J, Chávez J P, et al. Bifurcation techniques for stiffness identification of an impact oscillator[J]. Communications in Nonlinear Science and Numerical Simulation, 2016, 41:19-31. |
| 13 | Jiang H B, Antonio S E C, Yoshisuke U, et al. Grazing-induced bifurcations in impact oscillators with elastic and rigid constraints[J]. International Journal of Mechanical Sciences, 2017,127:204-214. |
| 14 | Liu P F, Zhu L Y, Gou X F, et al. Neighboring periodic motion in spur gear pair and its identification methods[J]. Nonlinear Dynamics, 2021, 106: 2991-3023. |
| 15 | 苟向锋,朱凌云,陈代林,等.参数耦合对单自由度直齿圆柱齿轮系统动态特性影响分析[J]. 振动工程学报,2017, 30(2): 202-213. |
| Gou Xiang-feng, Zhu Ling-yun, Chen Dai-lin, et al. Analysis of effect of parameters coupling on the dynamic characteristics of a single degree-of-freedom spur gear system[J]. Journal of Vibration Engineering, 2017,30(2): 202-213. | |
| 16 | Gou X F, Zhu L Y, Chen D L. Bifurcation and chaos analysis of spur gear pair in two-parameter plane[J]. Nonlinear Dynamics, 2015, 79(3): 2225-2235. |
| 17 | Zhang Y X, Xie X P, Luo G W. Multiple nested basin boundaries in nonlinear driven oscillators[J]. Communications in Nonlinear Science and Numerical Simulation, 2017, 44: 220-228. |
| 18 | Saunders B E, Vasconcellos R, Kuether R J, et al. Characterization and interaction of geometric and contact/impact nonlinearities in dynamical systems[J]. Mechanical Systems and Signal Processing, 2022, 167(A):No.108481. |
| 19 | Czolczynski K, Blazejczyk-Okolewska B, Okolewski A. Analytical and numerical investigations of stable periodic solutions of the impacting oscillator with a moving base[J]. International Journal of Mechanical Sciences, 2016, 115/116: 325-338. |
| 20 | Li G F, Wu S P, Wang H B, et al. Global behavior of a simplified model for the micro-vibration molding machine in parameter-state space[J]. Mechanism and Machine Theory, 2020, 154:No.104039. |
| 21 | Luo G W, Lyu X H, Zhu X F, et al. Diversity and transition characteristics of sticking and non-sticking periodic impact motions of periodically forced impact systems with large dissipation[J]. Nonlinear Dynamics, 2018, 94: 1047-1079. |
| 22 | 石建飞,苟向锋,张艳龙.两自由度减振镗杆系统的安全盆侵蚀与分岔[J].振动与冲击,2018,37(22): 238-244. |
| Shi Jian-fei, Gou Xiang-feng, Zhang Yan-long. Erosion and bifurcation of the safe basin of a two-degree- of-freedom damping boring bar system[J]. Journal of Vibration and Shock, 2018, 37(22): 238-244. |
| [1] | 孙伟,杨俊. 等角贴敷压电分流片圆柱壳有限元建模及减振分析[J]. 吉林大学学报(工学版), 2024, 54(2): 365-374. |
| [2] | 胡斌,蔡一全,罗昕,毛自斌,李俊伟,郭孟宇,王剑. 基于种群胁迫的有限齿侧空间高速充种理论与试验[J]. 吉林大学学报(工学版), 2024, 54(2): 574-588. |
| [3] | 王佳怡,刘昕晖,王展,陈晋市,韩亚方,王禹琪. 基于AMESim的恒流量控制阀流量特性分析[J]. 吉林大学学报(工学版), 2023, 53(9): 2499-2507. |
| [4] | 程亚兵,杨泽宇,李岩,安立持,徐泽辉,曹鹏宇,陈璐翔. 基于混合动力汽车正时齿形链系统的振动噪声特性[J]. 吉林大学学报(工学版), 2023, 53(9): 2465-2473. |
| [5] | 黄贤振,孙楷铂,栾晓刚,胡兵. 螺栓预紧连接可靠性灵敏度分析[J]. 吉林大学学报(工学版), 2023, 53(8): 2219-2226. |
| [6] | 杨艳,侍玉青,张晓蓉,罗冠炜. 一类多刚性限幅振动系统的动态稳定性分析[J]. 吉林大学学报(工学版), 2023, 53(2): 364-375. |
| [7] | 宋剑锋,黄鑫磊,仪帅,杨振熙,董永刚,李树林. 列车制动过程踏面温度场及应力⁃应变分布特性[J]. 吉林大学学报(工学版), 2023, 53(10): 2773-2784. |
| [8] | 刘洋. 动臂塔机防后倾缓冲力计算方法[J]. 吉林大学学报(工学版), 2023, 53(10): 2785-2794. |
| [9] | 刘洋. 动臂塔机卸载冲击仿真及试验[J]. 吉林大学学报(工学版), 2022, 52(6): 1292-1300. |
| [10] | 程亚兵,陈璐翔,葛平玉,杨泽宇,曹鹏宇. 双相正时套筒链的动力学仿真分析及磨损失效[J]. 吉林大学学报(工学版), 2022, 52(4): 781-788. |
| [11] | 张朋成,彭斌,张宇波. 基于圆渐开线建立变截面涡旋齿的方法与理论[J]. 吉林大学学报(工学版), 2022, 52(4): 789-798. |
| [12] | 赵洋,肖洋,孙皓,霍文浩,冯松,廖勇. 基于围道积分的润滑接触齿轮微点蚀损伤特征模拟[J]. 吉林大学学报(工学版), 2022, 52(4): 799-810. |
| [13] | 张龙,徐天鹏,王朝兵,易剑昱,甄灿壮. 基于卷积门控循环网络的齿轮箱故障诊断[J]. 吉林大学学报(工学版), 2022, 52(2): 368-376. |
| [14] | 郑伟,孙见君,马晨波,於秋萍,张玉言,牛韬. 汽车轮毂加工夹具的研究现状及展望[J]. 吉林大学学报(工学版), 2022, 52(1): 25-36. |
| [15] | 田晓超,王海刚,王虎,王志聪,赵剑,杨志刚,吴越. 悬臂式压电振子宽频发电装置设计及测试[J]. 吉林大学学报(工学版), 2021, 51(6): 1953-1958. |
|
||