吉林大学学报(工学版) ›› 2025, Vol. 55 ›› Issue (5): 1772-1779.doi: 10.13229/j.cnki.jdxbgxb.20230791
基于原子范数最小化的极化敏感阵列二维波达方向估计算法
- 1.哈尔滨工程大学 信息与通信工程学院,哈尔滨 150001
2.中国电子科技集团公司 第五十四研究所,石家庄 050081
Two-dimensional DOA estimation algorithm for polarization-sensitive arrays based on atomic norm minimization
Tao CHEN1( ),Min-xing LI1,Li-peng ZHAO2
),Min-xing LI1,Li-peng ZHAO2
- 1.College of Information and Communication Engineering,Harbin Engineering University,Harbin 150001,China
2.The 54th Research Institute of CETC,Shijiazhuang 050081,China
摘要:
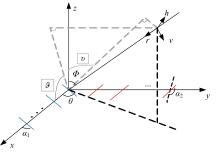
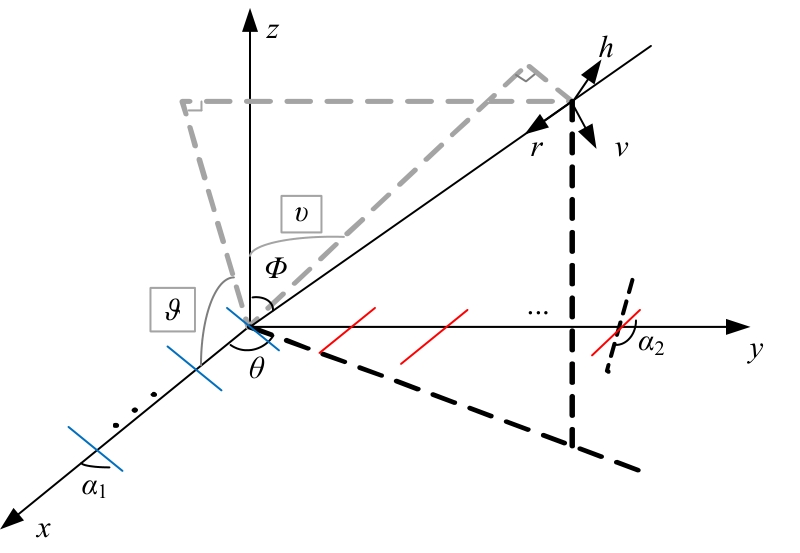
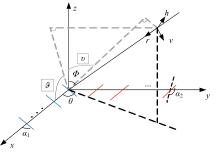
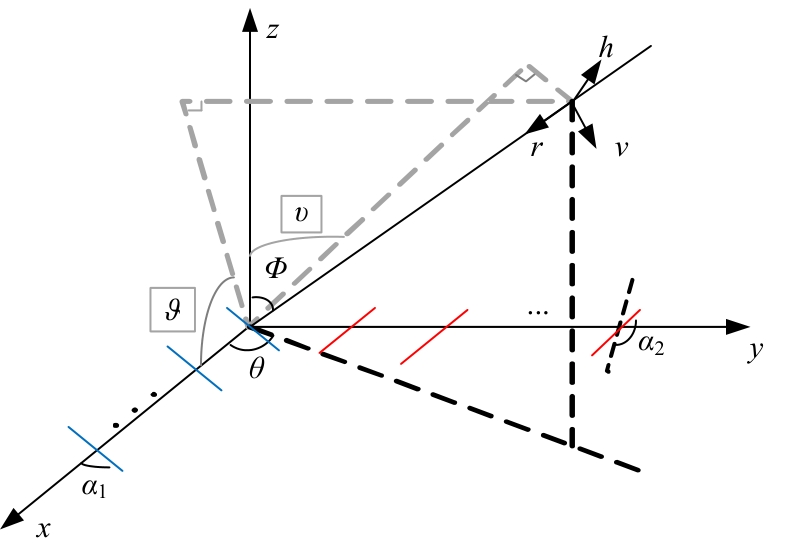
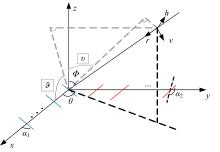
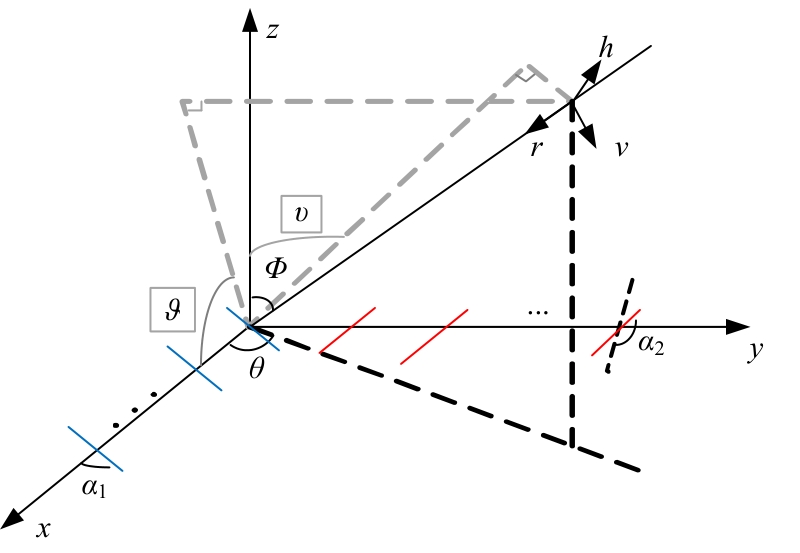
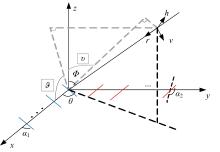
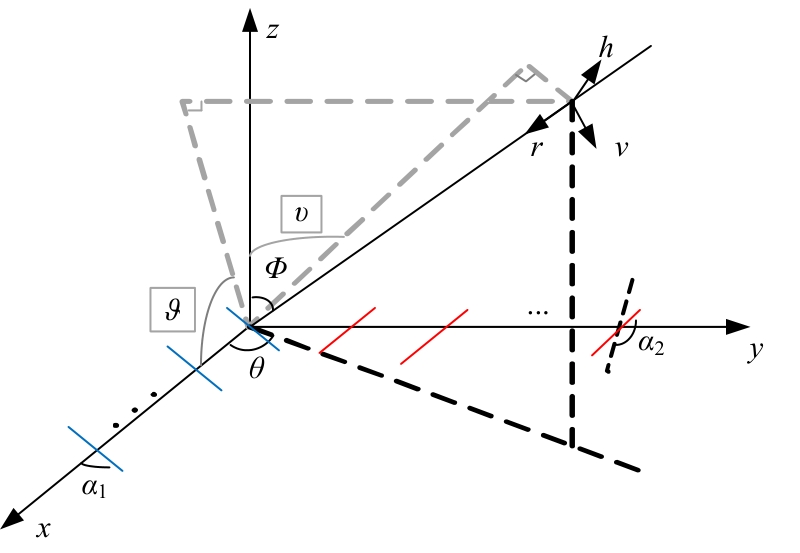
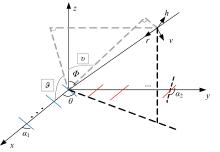
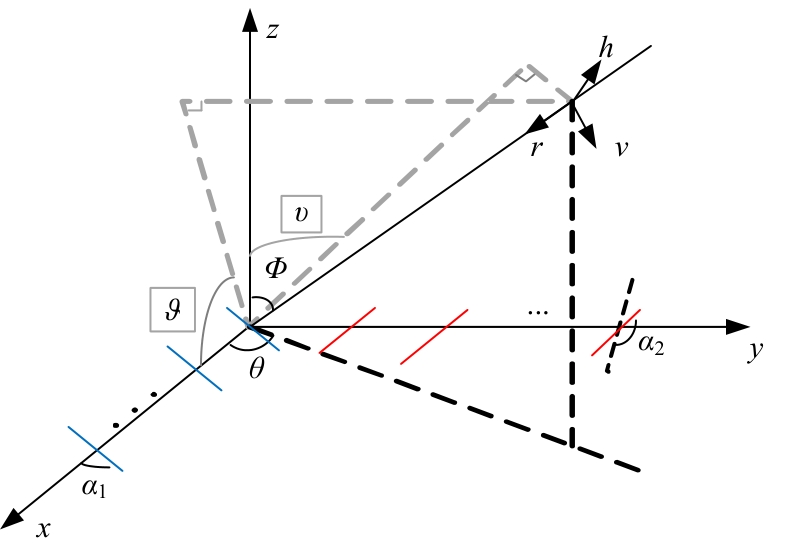
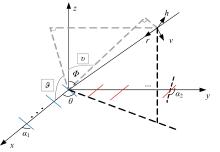
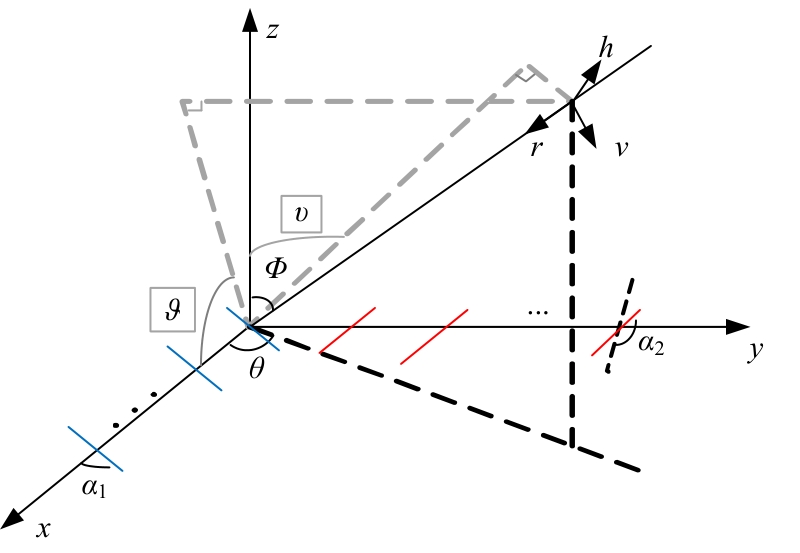
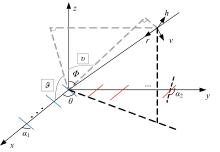
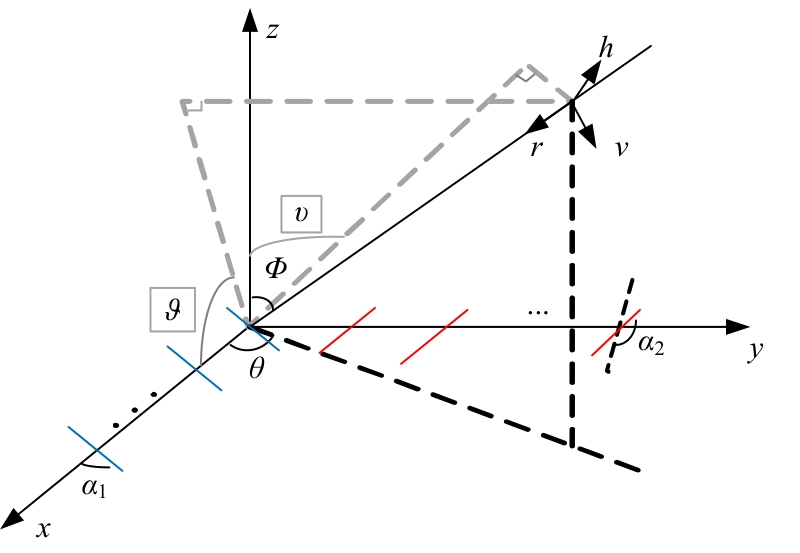
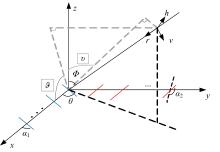
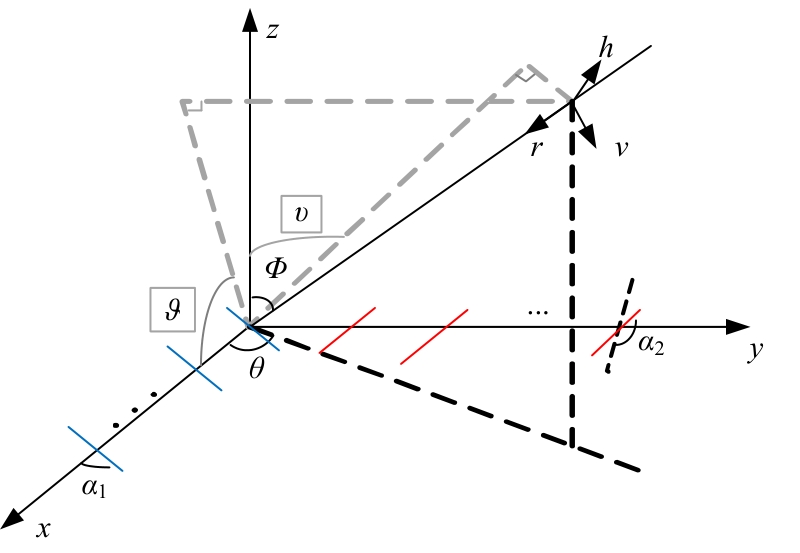
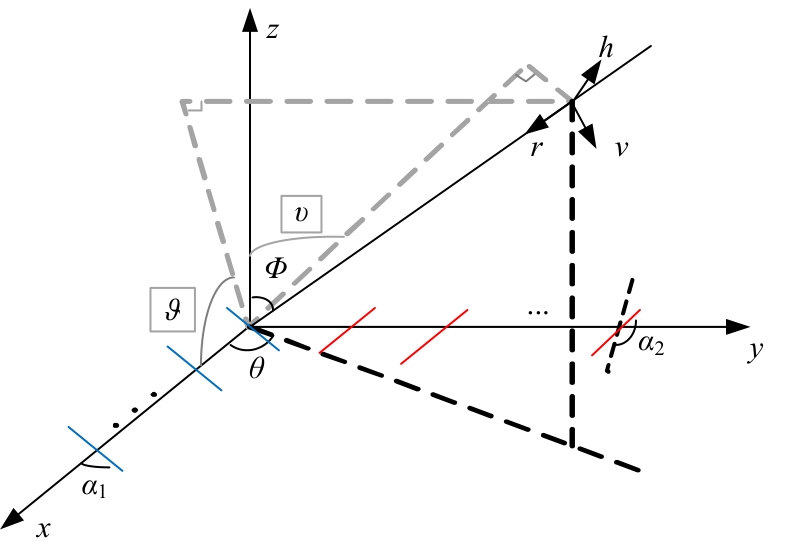
为解决极化敏感阵列中压缩感知类波达方向(DOA)估计算法产生的网格失配带来估计精度下降的问题,本文针对单偶极子阵列在原子范数最小化(ANM)理论的基础上提出一种二维DOA和极化参数的联合估计算法。首先,利用正交极化敏感阵列的特性,分别构造不同极化方向的接收模型,并证明该模型可以消除极化参数的影响,符合ANM模型。其次,通过求解半正定规划问题得到一个半正定的Toeplitz矩阵,随后基于矩阵束算法恢复DOA信息;最后,利用DOA信息和广义特征值理论恢复出极化参数。通过仿真实验验证了本文算法的有效性和优越性。
中图分类号:
- TN911.7
| [1] | Ferrara E, Parks T. Direction finding with an array of antennas having diverse polarizations[J]. IEEE Transactions on Antennas and Propagation, 1983, 31(2): 231-236. |
| [2] | He Z, Tian Z, Zhou M, et al. DOA estimation method for polarization sensitive circular array based on reduced-dimensional MUSIC[C]∥IEEE International Symposium on Antennas and Propagation and USNC-URSI Radio Science Meeting, Denver, USA, 2022: 427-428. |
| [3] | Roy R, Kailath T. ESPRIT-estimation of signal parameters via rotational invariance techniques[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1989, 37(7): 984-995. |
| [4] | Li J, Compton R T. Angle and polarization estimation using ESPRIT with a polarization sensitive array[J]. IEEE Transactions on Antennas and Propagation, 1991, 39(9): 1376-1383. |
| [5] | Tian Y, Sun X, Zhao S. Sparse-reconstruction-based direction of arrival, polarization and power estimation using a cross-dipole array[J]. IET Radar, Sonar & Navigation, 2015, 9(6): 727-731. |
| [6] | Chalise B K, Zhang Y D, Himed B. Compressed sensing based joint DOA and polarization angle estimation for sparse arrays with dual-polarized antennas[C]∥IEEE Global Conference on Signal and Information Processing, Anaheim, USA, 2018: 251-255. |
| [7] | 王洪雁, 于若男, 潘勉, 等. 基于协方差矩阵重构的离网格DOA估计方法[J]. 电子与信息学报, 2021, 43(10): 2863-2870. |
| Wang Hong-yan, Yu Ruo-nan, Pan Mian, et al. Off-grid DOA estimation method based on covariance matrix reconstruction[J]. Journal of Electronics & Information Technology, 2021, 43(10): 2863-2870. | |
| [8] | 陈涛,赵立鹏,史林.基于有限新息率的正交偶极子阵列信号参数估计算法[J].电子与信息学报,2022,44(7):2469-2477. |
| Chen Tao, Zhao Li-peng, Shi Lin. Signal parameter estimation algorithm for orthogonal dipole array based on finite rate of innovation[J]. Journal of Electronics & Information Technology, 2022,44(7):2469-2477. | |
| [9] | Hu B, Shen X Y, Jiang M, et al. Off-grid DOA estimation based on compressed sensing on multipath environment[J]. International Journal of Antennas and Propagation, 2023, 1: 9315869. |
| [10] | Tang G, Bhaskar B N, Shah P, et al. Compressed sensing off the grid[J]. IEEE Transactions on Information Theory, 2013, 59(11): 7465-7490. |
| [11] | Pan Y, Yao M, Luo G Q . et al. Underdetermined direction-of-arrival estimation with coprime array via atomic norm minimization[J]. Radio Engineering, 2020, 29(2): 405-413. |
| [12] | Yang Z, Xie L, Stoica P. Vandermonde decomposition of multilevel toeplitz matrices with application to multi-mensional super-resolution[J]. IEEE Transactions on Information Theory, 2016, 62(6): 3685-3701. |
| [13] | Zhang X, Zheng Z, Wang W Q.DOA estimation of coherent sources using coprime array via atomic norm minimization[J]. IEEE Signal Processing Letters, 2022, 29: 1312-1316. |
| [14] | Wu Y, Wakin M B, Gerstoft P. Gridless DOA estimation with multiple frequencies[J]. IEEE Transactions on Signal Processing, 2023, 71: 417-432. |
| [15] | Wagner M, Park Y, Gerstoft P. Gridless DOA estimation and root-music for non-uniform linear arrays[J]. IEEE Transactions on Signal Processing, 2021, 69: 2144-2157. |
| [16] | 陈涛,李敏行,郭立民.基于原子范数最小化的极化敏感阵列DOA估计[J].电子学报,2023,51(4):835-842. |
| Chen Tao, Li Min-xing, Guo Li-min. DOA estimation of polarization sensitive array based on atomic norm minimization[J]. Acta Electronica Sinica, 2023,51(4):835-842. | |
| [17] | Zhang Z, Wang Y, Tian Z. Efficient two-dimensional line spectrum estimation based on decoupled atomic norm minimization[J]. Signal Processing, 2019, 163: 95-106. |
| [1] | 聂为之,尹斐,苏毅珊. 任务驱动下成像声呐水下目标识别方法综述[J]. 吉林大学学报(工学版), 2025, 55(4): 1163-1175. |
| [2] | 窦慧晶,谢东旭,郭威,邢路阳. 基于改进的正交匹配跟踪算法的波达方向估计[J]. 吉林大学学报(工学版), 2024, 54(12): 3568-3576. |
| [3] | 杨青,于明,阎刚. 基于深度频率特征注意力机制的图像去雨方法[J]. 吉林大学学报(工学版), 2024, 54(10): 2952-2962. |
| [4] | 葛动元,向文江,李健,刘恩辰,姚锡凡. 基于机器视觉的电动汽车充电自动定位方法[J]. 吉林大学学报(工学版), 2023, 53(12): 3465-3471. |
| [5] | 石屹然,齐金伟,曲思凝,潘向阳,符麟. 基于几何功率的α噪声的特征指数估计方法[J]. 吉林大学学报(工学版), 2023, 53(10): 3007-3013. |
| [6] | 曾春艳,严康,王志锋,王正辉. 多尺度生成对抗网络下图像压缩感知重建算法[J]. 吉林大学学报(工学版), 2023, 53(10): 2923-2931. |
| [7] | 王春阳,丘文乾,刘雪莲,肖博,施春皓. 基于平面拟合的地面点云精确分割方法[J]. 吉林大学学报(工学版), 2023, 53(3): 933-940. |
| [8] | 周怡娜,董宏丽,张勇,路敬祎. 基于VMD去噪和散布熵的管道信号特征提取方法[J]. 吉林大学学报(工学版), 2022, 52(4): 959-969. |
| [9] | 李雪梅,王春阳,刘雪莲,谢达. 基于SESTH的线性调频连续波激光雷达信号时延估计[J]. 吉林大学学报(工学版), 2022, 52(4): 950-958. |
| [10] | 窦慧晶,丁钢,高佳,梁霄. 基于压缩感知理论的宽带信号波达方向估计[J]. 吉林大学学报(工学版), 2021, 51(6): 2237-2245. |
| [11] | 侯春萍,赵春月,王致芃,田海瑞. 基于有效异常样本构造的视频异常检测算法[J]. 吉林大学学报(工学版), 2021, 51(5): 1823-1829. |
| [12] | 燕学智,王子婷,王昕. 超声波三维定位系统中基线长度与误差传递关系的分析[J]. 吉林大学学报(工学版), 2021, 51(4): 1461-1469. |
| [13] | 李厚杰,王法胜,贺建军,周瑜,李威,窦宇轩. 基于伪样本正则化Faster R⁃CNN的交通标志检测[J]. 吉林大学学报(工学版), 2021, 51(4): 1251-1260. |
| [14] | 李伟,陈剑,陶善勇. 自适应耦合周期势系统随机共振信号增强方法[J]. 吉林大学学报(工学版), 2021, 51(3): 1091-1096. |
| [15] | 刘国华,周文斌. 基于卷积神经网络的脉搏波时频域特征混叠分类[J]. 吉林大学学报(工学版), 2020, 50(5): 1818-1825. |
|