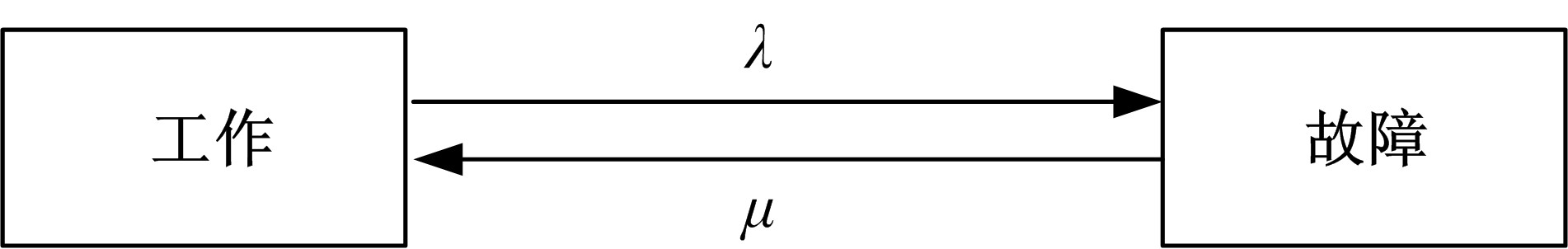吉林大学学报(工学版) ›› 2021, Vol. 51 ›› Issue (2): 697-703.doi: 10.13229/j.cnki.jdxbgxb20191122

• 计算机科学与技术 • 上一篇    

基于马尔可夫过程的风电系统可靠性分析

赵志欣1,2(),唐慧1,刘仁云1()   

  1. 1.长春师范大学 数学学院，长春 130032
    2.吉林大学 数学学院，长春 130012
  • 收稿日期:2019-12-09 出版日期:2021-03-01 发布日期:2021-02-09
  • 通讯作者: 刘仁云 E-mail:jczzx10@163.com;liurenyun2005@163.com
  • 作者简介:赵志欣（1982-），男，副教授，博士.研究方向：可靠性理论.E-mail:jczzx10@163.com
  • 基金资助:
    国家自然科学基金项目(11601040);吉林省科技厅项目(20180101224JC)

Reliability analysis of wind power generation system based on Markov process

Zhi-xin ZHAO1,2(),Hui TANG1,Ren-yun LIU1()   

  1. 1.School of Mathematics，Changchun Normal University，Changchun 130032，China
    2.School of Mathematics，Jilin University，Changchun 130012，China
  • Received:2019-12-09 Online:2021-03-01 Published:2021-02-09
  • Contact: Ren-yun LIU E-mail:jczzx10@163.com;liurenyun2005@163.com

RICH HTML

 6   

PDF (PC)

369

摘要：

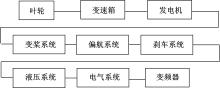
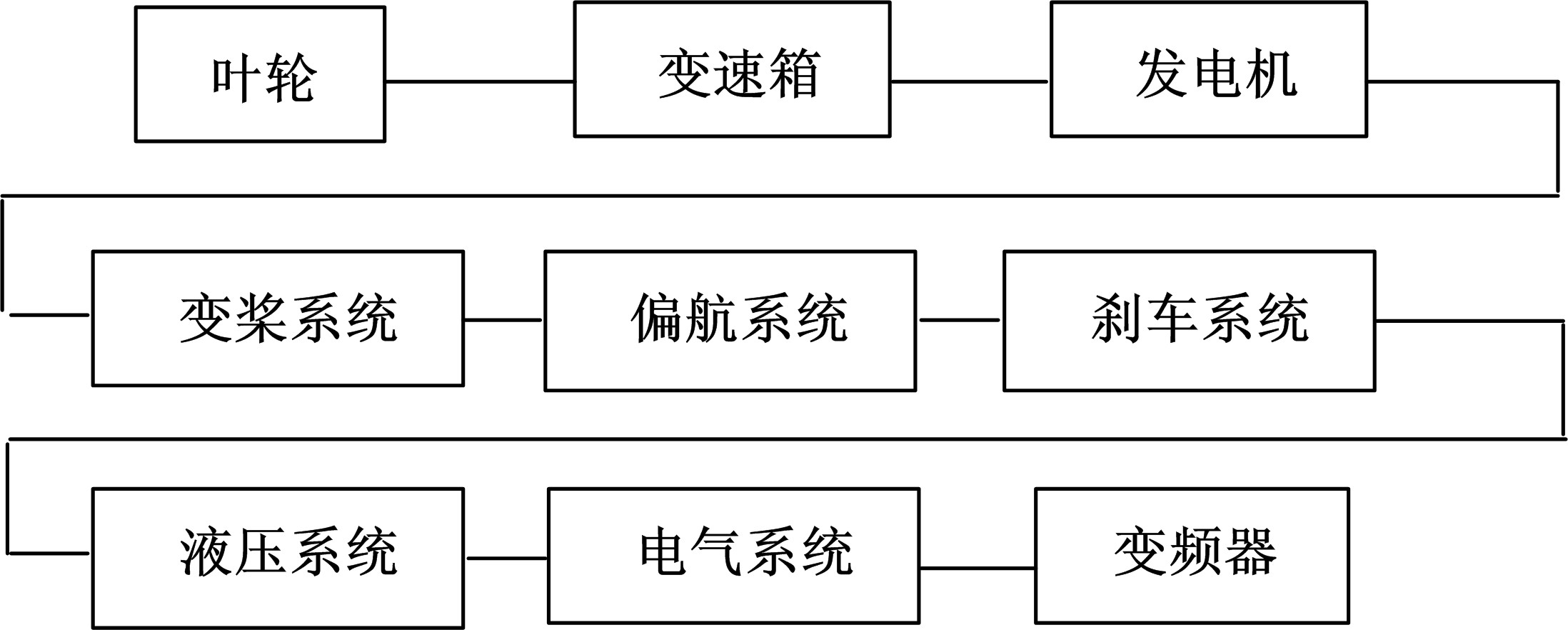
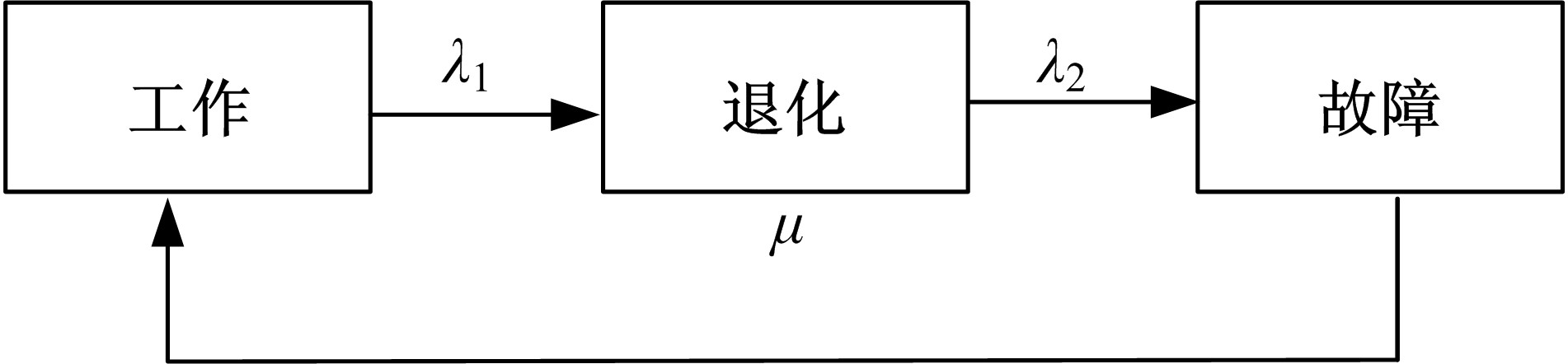
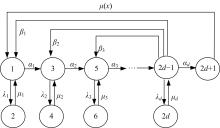
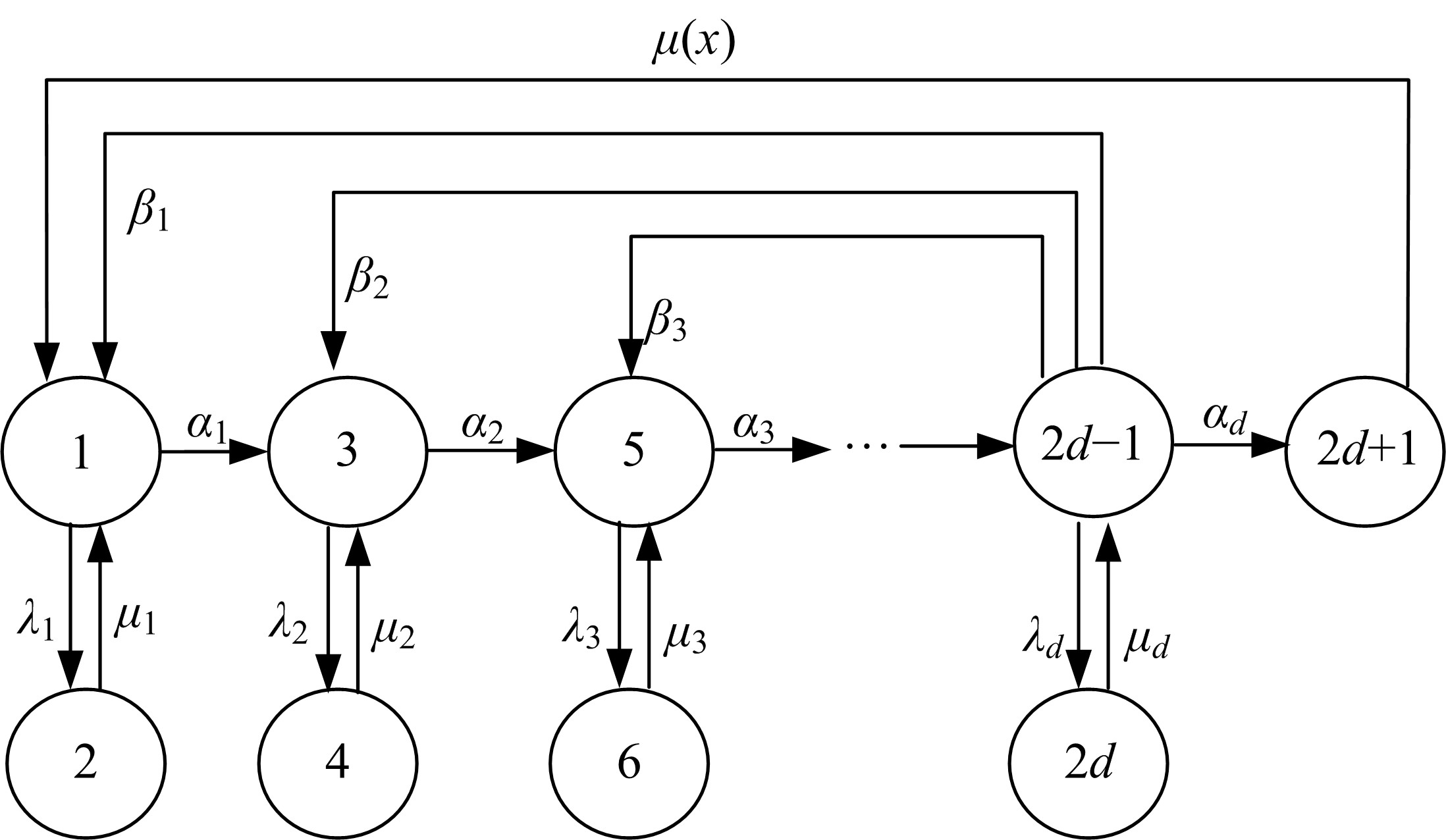
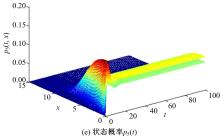
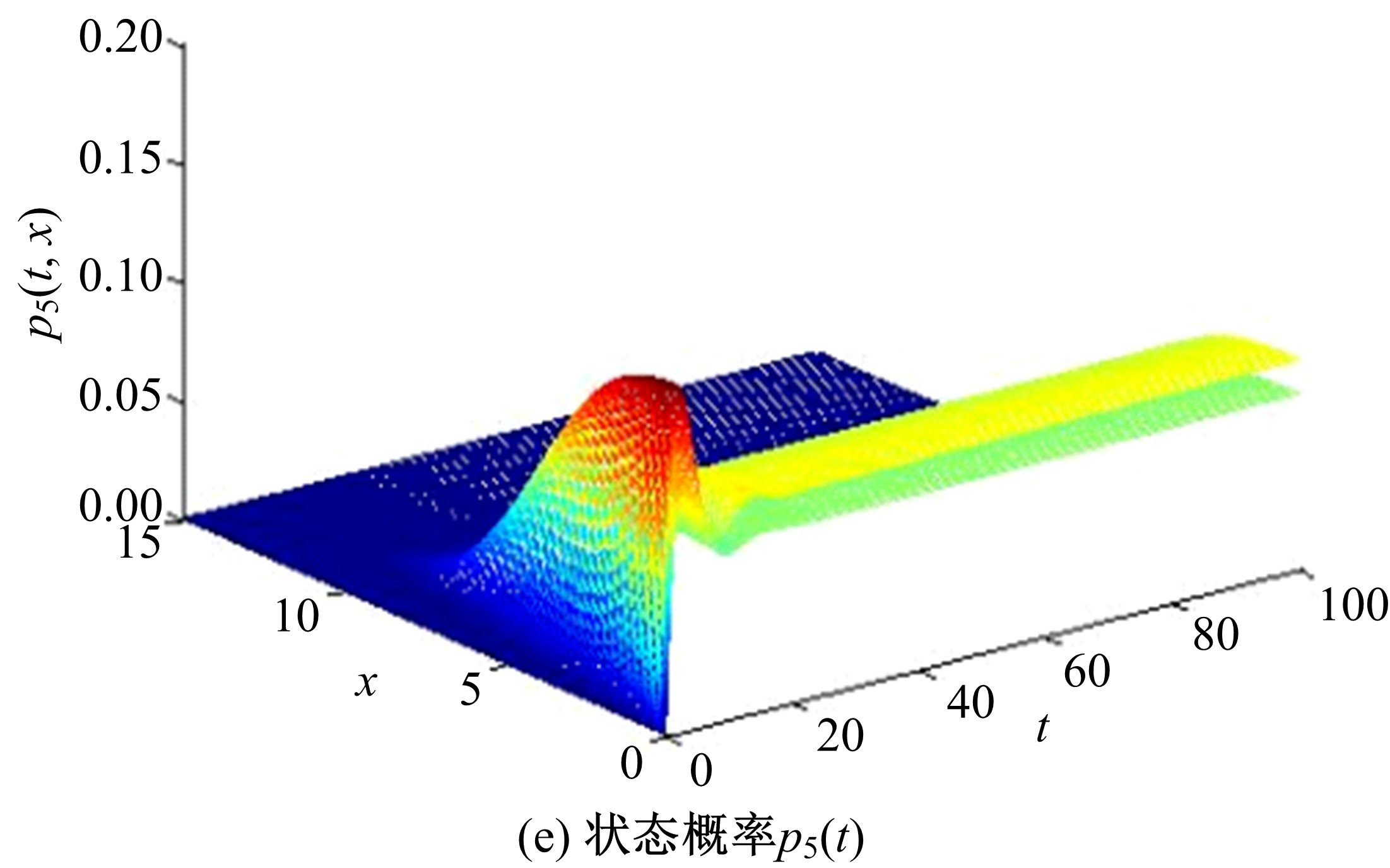
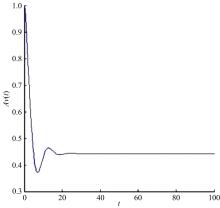
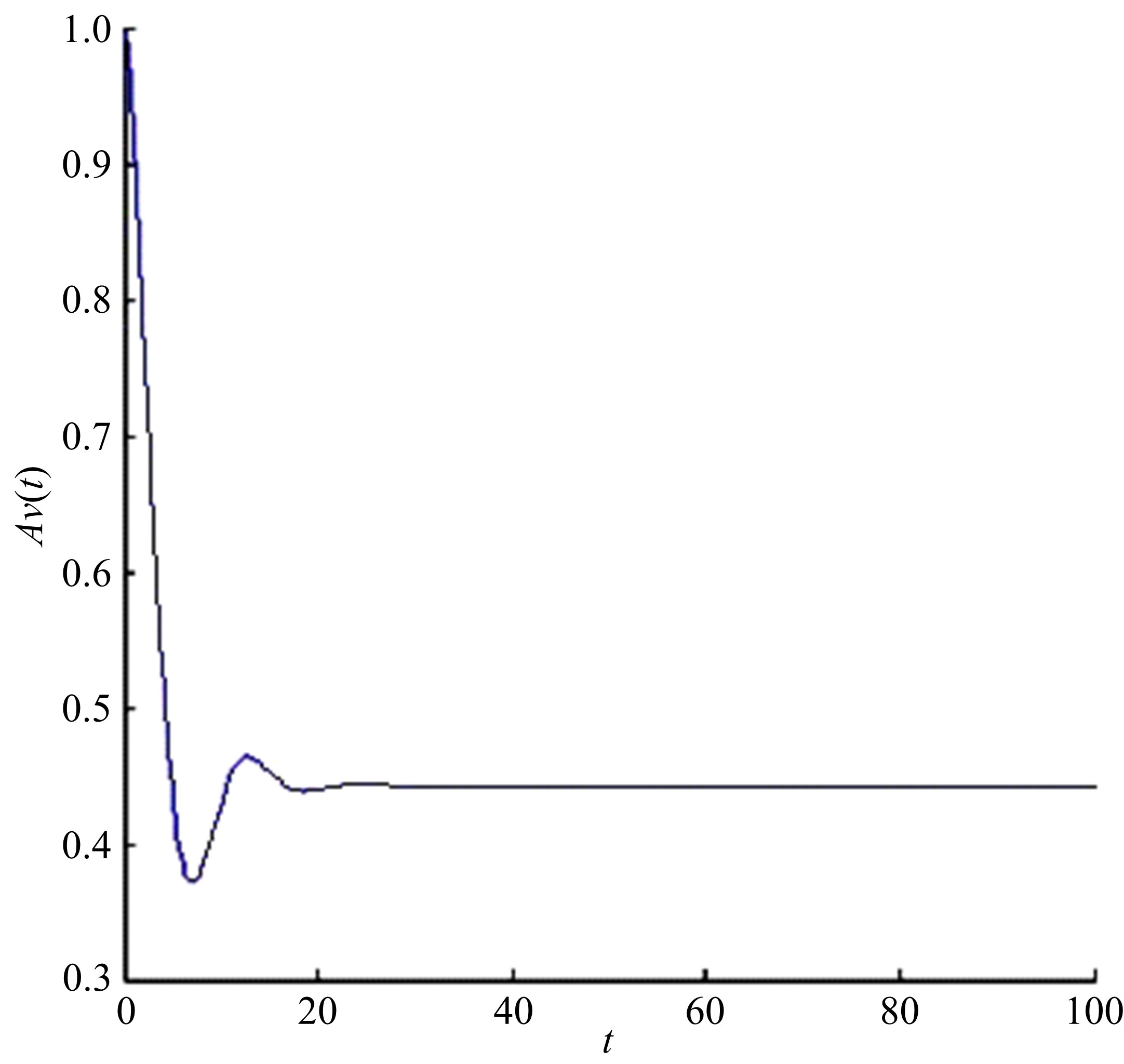
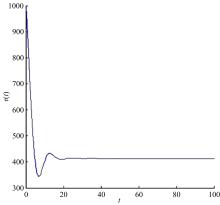
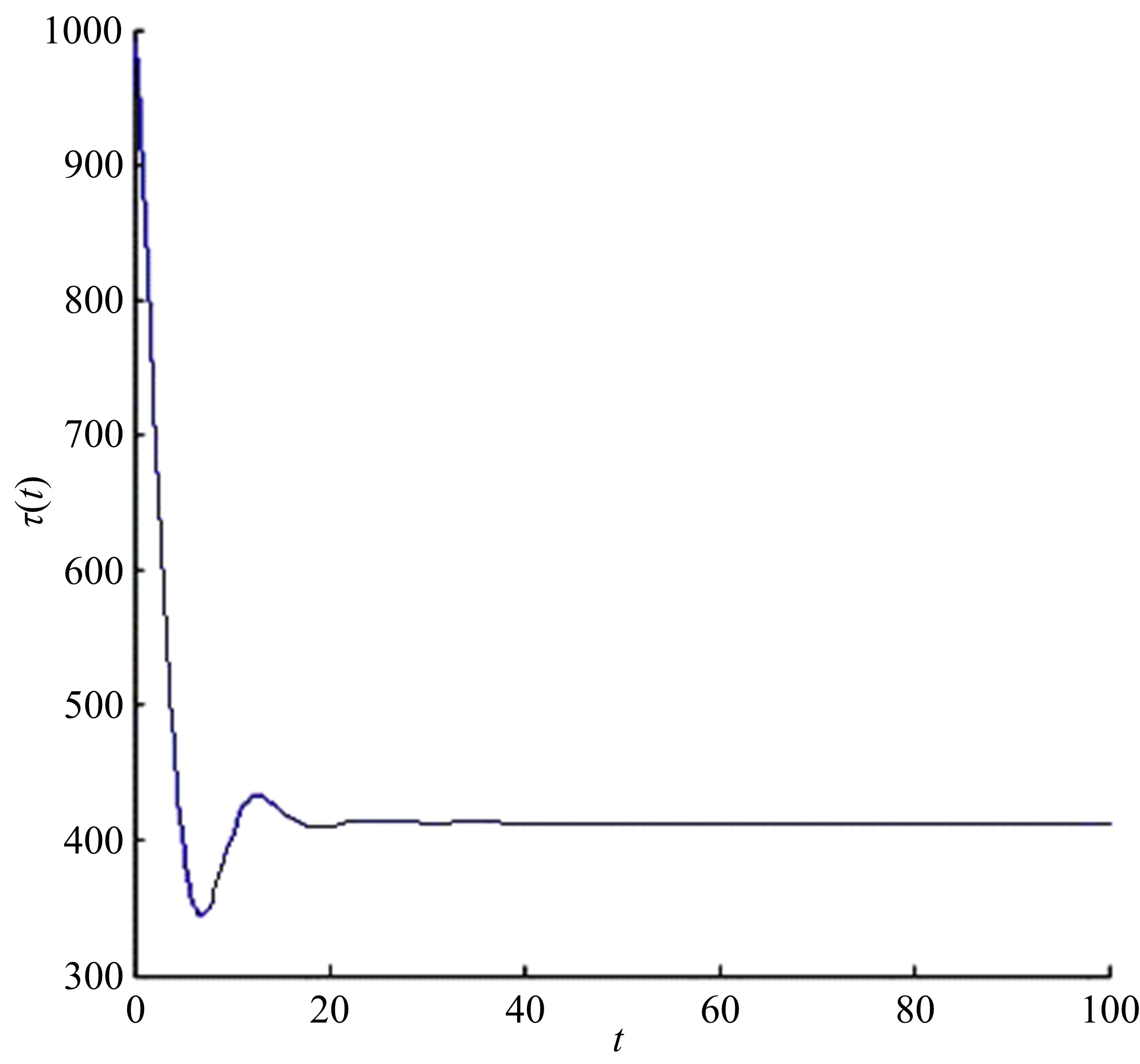
本文讨论了具有多种维修策略的多状态可修退化风电系统。根据风电系统运行环境和原理，利用马尔可夫过程和可靠性理论建立了风电系统的可靠性模型，该风电系统随时间变化可退化成多个离散状态，且系统在功能完好和完全故障之间的多个中间状态相互转化；然后，将该系统转化为一个抽象柯西问题，探讨了该可修退化系统各状态概率的存在唯一性；最后，在能效等级确定的条件下，对该退化系统各状态概率和可用度等指标进行了模拟。研究发现，通过马尔可夫过程可以描述可修退化风电系统，同时利用该模型可以有效地对系统相关可靠性指标进行定量分析。

关键词: 系统工程, 可修系统, 马尔可夫过程, 可用度

Abstract:

This paper discusses a multi-state repairable and degraded wind power generation system with multiple maintenance strategies. According to the operating environment and the principle of wind power generation system， the reliability model of this system is established by using Markov process and reliability theory. This wind power generation system can be degraded into several discrete states over time， and the system can be converted into more intermediate states between the good state and complete failure. Then the system can be transformed into an abstract Cauchy problem， and the existence and uniqueness of the state probabilities of the repairable degenerate system are discussed. Finally， the simulation of the state probability， availability and other indexes of the degradation system was carried out under the determined energy efficiency grade. The study shows that the wind power system can be described by Markov process， and this model can effectively make quantitative analysis of the system reliability index.

Key words: systems engineering, repairable system, Markov process, availability

中图分类号: 

  • TB112

图1

风电机组系统可靠性框图"

图2

两状态可修风电系统状态"

图3

退化风电系统状态"

图4

系统状态转移图"

图5

状态概率"

图6

瞬态可用度Av(t)"

图7

输出性能的τ(t)"

1 李俊峰. 2012中国风电发展报告[M]. 北京: 中国环境科学出版社, 2012.
2 王志新. 海上风力发电技术[M]. 北京: 机械工业出版社, 2012.
3 李飞龙, 林勇刚, 李伟, 等. 风能静液压传动控制技术[J]. 吉林大学学报: 工学版, 2014, 44(6): 1664-1668.
Li Fei-long, Lin Yong-gang, Li Wei, et al. Energy hydraulic transmission system of wind turbine[J]. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(6): 1664-1668.
4 马文星, 刘彬, 刘春宝, 等. 风力发电液力调速系统及其控制[J]. 吉林大学学报: 工学版, 2013, 43(5): 1276-1283.
Ma Wen-xing, Liu Bin, Liu Chun-bao, et al. Hydrodynamic speed adjusting system and its control of wind turbine[J]. Journal of Jilin University (Engineering and Technology Edition), 2013, 43(5): 1276-1283.
5 曲波, 郑阳, 刘大欣. 风电惯性台架模拟惯量的计算[J]. 吉林大学学报: 工学版, 2011, 41(): 155-159.
Qu Bo, Zheng Yang, Liu Da-xin. Calculation of intertia moment about wind turbine test-bed braking system[J]. Journal of Jilin University (Engineering and Technology Edition), 2011, 41(Sup.1): 155-159.
6 Tavner P J, Xiang J, Spinato E. Reliability analysis for wind turbines[J]. Wind Energy, 2007, 10(1): 1-18.
7 Selwyn T S, Kesavan R. Availability analysis of wind turbines and its sub assemblies with markov analysis at uncertain wind[J]. Advanced Science Letters,2013, 19(8): 2210-2214.
8 Florin M, Ciprian N. Availability evaluation of wind as a repairable system[C]∥International Conference on Optimization of Electrical and Electronic Equipment, Romania, 2014: 756-761.
9 Arabian H H, Oraee H, Tavner P J. Wind turbine productivity considering electrical subassembly reliability[J]. Renewable Energy, 2010, 35(1): 190-197.
10 李大字, 冯园园, 刘展, 等. 风力发电机组可靠性建模与维修策略优化[J]. 电网技术, 2011, 35(9): 122-127.
Li Da-zi, Feng Yuan-yuan, Liu Zhan, et al. Reliability modeling and maintenance strategy optimization for wind power generation sets[J]. Power System Technology, 2011, 35(9): 122-127.
11 秦洋, 马慧民, 朱田玮, 等. 风力发电系统可靠性建模与优化检修策略[J]. 电力科学与工程, 2015, 31(7): 53-58.
Qin Yang, Ma Hui-min, Zhu Tian-wei, et al. Reliability modelling and maintenance strategy optimization for wind power system[J]. Electric Power Science and Engineering, 2015, 31(7): 53-58.
12 Byon E, Yu D. Season-dependent condition-based maintenance for a wind turbine using a partially observed Markov decision process[J]. IEEE Transaction on Power System, 2010, 25(4): 1823-1834.
13 张晓红, 曾建潮, 石冠男, 等. 基于退化状态空间划分的风电机组视情维修决策[J]. 控制与决策, 2019, 34(9): 1909-1916.
Zhang Xiao-hong, Zeng Jian-chao, Shi Guan-nan, et al. Optimal decision of condition-based maintenance of wind turbines based on deterioration state-space partition[J]. Control and Decision, 2019, 34(9): 1909-1916.
14 苏春, 周小荃. 基于半马尔科夫决策过程的风力机状态维修优化[J]. 机械工程学报, 2012, 48(2): 44-49.
Su Chun, Zhou Xiao-quan. Condition-based maintenance optimization for wind turbines based on Semi-Markov decision process[J]. Journal of Mechanical Engineering, 2012, 48(2): 44-49.
15 Soro I W, Nourelfath M, Ait-Kadi D. Performance evaluation of multi-state degraded systems with minimal repairs and imperfect preventive maintenance[J]. Reliability Engineering and System Safety, 2010, 95(2): 65-69.
16 霍娟, 唐贵基, 贾桂红, 等. 并网风电机组寿命分布拟合与维修方案评价[J]. 可再生能源, 2016, 34(5): 712-718.
Huo Juan, Tang Gui-ji, Jia Gui-hong, et al. Life distribution fitting and maintenance plan evaluation of grid connected wind turbines[J]. Renewable Energy Resources, 2016, 34(5): 712-718.
17 Rajeevan K, Shouri P V, Nair U. Markov modeling and reliability allocation in wind turbine for availability enhancement[J]. Life Cycle Reliability and Safety Engineering, 2018, 7(3): 147-157.
18 Geni G, Li X Z, Zhu G T. Functional Analysis Method in Queueing Theorem[M]. UK: Research Information Ltd, 2001.
[1] 张健,吴坤润,杨敏,冉斌. 智能网联环境下交叉口双环自适应控制模型[J]. 吉林大学学报(工学版), 2021, 51(2): 541-548.
[2] 王殿海,沈辛夷,罗小芹,金盛. 车均延误最小情况下的相位差优化方法[J]. 吉林大学学报(工学版), 2021, 51(2): 511-523.
[3] 宋现敏,张明业,李振建,王鑫,张亚南. 动态公交专用道的设置及其仿真分析评价[J]. 吉林大学学报(工学版), 2020, 50(5): 1677-1686.
[4] 贾洪飞,丁心茹,杨丽丽. 城市潮汐车道优化设计的双层规划模型[J]. 吉林大学学报(工学版), 2020, 50(2): 535-542.
[5] 尹超英,邵春福,王晓全,熊志华. 考虑空间异质性的建成环境对通勤方式选择的影响[J]. 吉林大学学报(工学版), 2020, 50(2): 543-548.
[6] 张大伟,祝海涛. 考虑行人差异性的人群疏散最优决策理论模型[J]. 吉林大学学报(工学版), 2020, 50(2): 549-556.
[7] 常玉林,袁才鸿,孙超,张鹏. 基于改进元胞传输模型的城市路网实际阻抗计算方法[J]. 吉林大学学报(工学版), 2020, 50(1): 132-139.
[8] 宗长富,文龙,何磊. 基于欧几里得聚类算法的三维激光雷达障碍物检测技术[J]. 吉林大学学报(工学版), 2020, 50(1): 107-113.
[9] 隋振,姜源. 基于MIMO类脑情感学习回路的横-纵向综合控制驾驶员模型[J]. 吉林大学学报(工学版), 2020, 50(1): 140-146.
[10] 别一鸣,姜凯,汤茹茹,王琳虹,熊昕宇. 考虑方案过渡影响的单点交通控制时段划分方法[J]. 吉林大学学报(工学版), 2019, 49(6): 1844-1851.
[11] 谷远利, 张源, 芮小平, 陆文琦, 李萌, 王硕. 基于免疫算法优化LSSVM的短时交通流预测[J]. 吉林大学学报(工学版), 2019, 49(6): 1852-1857.
[12] 程国柱, 冯思鹤, 冯天军. 占用车行道的路内停车泊位设置条件[J]. 吉林大学学报(工学版), 2019, 49(6): 1858-1864.
[13] 龙海波,杨家其,赵学彧. 基于转运延误风险的多方式协同货运载运工具配置优化[J]. 吉林大学学报(工学版), 2019, 49(5): 1492-1499.
[14] 别一鸣,汤茹茹,王运豪,文斌,冯天军,王琳虹. 信号交叉口进口车道饱和流率估计方法[J]. 吉林大学学报(工学版), 2019, 49(5): 1459-1464.
[15] 梁泉,翁剑成,周伟,荣建. 基于关联规则的公共交通通勤稳定性人群辨识[J]. 吉林大学学报(工学版), 2019, 49(5): 1484-1491.
Viewed
Full text


Abstract

Cited
  Shared   
  Discussed   
No Suggested Reading articles found!
版权所有 © 《吉林大学学报(工学版)》编辑部
地址：长春市人民大街5988号　电话：+86-431-85095297　传真：+86-431-85094074　E-mail: xbgxb@jlu.edu.cn
本系统由北京玛格泰克科技发展有限公司设计开发