基于黎曼流形的稀疏图保持投影的特征提取

doi:10.13229/j.cnki.jdxbgxb20200589

摘要/Abstract

摘要：

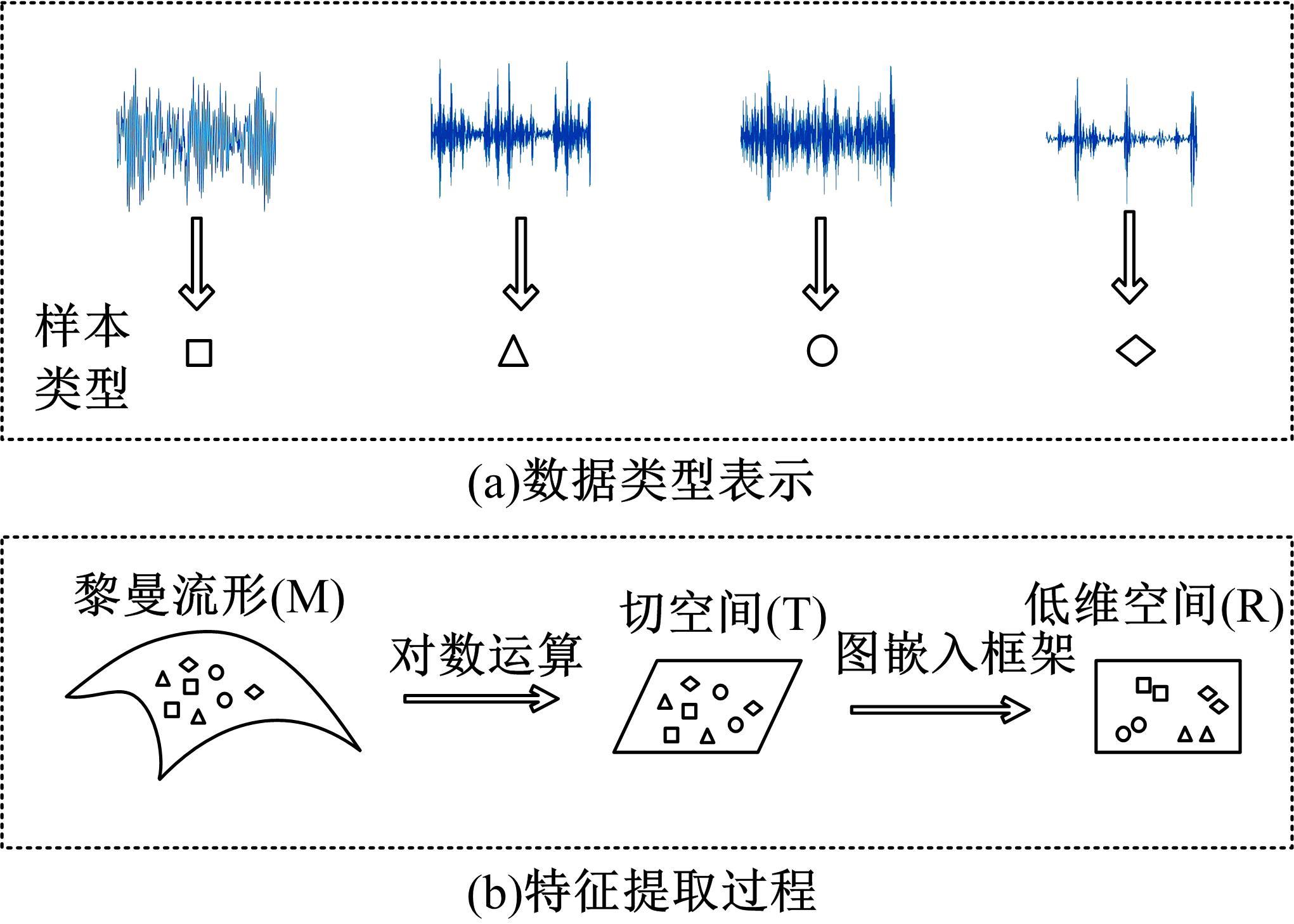
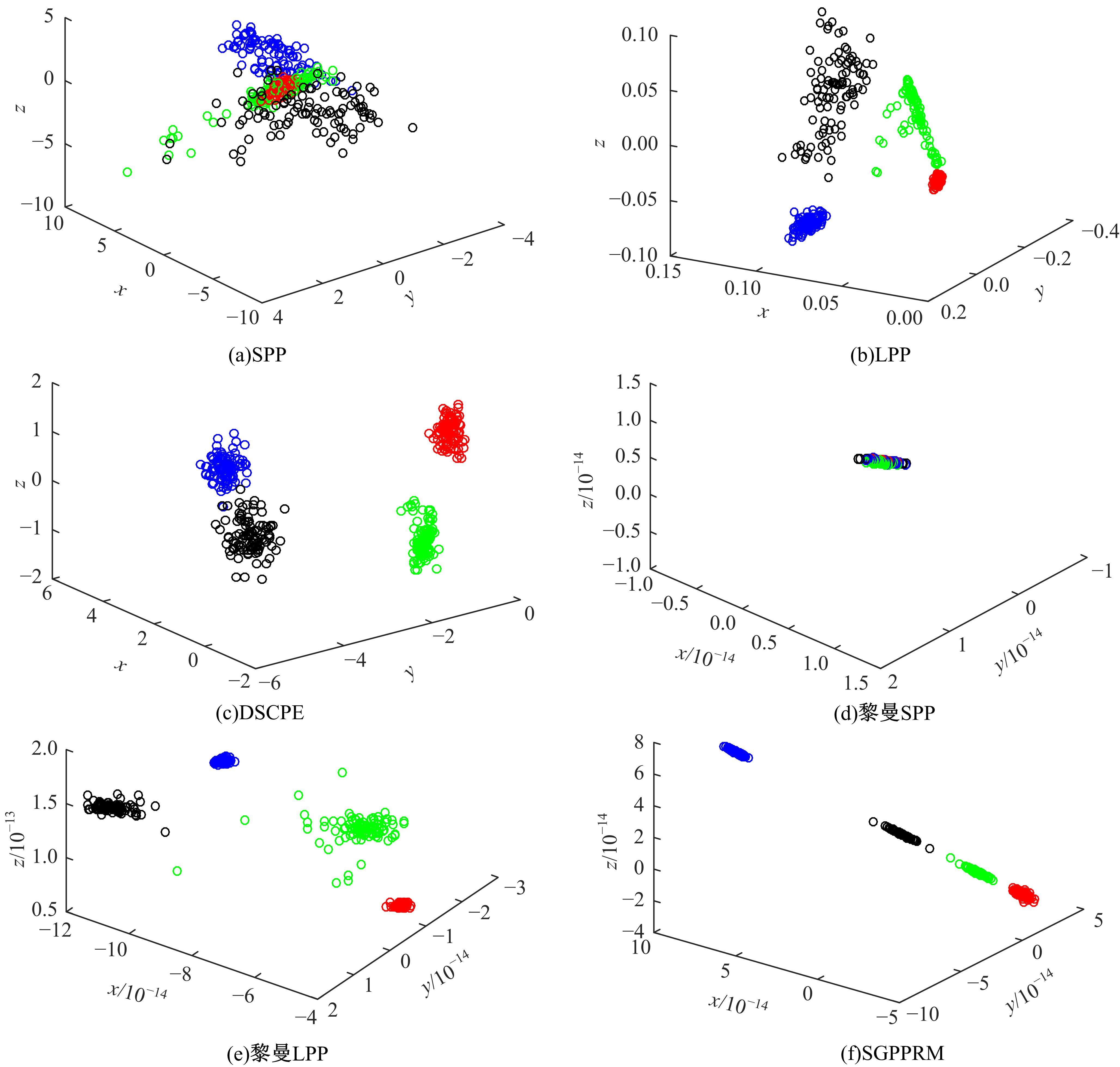
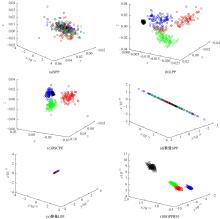
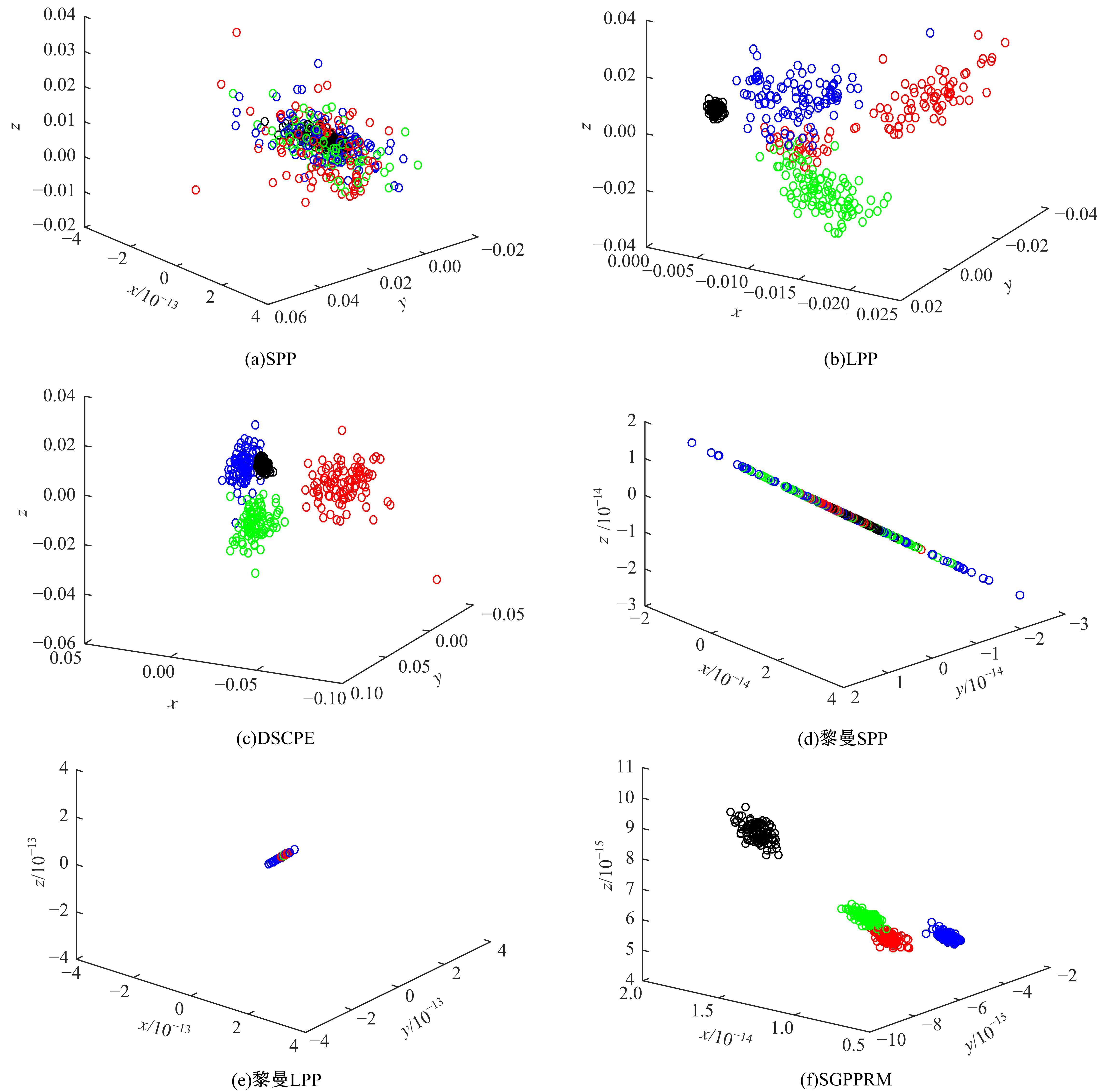
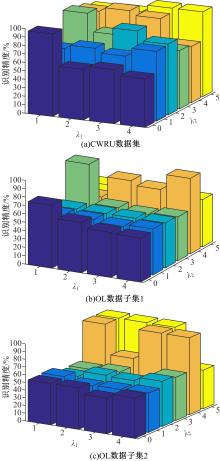
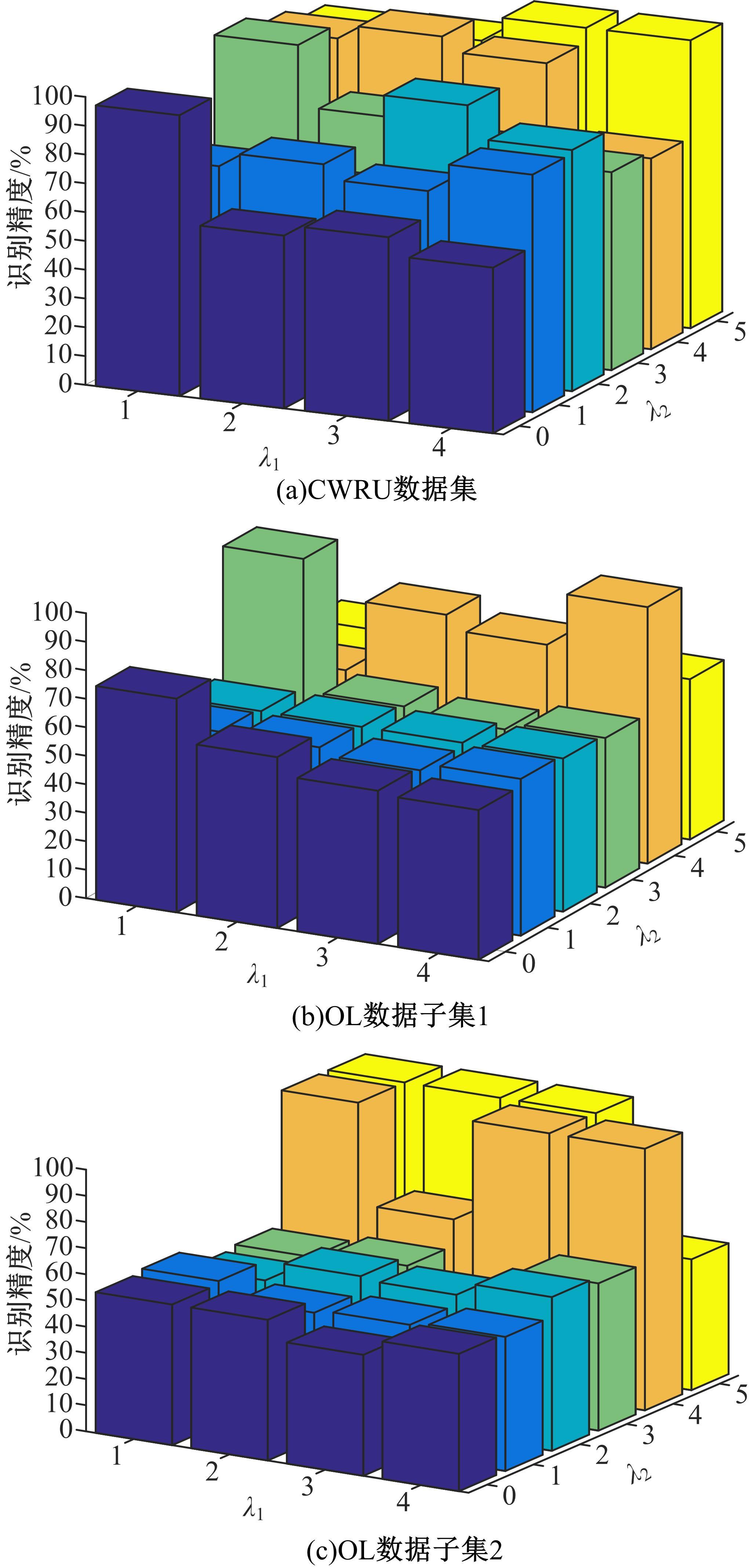
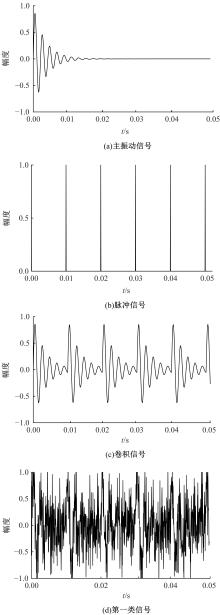
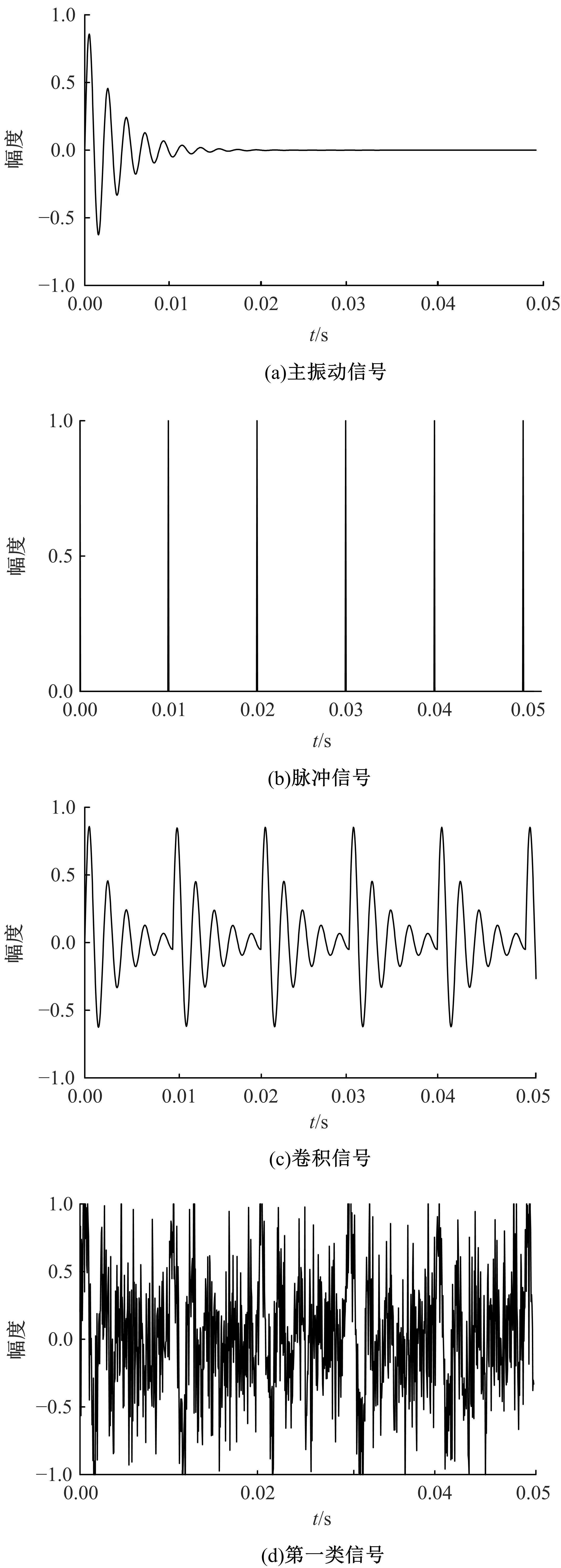
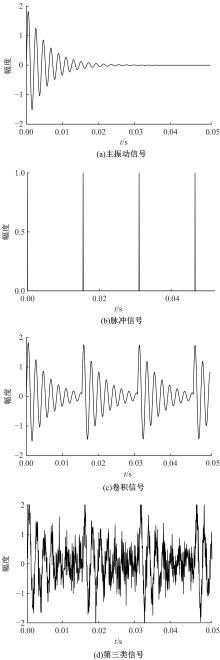
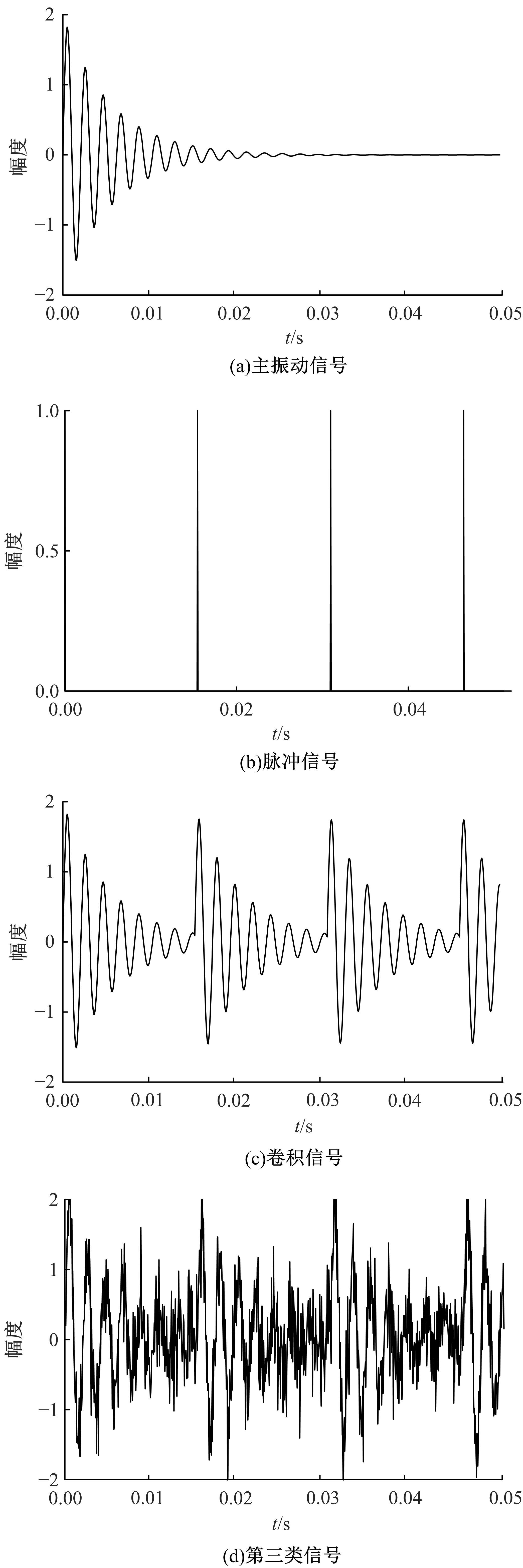
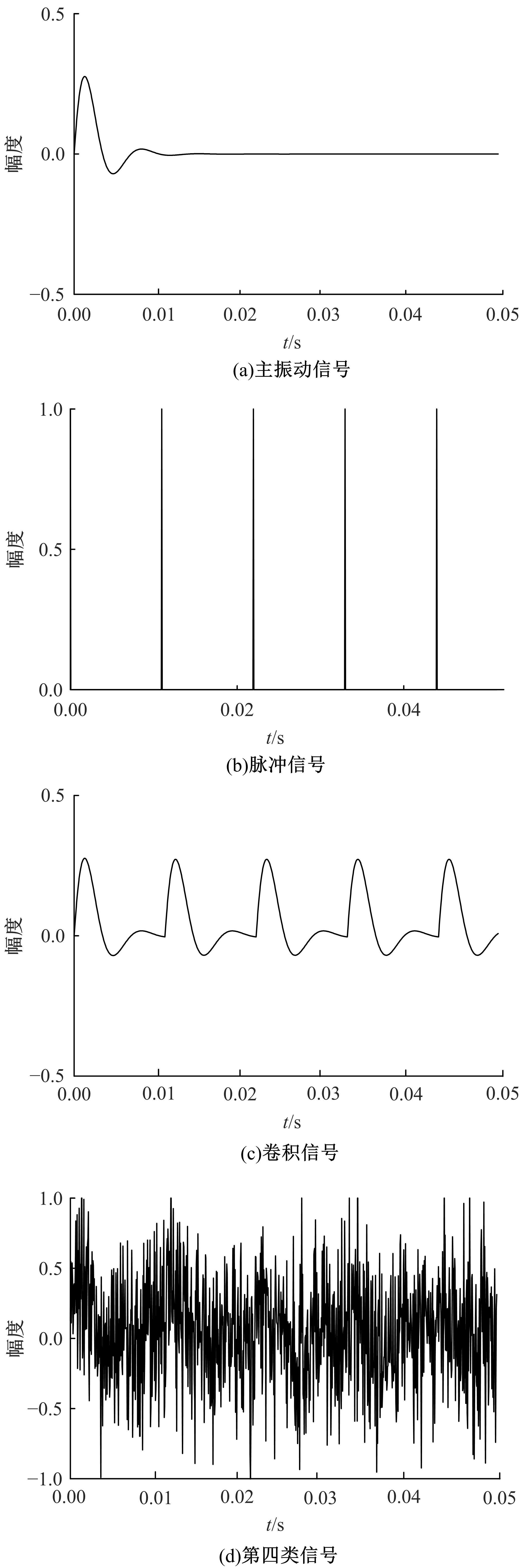
为了解决流形学习算法在欧式空间提取的特征不够显著的问题，提出了一种基于黎曼流形的稀疏图保持投影算法，并用于轴承的故障诊断。首先，计算原始数据的对称正定矩阵，构造对称正定流形（SPD流形）。其次，利用正则技术探索SPD流形中的稀疏结构，在此基础上分别建立样本的类内内在图和类间惩罚图，并通过图嵌入的方法实现数据的特征提取。实验结果表明，基于黎曼流形的稀疏图保持投影算法能提取到显著的特征。

关键词: 控制科学与工程, 黎曼流形, 稀疏表示, 图嵌入, 特征提取

Abstract:

To solve the problem that the feature extracted by the manifold learning algorithm in Euclidean space is not significant enough, this paper proposes a sparse graph preserving projection algorithm based on Riemannian manifold and applies it to bearing fault diagnosis. Firstly, the symmetric positive definite matrix of the original data is calculated to construct the Symmetric Positive Definite manifold (SPD manifold). Secondly, the sparse structure of the SPD manifold is explored by using the regularization technique. On this basis, the intrinsic graph of within-class and the penalty graph of the between-class of the sample are established respectively. Finally, the feature extraction of the data is realized by the method of graph embedding. Experimental results show that the sparse graph preserving projection algorithm based on Riemannian manifold can extract significant features.

Key words: control science and engineering, Riemannian manifold, sparse representation, graph embedding, feature extraction

中图分类号:

TP273

刘远红,郭攀攀,张彦生,李鑫. 基于黎曼流形的稀疏图保持投影的特征提取[J]. 吉林大学学报(工学版), 2021, 51(6): 2268-2279.

Yuan-hong LIU,Pan-pan GUO,Yan-sheng ZHANG,Xin LI. Feature extraction of sparse graph preserving projection based on Riemannian manifold[J]. Journal of Jilin University(Engineering and Technology Edition), 2021, 51(6): 2268-2279.

图/表 13

图1

图2

图3

图4

表1

不同算法在CWRU数据集上的Fisher度量"

算法	$t r (S b)$	$t r (S w)$	$F$
SPP	0.0913	1.3848	0.0659
LPP	3.18×10^-4	3.74×10^-5	8.5185
DSCPE	6.9762	0.2502	27.8793
黎曼SPP	4.73×10^-28	2.40×10^-27	0.1968
黎曼LPP	8.38×10^-28	2.97×10^-29	28.2356
SGPPRM	3.07×10^-29	5.38×10^-31	56.9958

表1

表2

不同算法在OL数据子集1上的Fisher度量"

算法	$t r (S b)$	$t r (S w)$	$F$
SPP	1.17×10^-6	1.42×10^-5	0.0820
LPP	3.10×10^-4	2.27×10^-5	13.7130
DSCPE	1.27×10^-4	7.63×10^-6	16.6818
黎曼SPP	1.16×10^-28	1.51×10^-26	0.0077
黎曼LPP	1.19×10^-30	2.18×10^-30	0.5450
SGPPRM	1.04×10^-21	7.98×10^-25	1300.0665

表2

表3

不同算法在OL数据子集2上的Fisher度量"

算法	$t r (S b)$	$t r (S w)$	$F$
SPP	3.02×10^-7	1.70×10^-5	0.0178
LPP	1.34×10^-4	8.54×10^-35	1.5740
DSCPE	1.73×10^-3	1.15×10^-4	15.0967
黎曼SPP	1.80×10^-30	5.18×10^-29	0.0347
黎曼LPP	1.99×10^-27	1.28×10^-28	15.5541
SGPPRM	2.62×10^-30	5.62×10^-32	46.6698

表3

图5

图6

图7

图8

图9

图10

参考文献 22

1	Dong S J, Sun D H, Tang B P, et al. A fault diagnosis method for rotating machinery based on PCA and morlet kernel SVM[J]. Mathematical Problems in Engineering, 2014, 2014(10): No. 293878.
2	Zhao X L,Ming P J. Fault diagnosis of rolling bearing based on feature reduction with global-local margin fisher analysis[J]. Neurocomputing, 2018, 315: 447-464.
3	Gao Z W, Cecati C, Ding S X. A survey of fault diagnosis and fault-tolerant techniques—part I: fault diagnosis with model-based and signal-based approaches[J]. IEEE Transactions on Industrial Electronics, 2015, 62(6): 3757-3767.
4	Belkin M, Niyogi P. Laplacian eigenmaps for dimensionality reduction and data representation[J]. Neural Computation, 2003, 15(6):1373-1396.
5	李勇, 陈贺新, 赵刚, 等. 基于可变k近邻LLE数据降维的图像检索方法[J]. 吉林大学学报:工学版, 2008, 38(4): 946-949.
	Li Yong, Chen He-xin, Zhao Gang, et al. Image retrieval method based on variable k nearest neighbor [J]. Journal of Jilin University (Engineering and Technology Edition), 2008, 38(4): 946-949.
6	孟广伟, 冯昕宇, 周立明,等. 基于降维算法的结构可靠性分析[J]. 吉林大学报:工学版, 2017, 47(1): 174-179.
	Meng Guang-wei, Feng Xin-yu, Zhou Li-ming, et al. Structural reliability analysis based on dimension reduction algorithm[J]. Journal of Jilin University (Engineering and Technology Edition),2017,47(1):174-179.
7	Qiao L S, Chen S C, Tan X Y. Sparsity preserving projections with applications to face recognition[J]. Pattern Recognition, 2010, 43(1):331-341.
8	殷俊, 杨万扣. 核稀疏保持投影及生物特征识别应用[J]. 电子学报, 2013, 41(4): 639-645.
	Yin Jun, Yang Wan-kou. Nuclear sparse preserving projection and application of biometric recognition[J]. Chinese Journal of Electronics, 2013, 41(4): 639-645.
9	Yan S C, Dong X, Zhang B Y, et al. Graph embedding and extensions: a general framework for dimensionality reduction[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2007, 29(1): 40-51.
10	Lou S J, Zhao X M, Chuang Y L, et al. Graph regularized sparsity discriminant analysis for face recognition[J]. Sensors and Actuators, 2016, 173: 290-297.
11	Zhang L M, Chen S C, Qiao L S. Graph optimization for dimensionality reduction with sparsity constraints[J]. Pattern Recognition, 2012, 45(3):1205-1210.
12	Yang W K, Wang Z Y, Sun C Y. A collaborative representation based projections method for feature extraction[J]. Pattern Recognition, 2015, 48(1): 20-27.
13	Ma Y, Wu X H. Discriminant sparse and collaborative preserving embedding for bearing fault diagnosis[J]. Neurocomputing, 2018, 313: 259-270.
14	蔡金金, 刘博, 马跃进, 等. 多黎曼流形的判别分析与融合[J]. 河北农业大学学报, 2019, 42(1): 114-121.
	Cai Jin-jin, Liu Bo, Ma Yue-jin, et al. Discriminant analysis and fusion of multi Riemannian manifolds [J].
	Journal of Agricultural University of Hebei, 2019, 42(1): 114-121.
15	Harandi M, Salzmann M, Hartley R. Dimensionality reduction on spd manifolds: the emergence of geometry-aware methods[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2017, 40(1):48-62.
16	Xie X F, Zhu L Y, Gu Z H, et al. Classification of symmetric positive definite matrices based on bilinear isometric Riemannian embedding[J]. Pattern Recognition, 2019, 87: 94-105.
17	Cheng J, Ghosh A, Jiang T Z, et al. A Riemannian framework for orientation distribution function computing[J/OL]. [2020-06-03].
18	Arsigny V, Fillard P, Pennec X, et al. Log-Euclidean metrics for fast and simple calculus on diffusion tensors[J]. Magnetic Resonance in Medicine, 2010, 56(2): 411-421.
19	Cherian A, Sra S, Banerjee A, et al. Jensen-bregman logdet divergence with application to efficient similarity search for covariance matrices[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2013, 35(9): 2161-2174.
20	Arsigny V, Fillard P, Pennec X, et al. Geometric means in a novel vector space structure on symmetric positive-definite matrices[J]. Siam Journal on Matrix Analysis & Applications, 2011, 29(1): 328-347.
21	Lovri´c M, Min-Oo M, Ruh E A. Multivariate normal distributions parametrized as a Riemannian symmetric space[J]. Journal of Multivariate Analysis, 2000, 74(1): 36-48.
22	He X F, Yan S C, Hu Y X, et al. Face recognition using laplacianfaces[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2005, 27(3): 328-340.

相关文章 15

[1]	钟辉,康恒,吕颖达,李振建,李红,欧阳若川. 基于注意力卷积神经网络的图像篡改定位算法[J]. 吉林大学学报(工学版), 2021, 51(5): 1838-1844.
[2]	朱小龙,谢忠. 基于海量文本数据的知识图谱自动构建算法[J]. 吉林大学学报(工学版), 2021, 51(4): 1358-1363.
[3]	陈广秋,陈昱存,李佳悦,刘广文. 基于DNST和卷积稀疏表示的红外与可见光图像融合[J]. 吉林大学学报(工学版), 2021, 51(3): 996-1010.
[4]	徐涛,马克,刘才华. 基于深度学习的行人多目标跟踪方法[J]. 吉林大学学报(工学版), 2021, 51(1): 27-38.
[5]	何德峰,罗捷,舒晓翔. 自主网联车辆时滞反馈预测巡航控制[J]. 吉林大学学报(工学版), 2021, 51(1): 349-357.
[6]	王洪雁,邱贺磊,郑佳,裴炳南. 光照变化下基于低秩稀疏表示的视觉跟踪方法[J]. 吉林大学学报(工学版), 2020, 50(1): 268-277.
[7]	耿庆田, 于繁华, 王宇婷, 高琦坤. 基于特征融合的车型检测新算法[J]. 吉林大学学报(工学版), 2018, 48(3): 929-935.
[8]	董强, 刘晶红, 周前飞. 用于遥感图像拼接的改进SURF算法[J]. 吉林大学学报(工学版), 2017, 47(5): 1644-1652.
[9]	尹明, 战荫伟, 裴海龙. 基于稀疏补算子学习的图像融合方法[J]. 吉林大学学报(工学版), 2016, 46(6): 2052-2058.
[10]	肖钟捷. 基于小波空间特征谱熵的数字图像识别[J]. 吉林大学学报(工学版), 2015, 45(6): 1994-1998.
[11]	刘红，孙爽滋，王庆元，李延忠. 基于PSO的模拟电路故障信息特征提取[J]. 吉林大学学报(工学版), 2015, 45(2): 675-680.
[12]	潘海阳, 刘顺安, 姚永明. 基于深度信息的自主空中加油技术[J]. 吉林大学学报(工学版), 2014, 44(6): 1750-1756.
[13]	李学军, 杨晟, 李振举, 杨阿华, 刘涛. 与高精度单点匹配式定位算法[J]. 吉林大学学报(工学版), 2014, 44(4): 1197-1202.
[14]	查长军,韦穗,杨海蓉,丁大为. 基于稀疏表示的多类融合样本中特定目标识别[J]. 吉林大学学报(工学版), 2014, 44(3): 822-827.
[15]	顾播宇,孙俊喜,李洪祚,刘红喜,刘广文. 基于特征加权模块双方向二维主成分分析的人脸识别[J]. 吉林大学学报(工学版), 2014, 44(3): 828-833.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed