基于快速非奇异终端滑模的机械臂轨迹跟踪方法

doi:10.13229/j.cnki.jdxbgxb20181083

吉林大学学报(工学版) ›› 2020, Vol. 50 ›› Issue (2): 464-471.doi: 10.13229/j.cnki.jdxbgxb20181083

• 车辆工程·机械工程 • 上一篇

基于快速非奇异终端滑模的机械臂轨迹跟踪方法

王伟^1,²(),赵健廷^1,²,胡宽荣³,郭永仓⁴

^1.北京理工大学宇航学院, 北京 100081
^2.北京理工大学无人机自主控制技术北京市重点实验室, 北京 100081
^3.西北工业集团科研设计所, 西安 710299
^4.西北工业集团质量部, 西安 710299

收稿日期:2018-10-27 出版日期:2020-03-01 发布日期:2020-03-08
作者简介:王伟（1984-），男，讲师，博士.研究方向：飞行器总体设计，控制工程.E-mail:wangweiyh@bit.edu.cn
基金资助:
国家自然科学基金项目(61172182)

Trajectory tracking of robotic manipulators based on fast nonsingular terminal sliding mode

Wei WANG^1,²(),Jian-ting ZHAO^1,²,Kuan-rong HU³,Yong-cang GUO⁴

^1.School of Aerospace Engineering，Beijing Institute of Technology，Beijing 100081，China
^2.Beijing Key Laboratory of UAV Autonomous Control Technology，Beijing Institute of Technology，Beijing 100081，China
^3.Research and Design Institute，Northwest Industrial Group，Xi'an 710299，China
^4.Quality Department，Northwest Industrial Group，Xi'an 710299，China

Received:2018-10-27 Online:2020-03-01 Published:2020-03-08

摘要/Abstract

摘要：

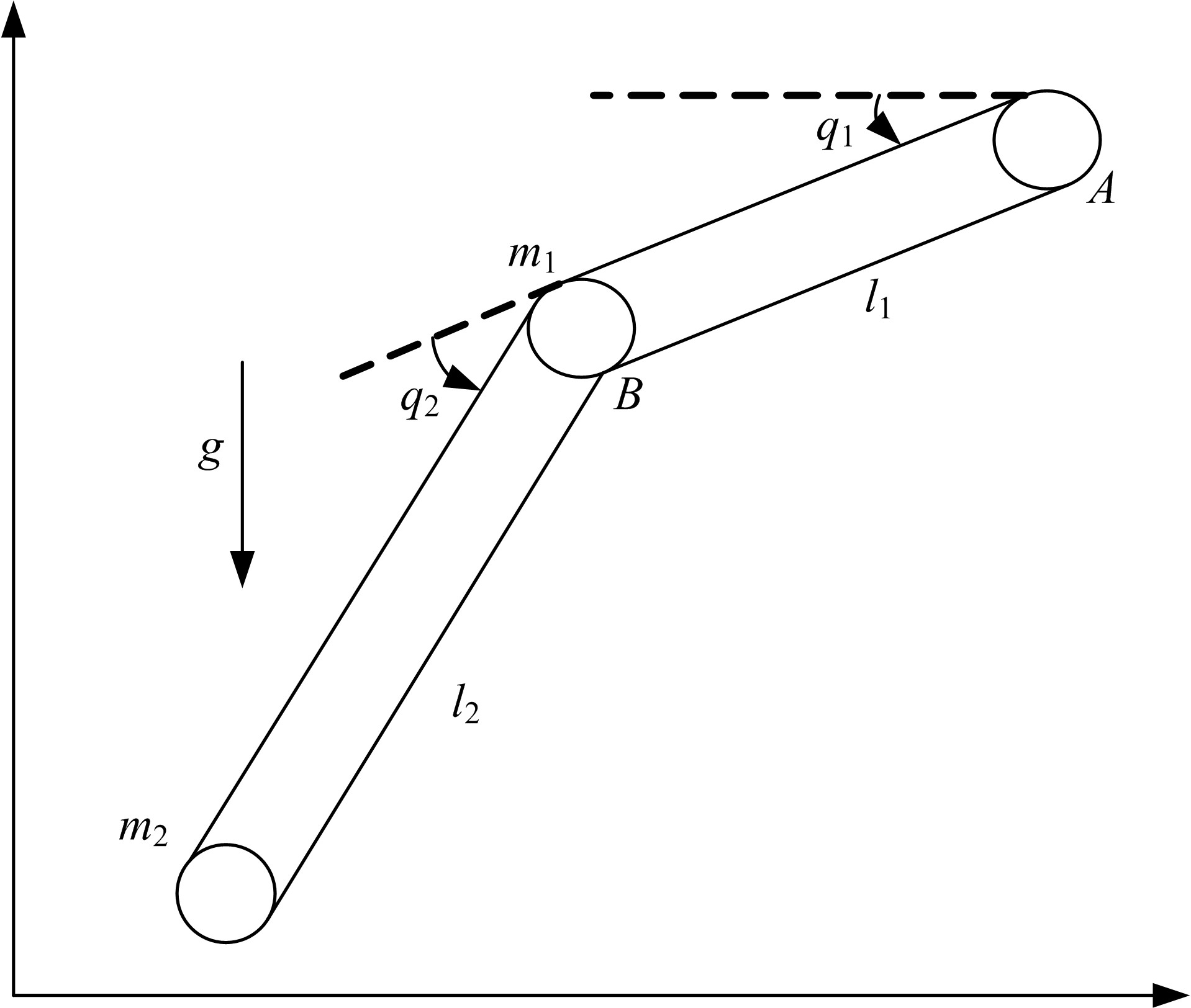
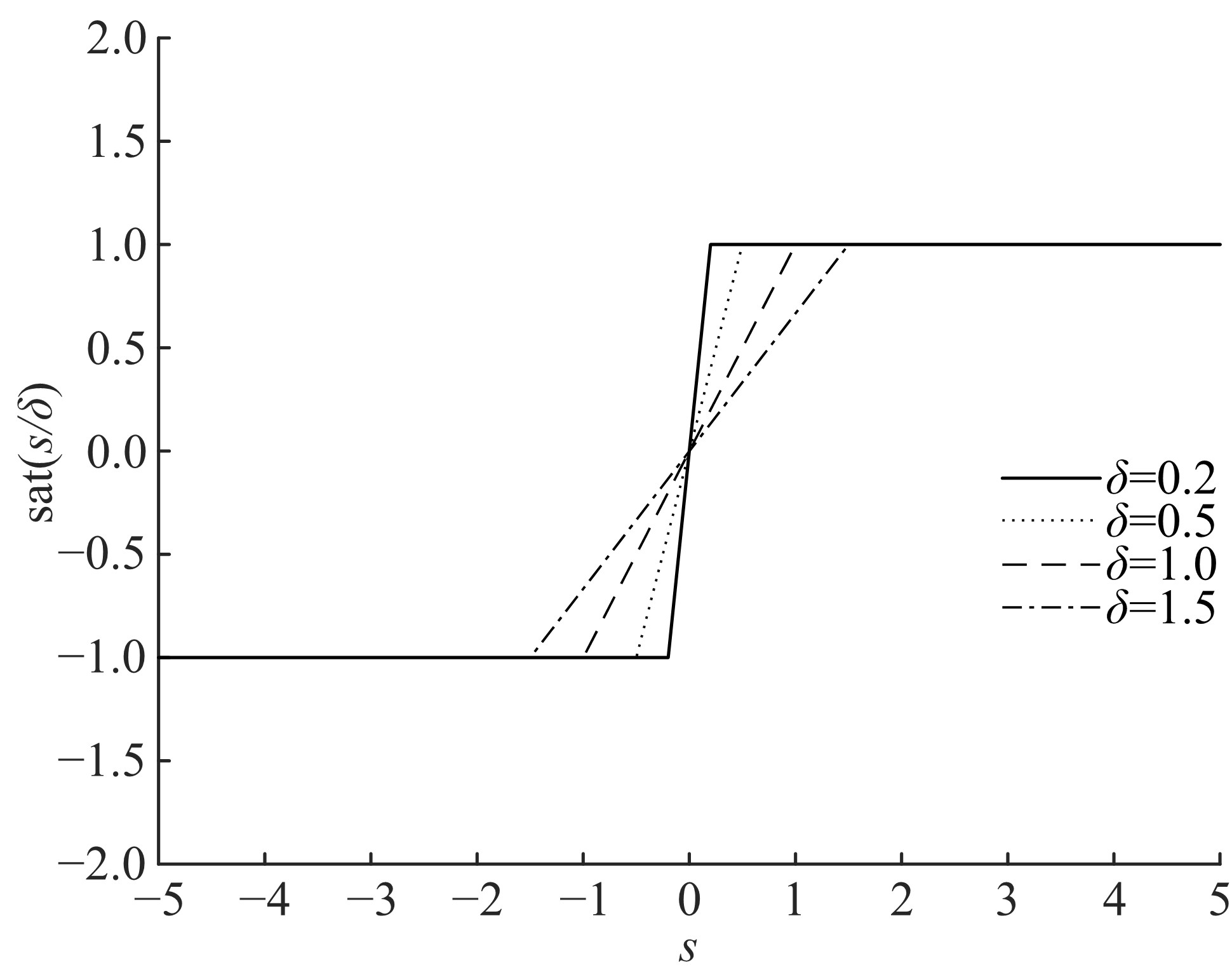
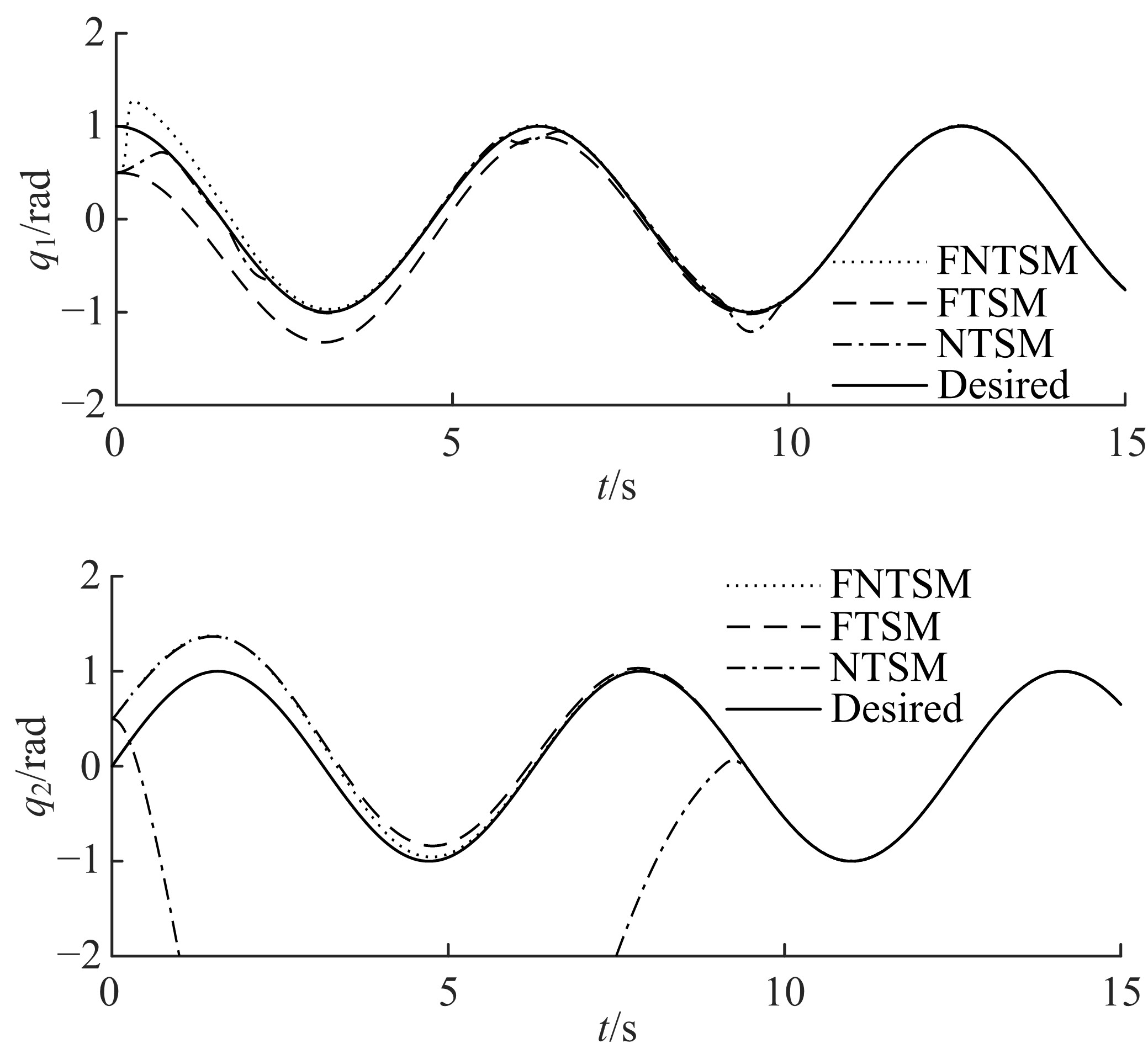
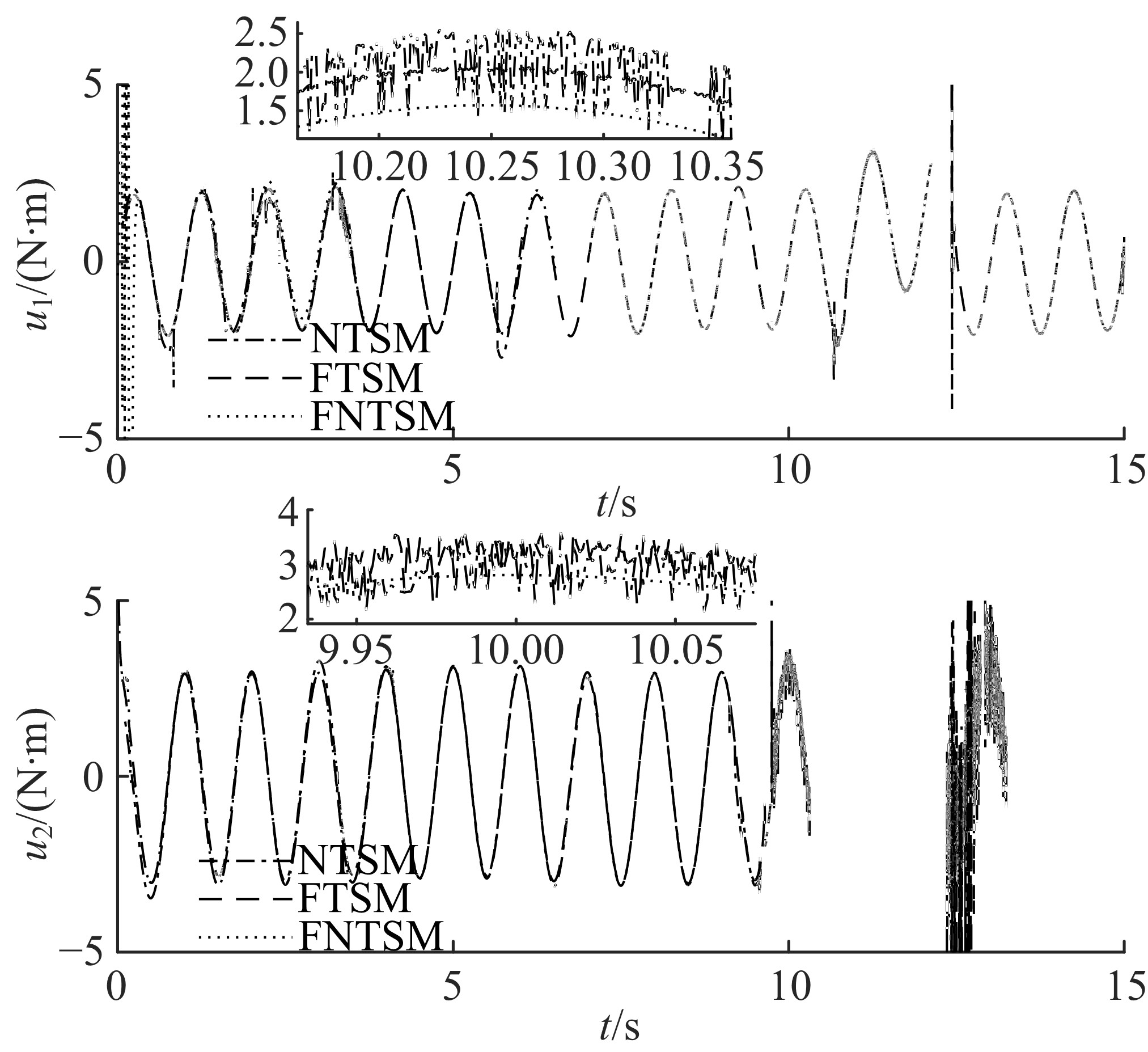
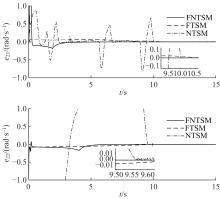
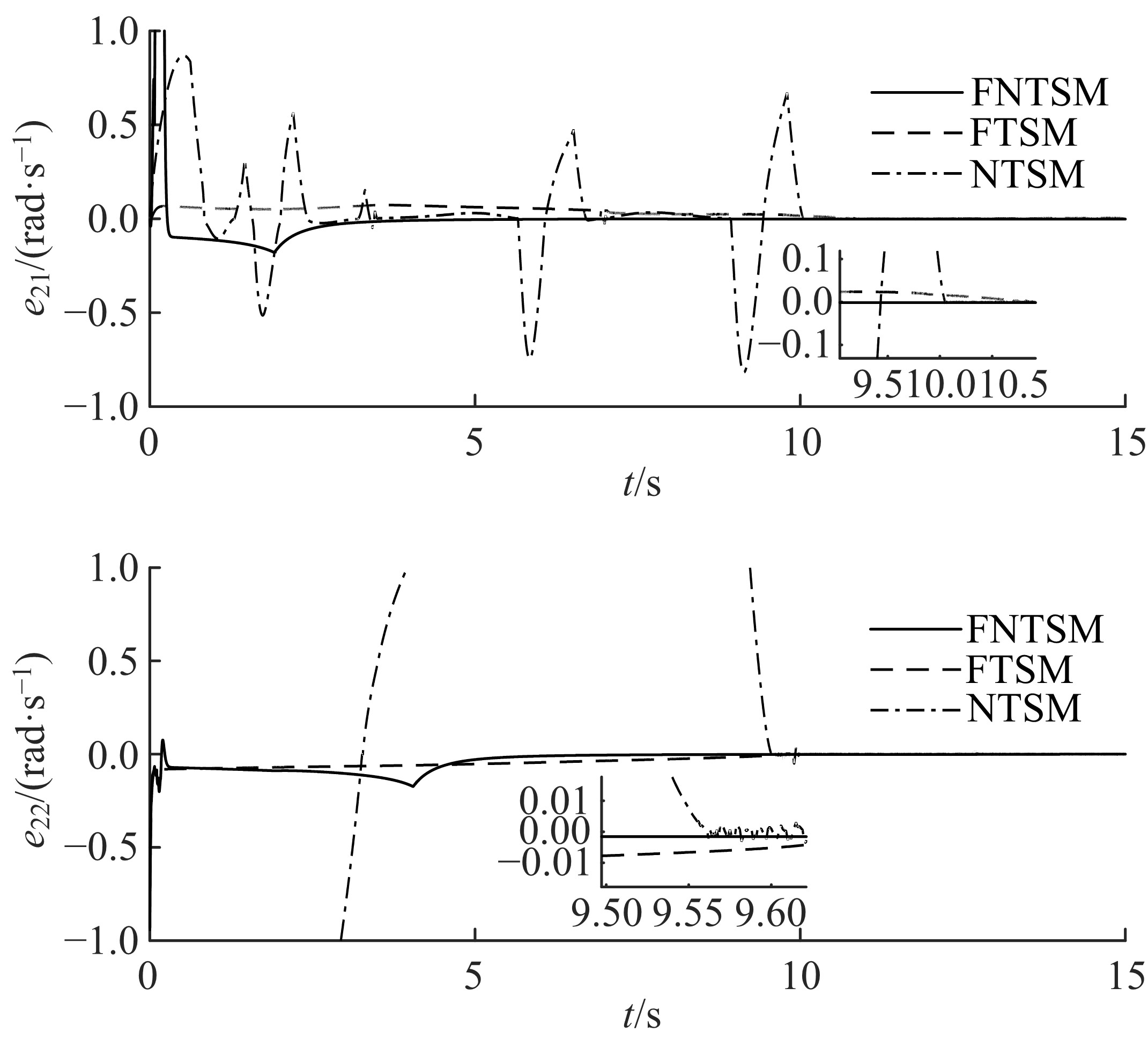
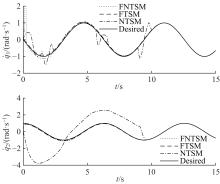
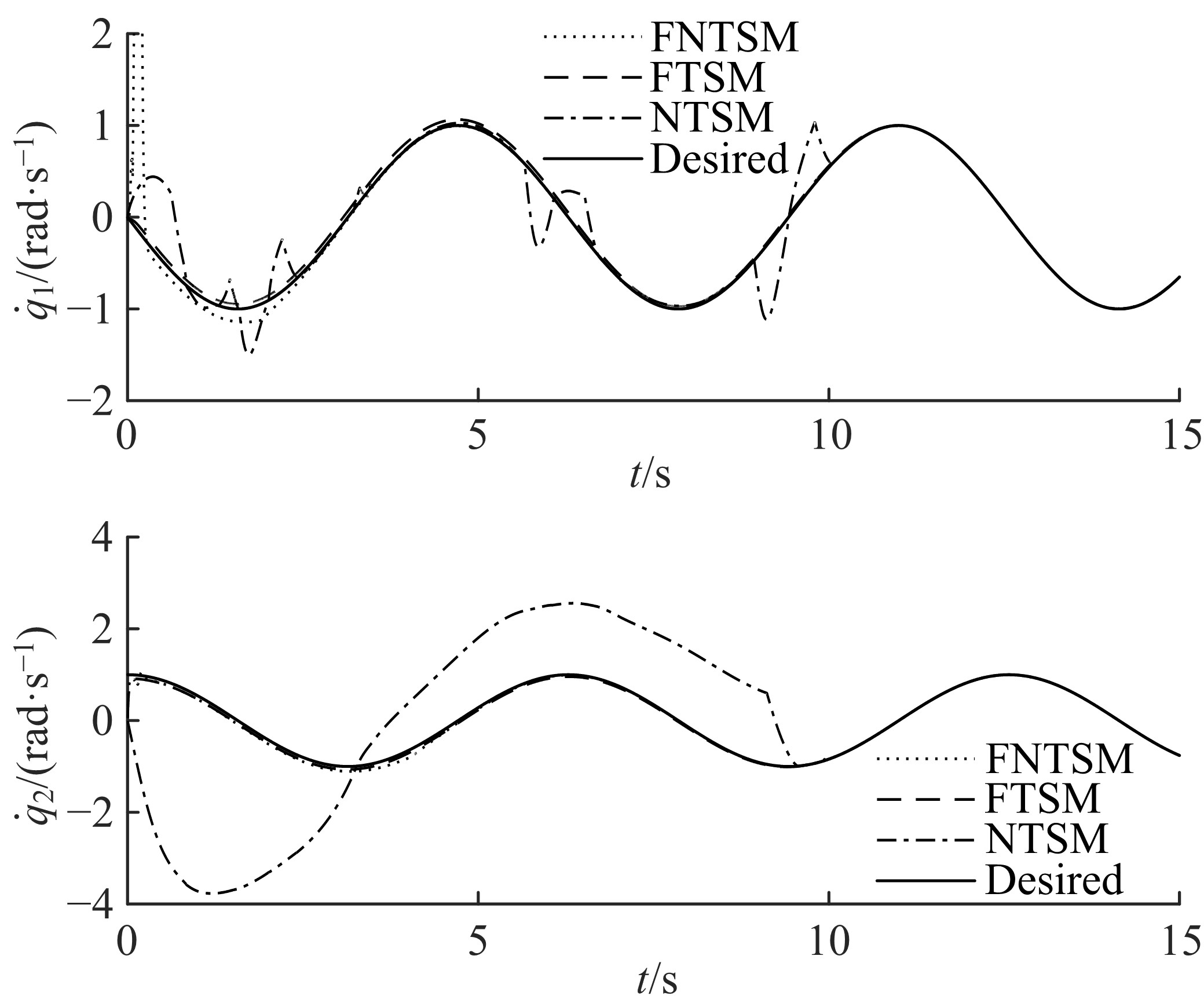
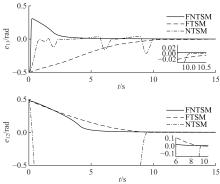
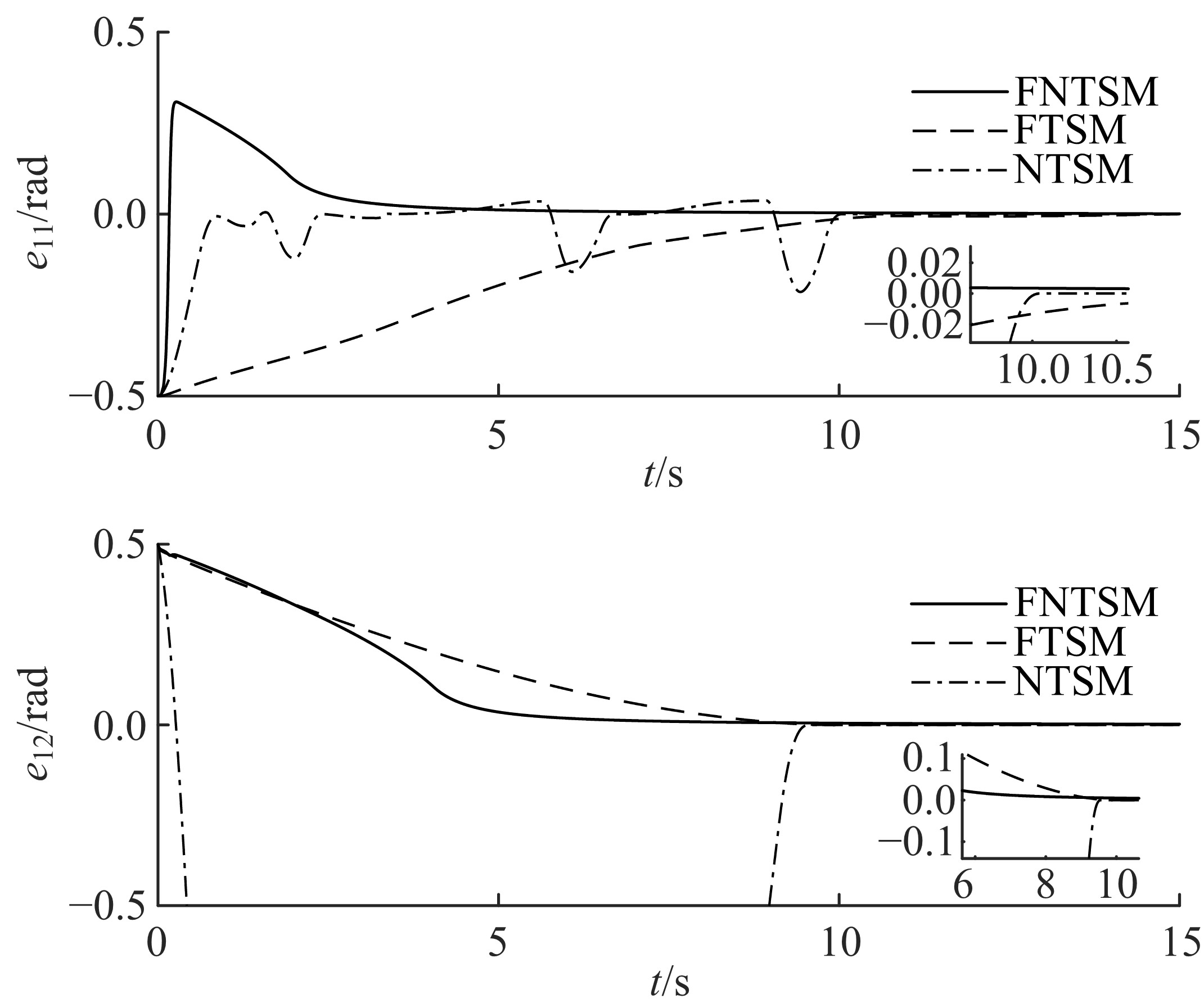
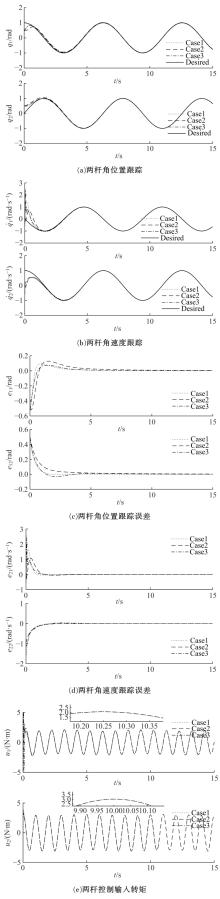
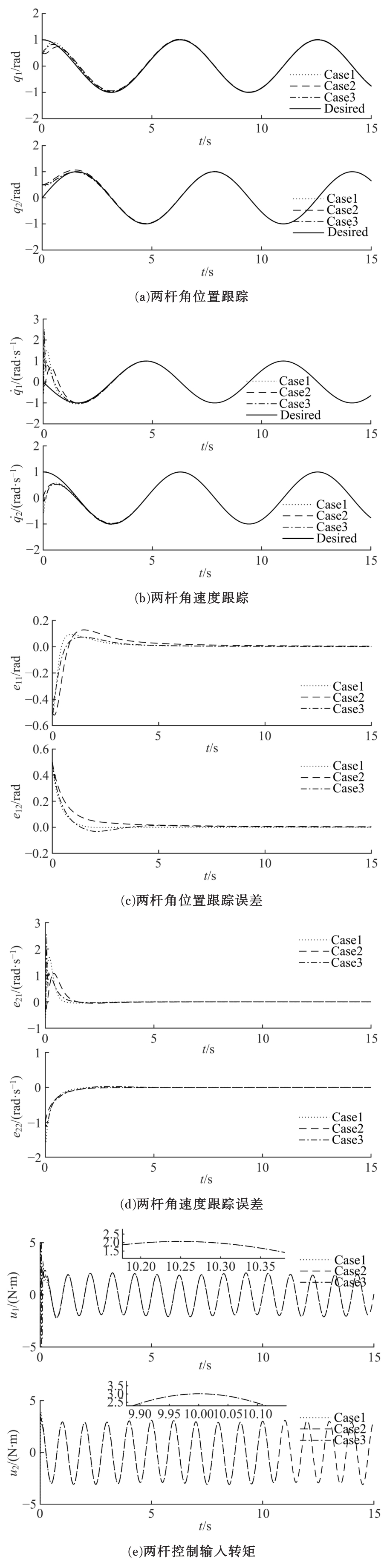
为使机械臂按预定轨迹运行，设计了一种基于快速非奇异终端滑模的新型现代控制方法。该方法结合了传统的快速终端滑模和非奇异终端滑模，具有快速性、非奇异性、有限时间收敛性和强鲁棒性，并可有效抑制滑模控制器固有的抖振现象。首先，将机械臂简化为二自由度刚性连杆系统并建立数学模型；其次，设计鲁棒控制器；然后，构造李雅普诺夫函数验证其稳定性；最后，详细的对比仿真表明了本文方法的有效性。

关键词: 自动控制技术, 机械臂控制, 终端滑模控制理论, 非奇异性, 有限时间收敛性

Abstract:

To drive the robotic manipulator tracking the desired trajectory, a novel modern control method based on the nonsingular terminal sliding mode is designed in this paper. Combining the traditional fast terminal sliding mode and the nonsingular terminal sliding mode, the proposed control method possesses the characteristics of rapidity, nonsingularity, finite-time convergence and strong robustness. The chattering from sliding mode controller can also be suppressed effectively. Here, the mathematical model of robotic manipulator structure which can be simplified as a 2-DOF rigid linkage system is built, firstly. Next, a robust controller is designed. Then, the Lyapunov function is constructed to verify its stability. Finally, detailed simulations with some comparisons demonstrate the effectiveness of the proposed method.

Key words: automatic control technology, manipulator control, terminal sliding mode control theory, nonsingularity, finite-time convergence

中图分类号:

TP273

王伟,赵健廷,胡宽荣,郭永仓. 基于快速非奇异终端滑模的机械臂轨迹跟踪方法[J]. 吉林大学学报(工学版), 2020, 50(2): 464-471.

Wei WANG,Jian-ting ZHAO,Kuan-rong HU,Yong-cang GUO. Trajectory tracking of robotic manipulators based on fast nonsingular terminal sliding mode[J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(2): 464-471.

图/表 10

图1

图2

表1

各滑模及控制器设计参数"

滑模及控制器	$β$	$a$	$b$	$ε$
FTSM	$7.5$	$5$	$3$	$5$
NTSM	$7.5$	$5$	$3$	$5$
FNTSM	$7.5$	$5$	$3$	$5$

表1

图3

图7

图6

图4

图5

表2

控制参数"

Case	$β$	$λ$	$α$
1	7.50	150	100
2	3.75	150	100
3	7.50	75	50

表2

图8

参考文献 20

1	Kreutz K. On manipulator control by exact linearization[J]. IEEE Transactions on Automatic Control, 1989, 34(7): 763-767.
2	He W, Dong Y, Sun C. Adaptive neural impedance control of a robotic manipulator with input saturation[J]. IEEE Transactions on Systems Man & Cybernetics Systems, 2016, 46(3): 334-344.
3	Poignet P. and Gautier M. Nonlinear model predictive control of a robot manipulator[C]∥Proceedings of the 6th International Workshop on Advanced Motion Control Proceedings, Nagoya, Japan, 2000: 401-406.
4	李英, 朱明超, 李元春. 可重构机械臂模糊神经补偿控制[J]. 吉林大学学报: 工学版, 2007, 37(1): 206-211.
	Li Ying, Zhu Ming-chao, Li Yuan-chun. Neurofuzzy compensation control for reconfigurable manipulator[J]. Journal of Jilin University (Engineering and Technology Edition), 2007, 37(1): 206-211.
5	Abdulridha H M, Hassoun Z A. Control design of robotic manipulator based on quantum neural network[J]. Journal of Dynamic Systems Measurement and control, 2018, 140(6): 61-71.
6	Liu M. Decentralized control of robot manipulators: nonlinear and adaptive approaches[J]. Automatic Control IEEE Transactions on, 1999, 44(2): 357-363.
7	张友安, 糜玉林, 吕凤琳, 等. 双连杆柔性臂自适应模糊滑模控制[J]. 吉林大学学报: 工学版, 2005, 35(5): 520-525.
	Zhang You-an, Mi Yu-lin, Feng-lin Lyv, et al. Adaptive fuzzy sliding mode control for two-link flexible manipulator[J]. Journal of Jilin University (Engineering and Technology Edition), 2005, 35(5): 520-525.
8	Feng Y, Yu X, Man Z. Non-singular terminal sliding mode control of rigid manipulators[J]. Automatica, 2002, 38(12): 2159-2167.
9	Youcef-Toumi K, Asada H. The design and control of manipulators with decoupled and configuration-invariant inertia tensors[C]∥American Control Conference, Seattle, WA, USA, 1986: 811-817.
10	Su Y, Dong S, Lu R, et al. Integration of saturated PI synchronous control and PD feedback for control of parallel manipulators[J]. IEEE Transactions on Robotics, 2006, 22(1): 202-207.
11	Tomizuka M, Horowitz R. Model reference adaptive control of mechanical manipulators[J]. IFAC Proceedings Volumes, 1983, 16(9): 27-32.
12	He W, Chen Y, Yin Z. Adaptive neural network control of an uncertain robot with full-state constraints[J]. IEEE Transactions on Cybernetics, 2017, 46(3): 620-629.
13	Sun C, He W, Hong J. Neural network control of a flexible robotic manipulator using the lumped spring-mass model[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2017, 47(8): 1863-1874.
14	Yu X, Man Z. Fast terminal sliding-mode control design for nonlinear dynamical systems[J]. IEEE Transactions on Circuits & Systems I Fundamental Theory & Applications, 2002, 49(2): 261-264.
15	Feng Y, Yu X, Man Z. Non-singular terminal sliding mode control of rigid manipulators[J]. Automatica, 2002, 38(12): 2159-2167.
16	Chen S Y, Lin F J. Robust nonsingular terminal sliding-mode control for nonlinear magnetic bearing system[J]. IEEE Transactions on Control Systems Technology, 2011, 19(3): 636-643.
17	Shtessel Y, Taleb M, Plestan F. A novel adaptive-gain supertwisting sliding mode controller: methodology and application[J]. Automatica, 2012, 48(5):759-769.
18	Zhang M, Tian P, Chen X, et al. Ground target tracking guidance law for fixed-wing unmanned aerial vehicle: a search and capture approach[J]. Journal of Dynamic Systems Measurement and Control, 2017， 139(10): 45-50.
19	He S, Lin D, Wang J. Chattering-free adaptive fast convergent terminal sliding mode controllers for position tracking of robotic manipulators[J]. Proceedings of The Institution of Mechanical Engineers Part C: Journal of Mechanical Engineering Science, 2015, 230(4): 514-526.
20	Moreno J A, Osorio M. Strict lyapunov functions for the super-twisting algorithm[J]. IEEE Transactions on Automatic Control, 2012, 57(4): 1035-1040.

相关文章 15

[1]	刘富,安毅,董博,李元春. 基于ADP的可重构机械臂能耗保代价分散最优控制[J]. 吉林大学学报(工学版), 2020, 50(1): 342-350.
[2]	曲兴田,王学旭,孙慧超,张昆,闫龙威,王宏一. 熔融沉积成型技术3D打印机加热系统的模糊自适应PID控制[J]. 吉林大学学报(工学版), 2020, 50(1): 77-83.
[3]	马常友, 高海波, 丁亮, 于海涛, 邢宏军, 邓宗全. 机器人末端执行器自更换机构设计及对接策略[J]. 吉林大学学报(工学版), 2019, 49(6): 2027-2037.
[4]	马苗苗,潘军军,刘向杰. 含电动汽车的微电网模型预测负荷频率控制[J]. 吉林大学学报(工学版), 2019, 49(5): 1644-1652.
[5]	于树友,谭雷,王伍洋,陈虹. 基于三步法的汽车主动四轮转向控制[J]. 吉林大学学报(工学版), 2019, 49(3): 934-942.
[6]	温海营,任翔,徐卫良,丛明,秦文龙,胡书海. 咀嚼机器人颞下颌关节仿生设计及试验测试[J]. 吉林大学学报(工学版), 2019, 49(3): 943-952.
[7]	顾万里,王萍,胡云峰,蔡硕,陈虹. 具有H_∞性能的轮式移动机器人非线性控制器设计[J]. 吉林大学学报(工学版), 2018, 48(6): 1811-1819.
[8]	李战东,陶建国,罗阳,孙浩,丁亮,邓宗全. 核电水池推力附着机器人系统设计[J]. 吉林大学学报(工学版), 2018, 48(6): 1820-1826.
[9]	赵爽,沈继红,张刘,赵晗,陈柯帆. 微细电火花加工表面粗糙度快速高斯评定[J]. 吉林大学学报(工学版), 2018, 48(6): 1838-1843.
[10]	王德军, 魏薇郦, 鲍亚新. 考虑侧风干扰的电子稳定控制系统执行器故障诊断[J]. 吉林大学学报(工学版), 2018, 48(5): 1548-1555.
[11]	闫冬梅, 钟辉, 任丽莉, 王若琳, 李红梅. 具有区间时变时滞的线性系统稳定性分析[J]. 吉林大学学报(工学版), 2018, 48(5): 1556-1562.
[12]	张茹斌, 占礼葵, 彭伟, 孙少明, 刘骏富, 任雷. 心肺功能评估训练系统的恒功率控制[J]. 吉林大学学报(工学版), 2018, 48(4): 1184-1190.
[13]	董惠娟, 于震, 樊继壮. 基于激光测振仪的非轴对称超声驻波声场的识别[J]. 吉林大学学报(工学版), 2018, 48(4): 1191-1198.
[14]	张士涛, 张葆, 李贤涛, 王正玺, 田大鹏. 基于零相差轨迹控制方法提升快速反射镜性能[J]. 吉林大学学报(工学版), 2018, 48(3): 853-858.
[15]	田彦涛, 张宇, 王晓玉, 陈华. 基于平方根无迹卡尔曼滤波算法的电动汽车质心侧偏角估计[J]. 吉林大学学报(工学版), 2018, 48(3): 845-852.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

基于快速非奇异终端滑模的机械臂轨迹跟踪方法

Trajectory tracking of robotic manipulators based on fast nonsingular terminal sliding mode

RICH HTML

PDF (PC)

摘要/Abstract

引用本文

使用本文

图/表 10

参考文献 20

相关文章 15

Metrics

本文评价

推荐阅读 0