吉林大学学报(工学版) ›› 2022, Vol. 52 ›› Issue (3): 525-532.doi: 10.13229/j.cnki.jdxbgxb20200849
• 车辆工程·机械工程 • 上一篇
基于粒子群优化模糊C焊缝等级磁记忆定量识别模型
- 东北石油大学 机械科学与工程学院,黑龙江 大庆 163318
Quantitative metal magnetic memory classification model of weld grades based on particle swarm optimization fuzzy C⁃means
Hai-yan XING( ),Chao LIU,Cheng XU,Yu-huan CHEN,Song-hong-ze WANG
),Chao LIU,Cheng XU,Yu-huan CHEN,Song-hong-ze WANG
- School of Mechanical Science and Engineering,Northeast Petroleum University,Daqing 163318,China
摘要:
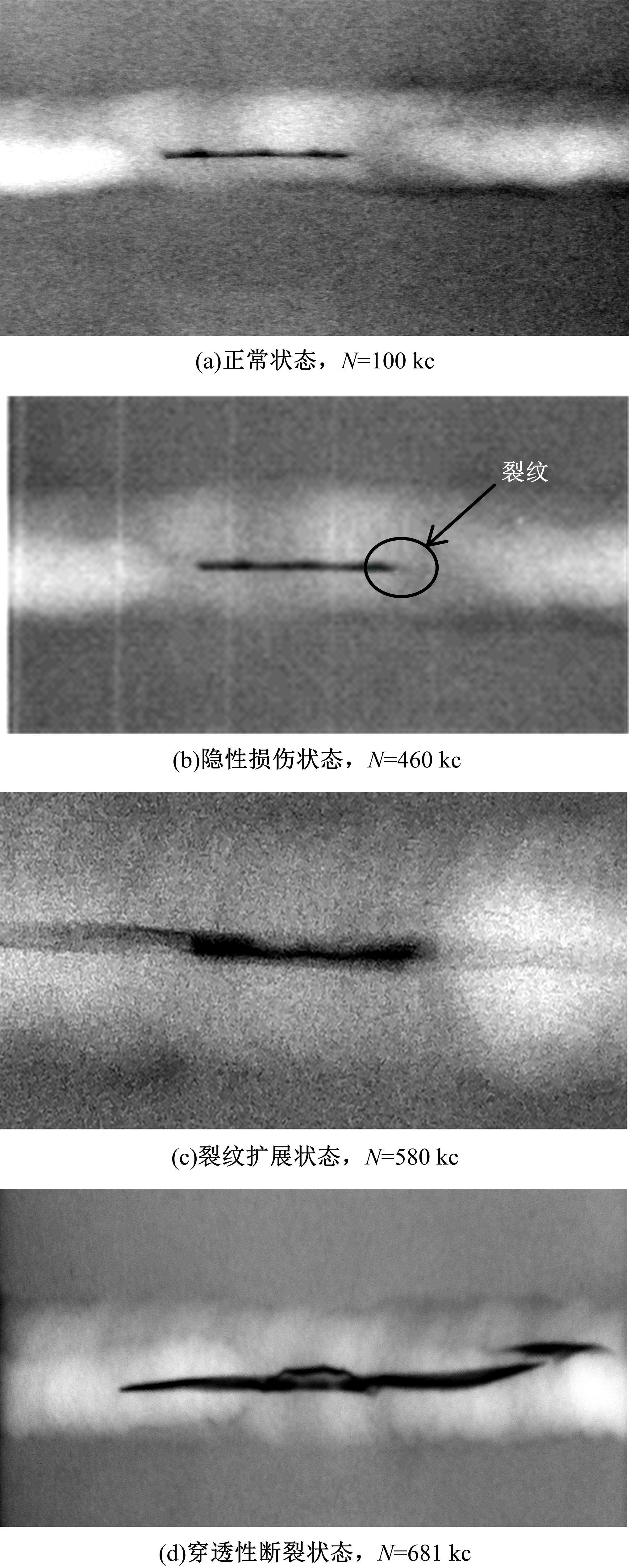
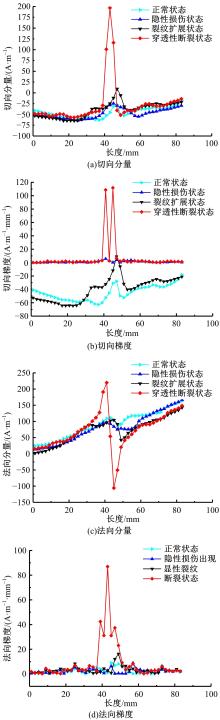
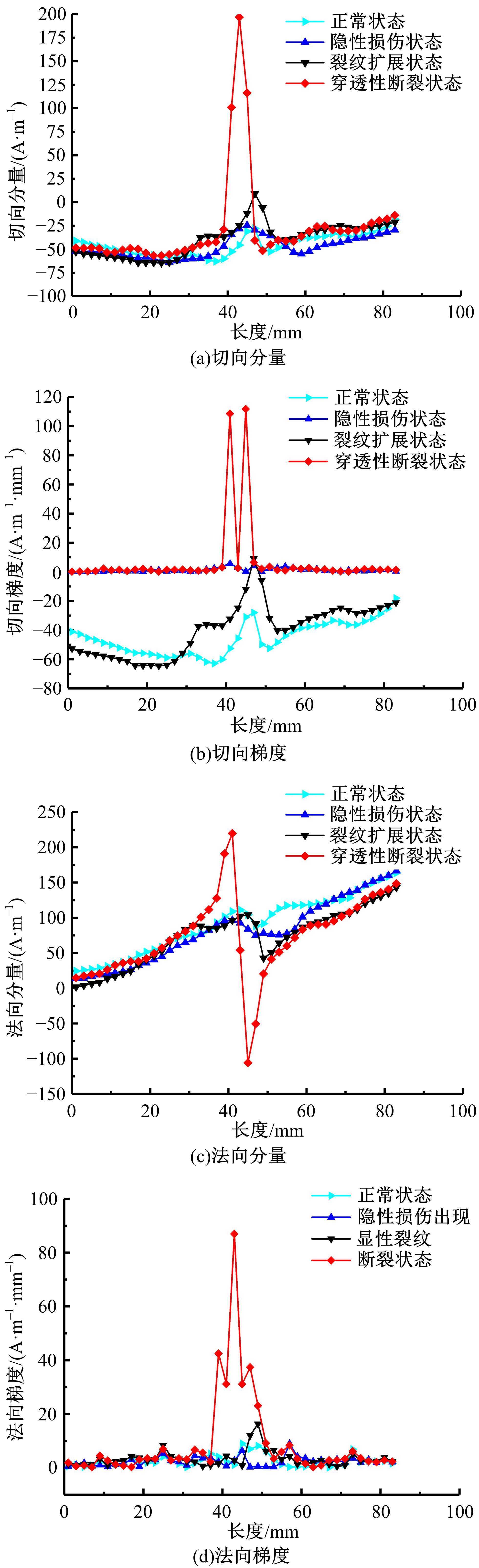
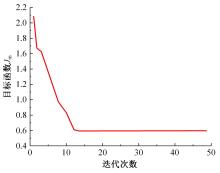
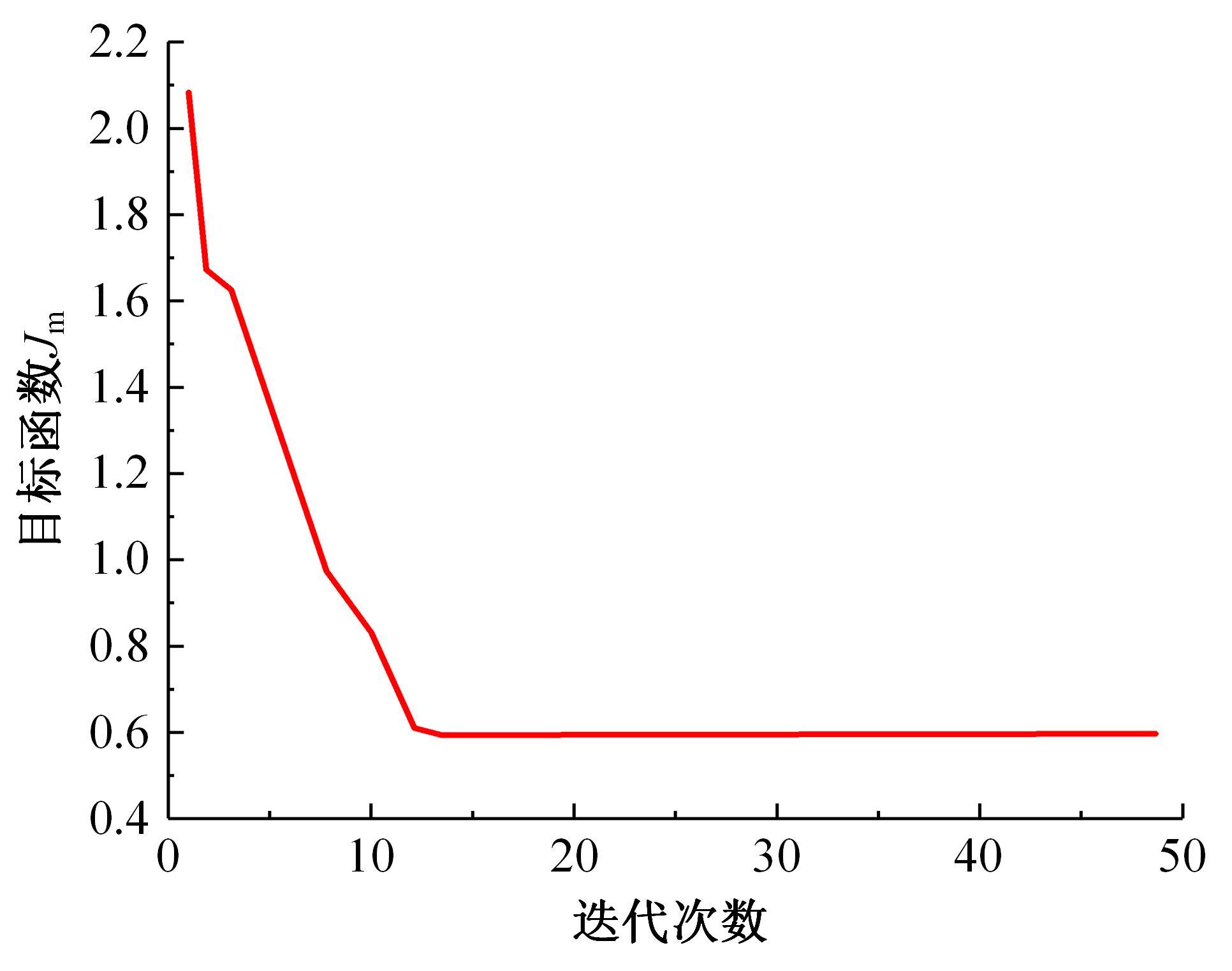
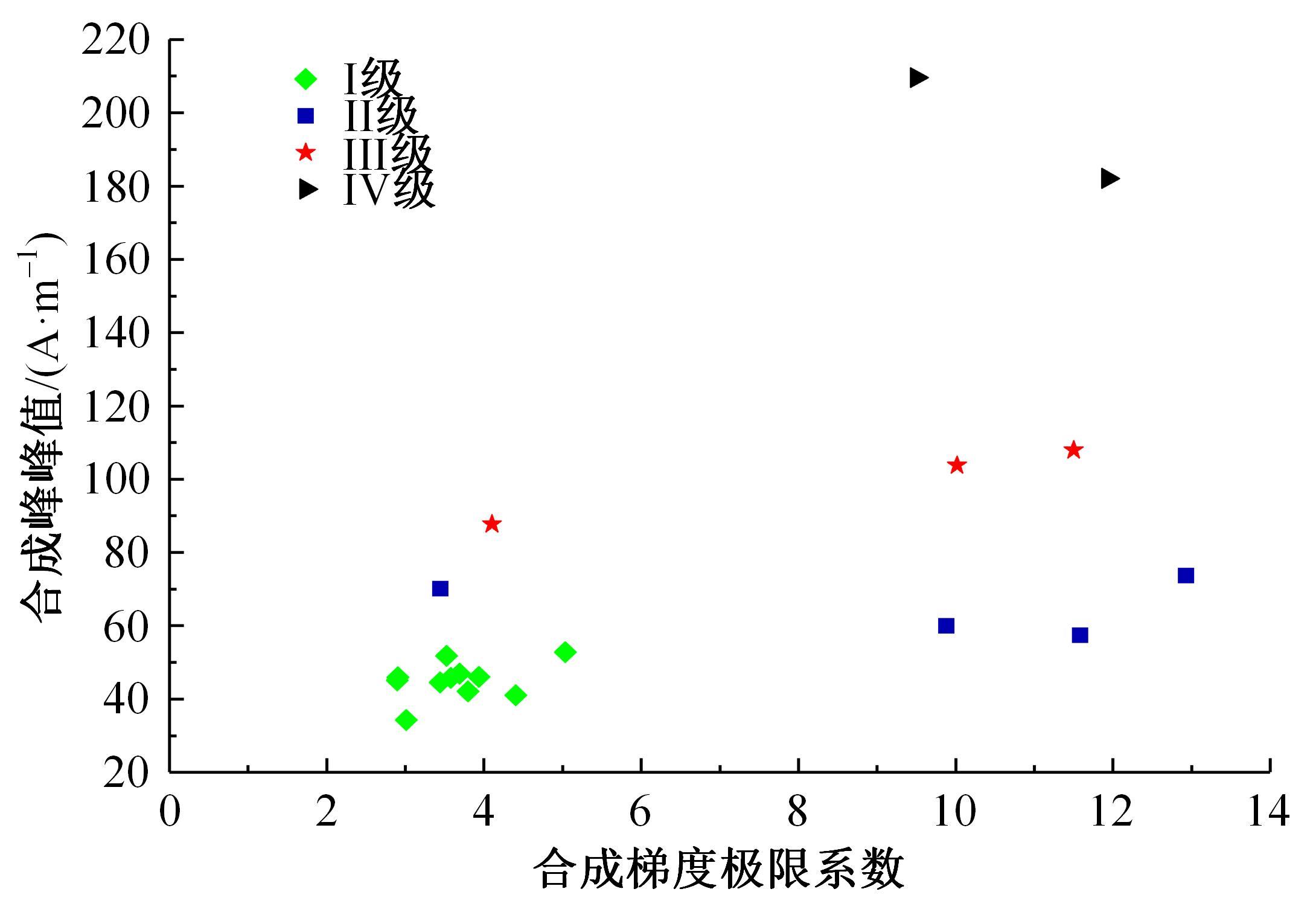
针对不同焊缝等级之间磁记忆特征参数的模糊性导致的定量等级识别困题的问题,提出了基于粒子群优化模糊C均值聚类算法(FCM)的焊缝等级定量识别模型。以Q235钢预制未焊透焊缝试件为试验材料,进行疲劳拉伸试验,采用TSC-5M-32型金属磁记忆检测仪进行磁记忆信号检测,提取三维合成特征参数向量作为实验数据,同时将磁记忆检测结果与X射线检测结果进行对比以提供对照依据。考虑到FCM初始聚类中心随机确定,易陷入局部最优,同时人为设置权值m易导致聚类精度不高,引入具有全局搜索和高效运算能力的粒子群算法,对FCM的初始聚类中心及权值m进行优化。将FCM目标函数倒数的修正公式作为粒子群算法的适应函数,样本个体及权值m作为粒子进行编码,通过更新粒子速度和位置,获得全局最优聚类中心并将m收敛到最优解,建立了基于粒子群优化FCM的焊缝等级定量识别模型。模型验证结果表明,模型分类正确率达97.93%,可为实际工程焊缝临界状态识别和设备安全定量评价提供新思路。
中图分类号:
- TH13
| 1 | , 焊缝无损检测·超声检测技术、检测等级和评定 [S]. |
| 2 | Dubov A A. Study of metal properties using metal magnetic memory method[C]∥7th European Conference on Non-destructive Testing, Copenhagen,1997:920-927. |
| 3 | Doubov A A. Diagnostics of metal items and equipment by means of metal magnetic memory [C]∥Proceedings of the CHSNDT 7th Conference on NDT and International Research Symposium, Shantou, China, 1999: 287-293. |
| 4 | Dubov A A. A study of metal properties using the method of magnetic memory[J]. Metal Science and Heat Treatment, 1998, 39(9): 35-39. |
| 5 | 邸新杰, 李午申, 白世武, 等. 焊接裂纹的金属磁记忆定量化评价研究[J]. 材料工程, 2006,50(7): 56-60. |
| Di Xin-jie, Li Wu-shen, Bai Shi-wu, et al. Quantitative evaluation study on metal magnetic memory of welding cracks[J]. Journal of Materials Engineering, 2006, 50(7): 56-60. | |
| 6 | 张军, 王彪, 计秉玉. 基于小波变换的套管金属磁记忆检测信号处理[J]. 石油学报, 2006, 27(2): 137-140. |
| Zhang Jun, Wang Biao, Ji Bing-yu. Signal processingfor metal magnetic memory testing of borehole casing based on wavelet transform[J]. Acta Petrolei Sinica,2006, 27(2): 137-140. | |
| 7 | 张军, 王彪, 肖余之. 磁记忆与小波变换相结合的井下套管应力集中早期诊断方法[J]. 吉林大学学报: 工学版, 2007, 37(2): 469-473. |
| Zhang Jun, Wang Biao, Xiao Yu-zhi. Early diagnosis for the stress concentration zone of borehole casing pipe by metal magnetic memory and wavelet transform[J]. Journal of Jilin University(Engineering and Technology Edition), 2007, 37(2): 469-473. | |
| 8 | 刘昌奎, 陶春虎, 陈星, 等. 金属磁记忆检测技术定量评估构件疲劳损伤研究[J]. 材料工程, 2009, 56(8): 33-37. |
| Liu Chang-kui, Tao Chun-hu, Chen Xing, et al. Research on quantitative assessment of fatigue damage bymetal magnetic memory methods[J]. Journal of Materials Engineering, 2009, 56(8): 33-37. | |
| 9 | 张伟, 黄卫民. 基于种群分区的多策略自适应多目标粒子群算法[J/OL]. [2020-09-30]. |
| 10 | 高云龙, 王志豪, 潘金艳, 等. 基于自适应松弛的鲁棒模糊C均值聚类算法[J]. 电子与信息学报, 2020, 42(7):1774-1781. |
| Gao Yun-long, Wang Zhi-hao, Pan Jin-yan, et al. Robust fuzzy C-means based on adaptive relaxation[J]. Journal of Electronics & Information Technology, 2020, 42(7): 1774-1781. | |
| 11 | 周世波, 徐维祥, 徐良坤. 融合密度峰值和空间邻域信息的FCM聚类算法[J]. 仪器仪表学报, 2019, 40(4):137-144. |
| Zhou Shi-bo, Xu Wei-xiang, Xu Liang-kun. ImprovedFCM algorithm based on density peaks and spatial neighborhood information[J]. Chinese Journal of Scientific Instrumen, 2019, 40(4): 137-144. | |
| 12 | 周世波, 唐基宏, 熊振南. 基于优化模糊C均值算法的锚泊船聚集特性[J]. 交通运输工程学报, 2019, 19(6): 137-148. |
| Zhou Shi-bo, Tang Ji-hong, Xiong Zhen-nan. Aggregation characteristics of anchored vessels based on optimized FCM algorithm[J]. Journal of Traffic and Transportation Engineering, 2019, 19(6): 137-148. | |
| 13 | 贾亚飞, 朱永利, 高佳程, 等. 基于样本加权FCM聚类的未知类别局部放电信号识别[J]. 电力自动化设备, 2018, 38(12): 107-112. |
| Jia Ya-fei, Zhu Yong-li, Gao Jia-cheng, et al. Recognition of unknown partial discharge signals based on sample-weighted FCM clustering[J]. Electric Power Automation Equipment, 2018, 38(12): 107-112. | |
| 14 | 易方. 基于ANSYS的管道磁记忆检测技术仿真研究[J].化工机械, 2014, 41(2): 207-210. |
| Yi Fang, Simulation research of pipeline mmm testing technology based on ANSYS[J]. Chemical Engineering & Machinery, 2014, 41(2): 207-210. | |
| 15 | 刘书俊, 蒋明, 张伟明, 等. 基于BP神经网络的磁记忆检测管道缺陷研究[J]. 化工自动化及仪表, 2016, 43(3): 240-243. |
| Liu Shu-jun, Jiang Ming, Zhang Wei-ming, et al. Study on pipeline defect inspection with magnetic memory testing technology based on bp neural network[J]. Control and Instruments in Chemical Industry, 2016, 43(3): 240-243. | |
| 16 | 邢海燕, 葛桦, 李思岐, 等. 基于模糊隶属度最大似然估计的焊缝隐性缺陷磁记忆信号识别[J]. 吉林大学学报: 工学版, 2017, 47(6): 1854-1860. |
| Xing Hai-yan, Ge Hua, Li Si-qi, et al. Hidden defect metal magnetic memory identification for welded joints based on fuzzy membership and maximum likelihood estimation. [J]. Journal of Jilin University(Engineering and Technology Edition), 2017, 47(6): 1854-1860. | |
| 17 | 邢海燕, 喻正帅, 李雪峰, 等. 基于模糊c均值聚类算法的焊缝缺陷等级磁记忆定量识别[J]. 压力容器, 2018, 35(6):57-63. |
| Xing Hai-yan, Yu Zheng-shuai, Li Xue-feng, et al. Quantitative metal magnetic memory identification of weld defect levels based on fuzzy c-means clusering algorithmt[J]. Pressure Vessel Technology, 2018, 35(6): 57-63. | |
| 18 | . 承压设备无损检测 [S]. |
| 19 | Bezdek J C. Pattern Recognition with Fuzzy Objective Function Algorithms[M]. Boston, MA:Springer, 1981. |
| [1] | 罗巍,卢博,陈菲,马腾. 基于PSO-SVM及时序环节的数控刀架故障诊断方法[J]. 吉林大学学报(工学版), 2022, 52(2): 392-399. |
| [2] | 杜常清,曹锡良,何彪,任卫群. 基于混合粒子群算法的双离合变速器参数优化设计[J]. 吉林大学学报(工学版), 2020, 50(5): 1556-1564. |
| [3] | 马芳武,韩丽,吴量,李金杭,杨龙帆. 基于遗传与粒子群算法的隔振平台减振性能优化[J]. 吉林大学学报(工学版), 2020, 50(5): 1608-1616. |
| [4] | 刘富, 兰旭腾, 侯涛, 康冰, 刘云, 林彩霞. 基于优化k-mer频率的宏基因组聚类方法[J]. 吉林大学学报(工学版), 2018, 48(5): 1593-1599. |
| [5] | 臧国帅, 孙立军. 基于惰性弯沉点的刚性下卧层深度设置方法[J]. 吉林大学学报(工学版), 2018, 48(4): 1037-1044. |
| [6] | 邢海燕, 葛桦, 李思岐, 杨文光, 孙晓军. 基于模糊隶属度最大似然估计的焊缝隐性缺陷磁记忆信号识别[J]. 吉林大学学报(工学版), 2017, 47(6): 1854-1860. |
| [7] | 于繁华, 刘仁云, 张义民, 张晓丽, 孙秋成. 机械零部件动态可靠性稳健优化设计的群智能算法[J]. 吉林大学学报(工学版), 2017, 47(6): 1903-1908. |
| [8] | 孙亮, 徐海浪, 葛宏伟. 保证全局收敛的随机粒子群新算法[J]. 吉林大学学报(工学版), 2017, 47(2): 615-623. |
| [9] | 于繁华, 刘仁云, 张义民, 孙秋成, 张晓丽. 机械结构动态可靠性设计的智能计算方法[J]. 吉林大学学报(工学版), 2016, 46(4): 1269-1275. |
| [10] | 张静, 刘向东. 混沌粒子群算法优化最小二乘支持向量机的混凝土强度预测[J]. 吉林大学学报(工学版), 2016, 46(4): 1097-1102. |
| [11] | 季彦婕, 陈晓实, 王炜, 胡波. 基于小波变换和粒子群小波神经网络组合模型的有效停车泊位短时预测[J]. 吉林大学学报(工学版), 2016, 46(2): 399-405. |
| [12] | 刘云, 刘富, 侯涛, 张潇. 优化核参数的模糊C均值聚类算法[J]. 吉林大学学报(工学版), 2016, 46(1): 246-251. |
| [13] | 高明亮, 于生宝, 郑建波, 徐畅, 张堃, 栾卉. PSBP在高密度电阻率法二维反演中的应用[J]. 吉林大学学报(工学版), 2015, 45(6): 2026-2033. |
| [14] | 刘红,孙爽滋,王庆元,李延忠. 基于PSO的模拟电路故障信息特征提取[J]. 吉林大学学报(工学版), 2015, 45(2): 675-680. |
| [15] | 姜万录,卢传奇,朱勇. 基于HHT和模糊C均值聚类的轴向柱塞泵故障识别[J]. 吉林大学学报(工学版), 2015, 45(2): 429-436. |
|
||