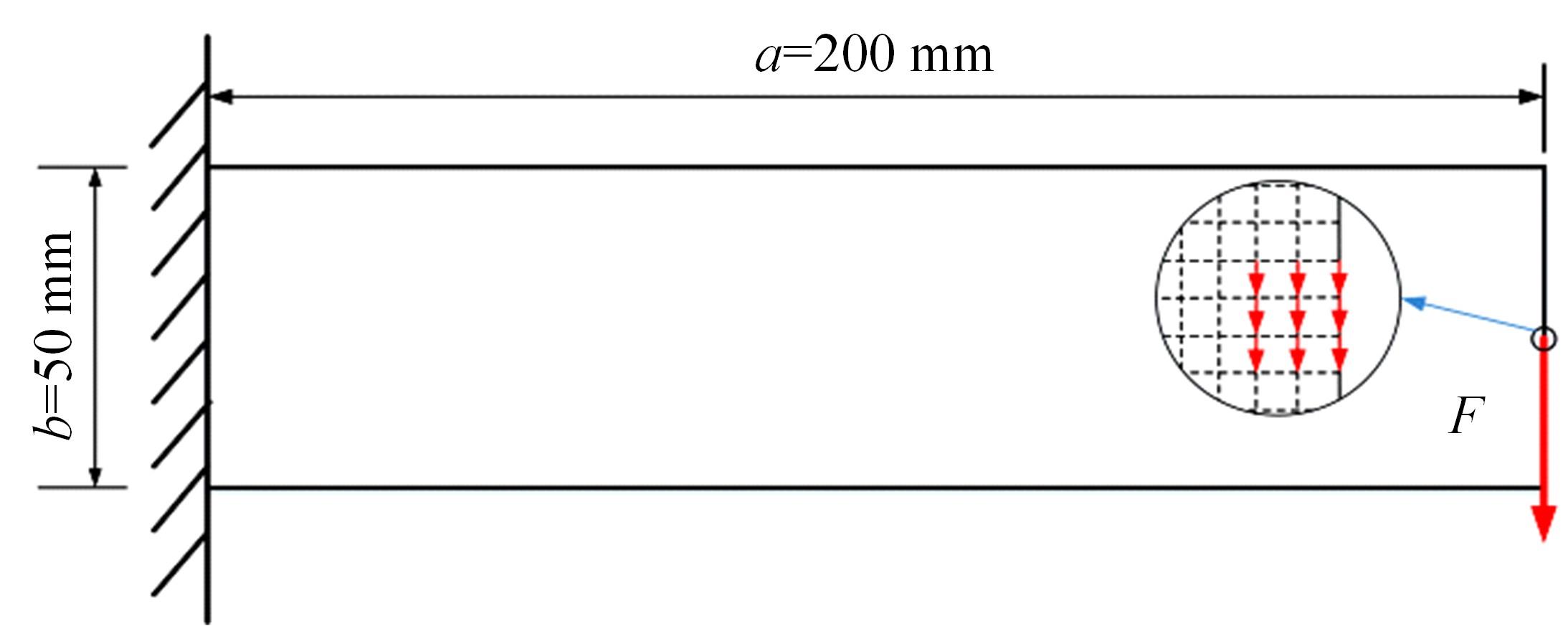
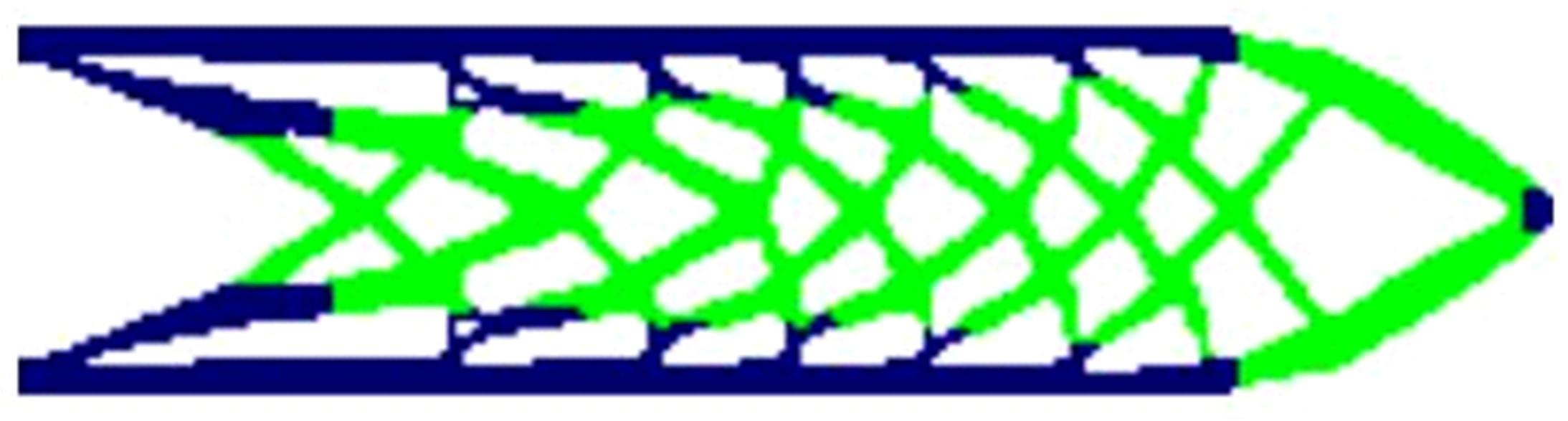
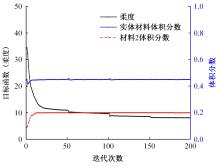
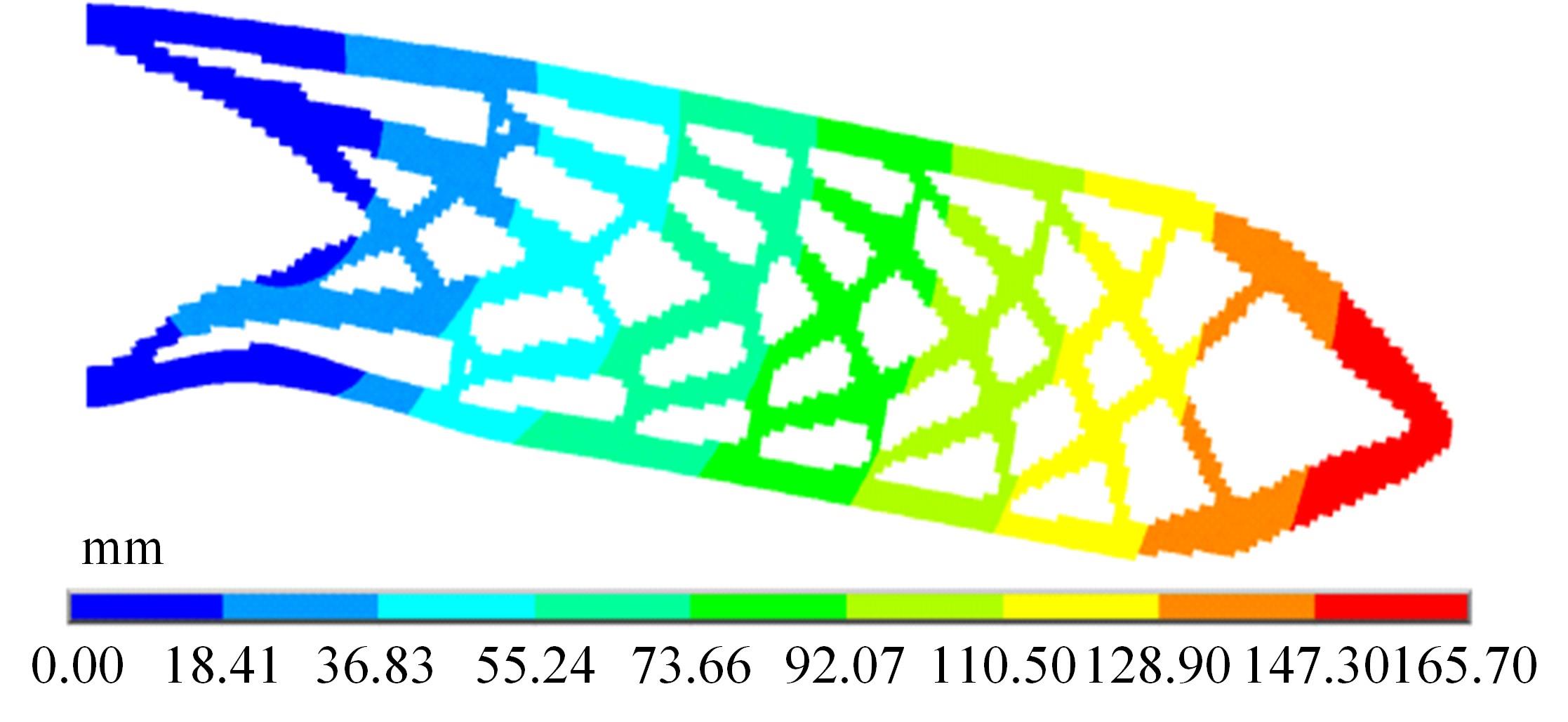
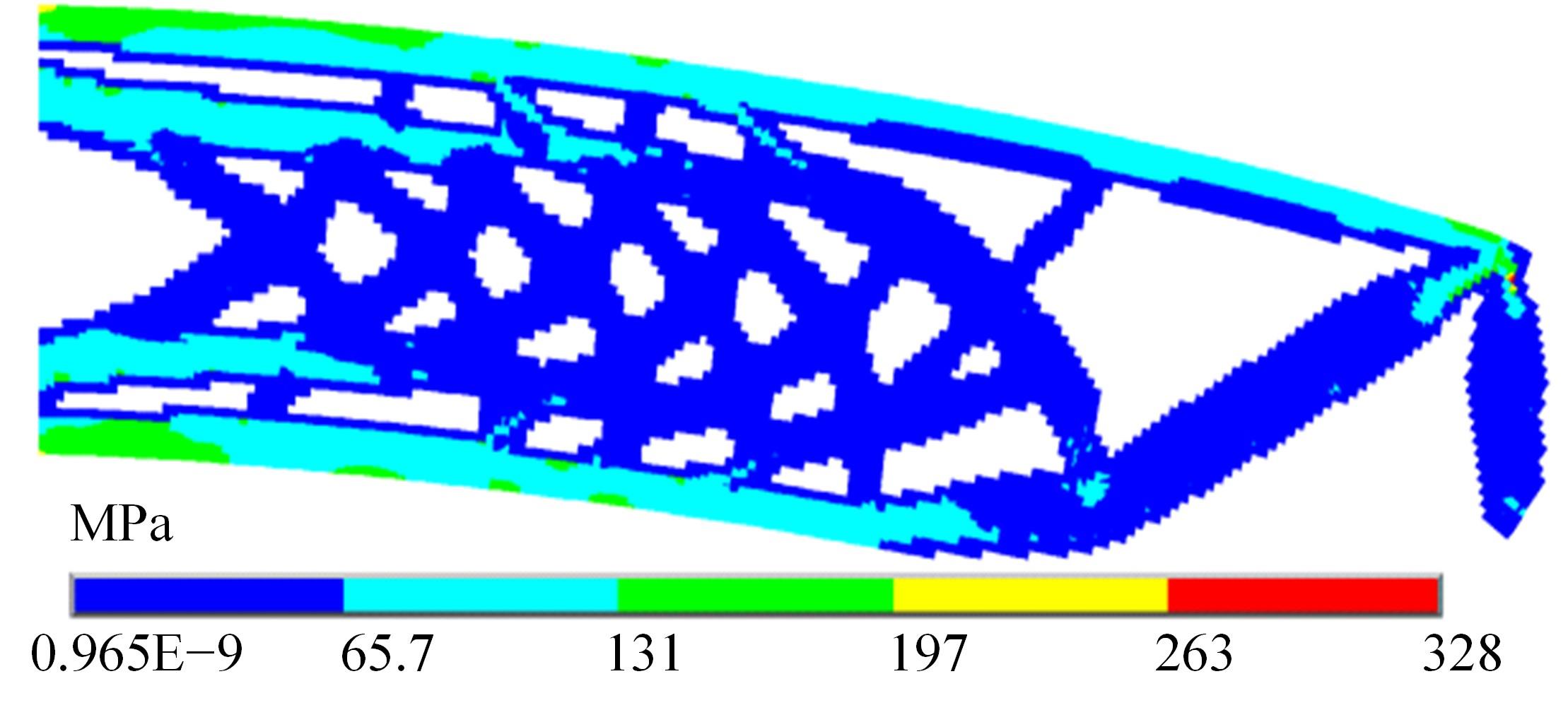
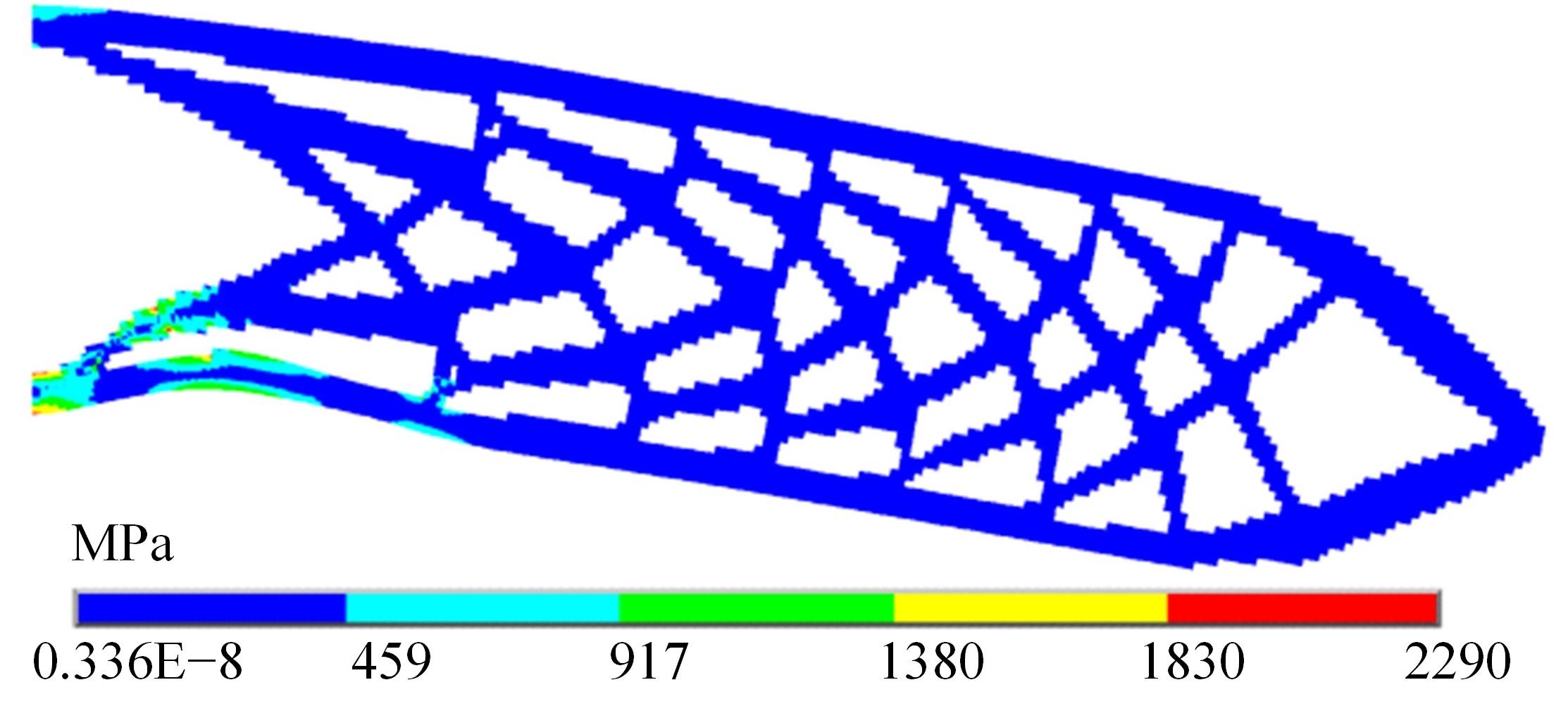
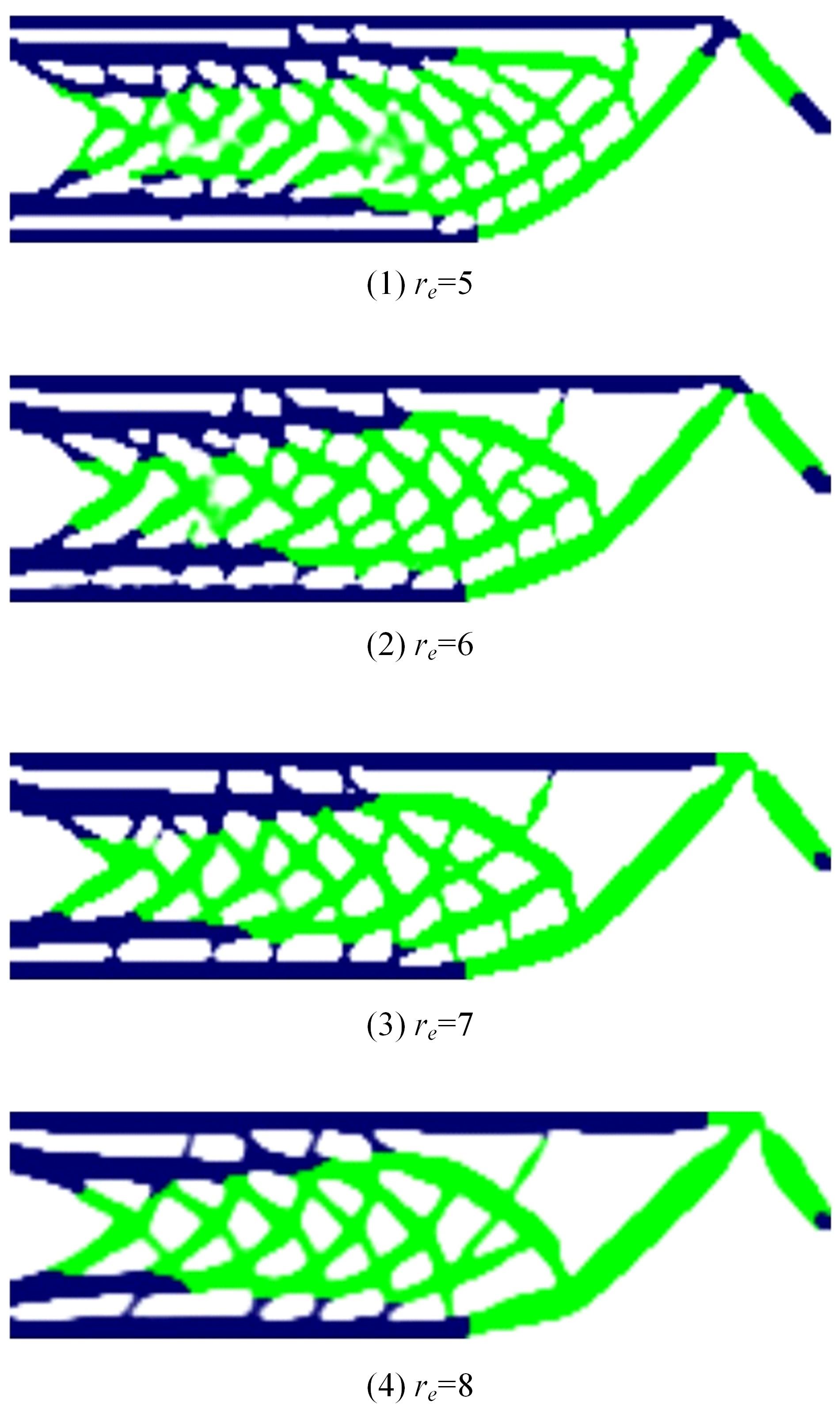
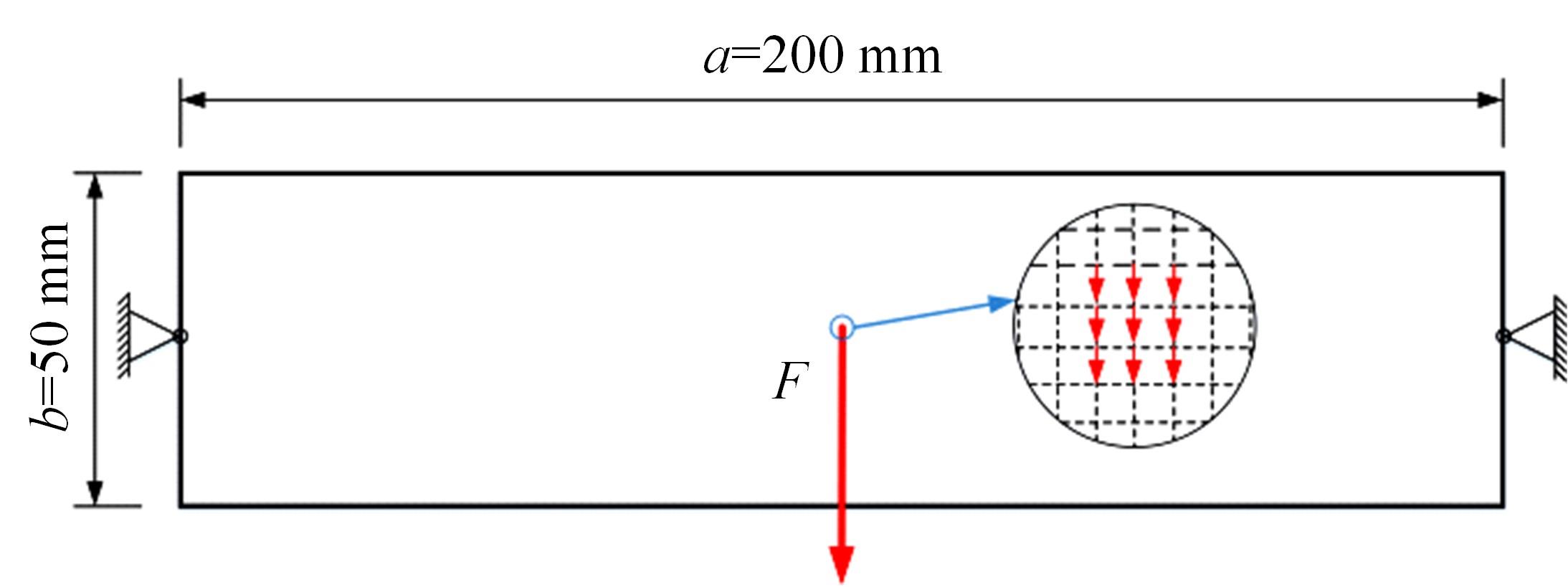
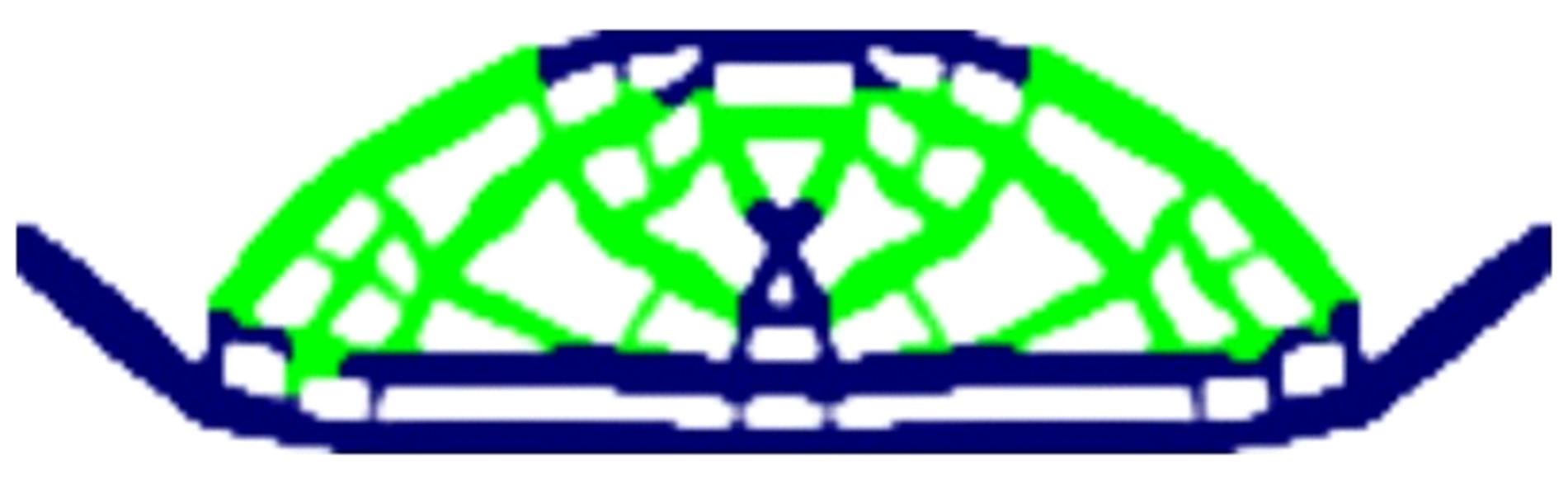
Journal of Jilin University(Engineering and Technology Edition) ›› 2024, Vol. 54 ›› Issue (10): 2754-2763.doi: 10.13229/j.cnki.jdxbgxb.20221624

Previous Articles    

Topology optimization design of multiphase porous structures considering geometric nonlinearity

Huan-lin ZHOU1(),Xin GUO1,Xuan WANG1,2(),Li-xue FANG1,Kai LONG3   

  1. 1.College of Civil Engineering，Hefei University of Technology，Hefei 230009，China
    2.School of Mechanical Engineering，Tianjin University，Tianjin 300072，China
    3.State Key Laboratory for Alternate Electrical Power System with Renewable Energy Sources，North China Electric Power University，Beijing 102206，China
  • Received:2022-12-25 Online:2024-10-01 Published:2024-11-22
  • Contact: Xuan WANG E-mail:zhouhl@hfut.edu.cn;xuanwang@hfut.edu.cn

RICH HTML

 0   

PDF (PC)

200

Abstract:

A topology optimization method of multiphase porous structures considering geometric nonlinearity effects is proposed based on SIMP interpolation model. The multi-phase porous structure is formed by controlling the local volume fraction of different material phases. To reduce the number of constraints in the optimization problem， the p-norm is used to aggregate multiple local volume constraints into a global constraint function. The additional hyperelastic technique is used to avoid mesh distortion under large geometric deformation. Finally， two optimization examples are presented to verify the effectiveness of the proposed method. The optimization results show that the proposed method can achieve reasonable distribution among different material phases， and the displacement and stress of the porous structures considering the nonlinear effect are smaller. Compared with the single material structure， the porous structures composed of multi-materials has better mechanical properties.

Key words: mechanical engineering, porous structure, geometric nonlinearity, topology optimization, local volume constraint, multiphase materials

CLC Number: 

  • O342

Fig.1

Design domain of cantilever beam"

Fig.2

Topology optimization results of porous structures of two-phase materials based on linear elastic theory"

Fig.3

Topology optimization results of porous structures of two-phase materials considering nonlinear"

Fig.4

Iterative histories of objective function and volume fraction considering nonlinear theory"

Fig.5

Displacement cloud diagram of nonlinear porous structure"

Fig.6

Displacement cloud diagram of linear poroustruture"

Fig.7

Stress cloud diagram of nonlinear porous structure"

Fig.8

Stress cloud diagram of linear porous structure"

Fig.9

Topology optimization results of porous structures of two-phase materials under different local volume filter radii"

Table 1

Objective function and volume fraction underdifferent local volume filter radius"

Casesre柔度实体体积分数材料2体积分数
Case 159.8320.4280.1993
Case 268.8420.4350.1973
Case 378.3570.4440.1986
Case 488.0860.4500.1999

Fig.10

Design domain of two point fixed structure"

Fig.11

Topology optimization results of porous structures of two-phase materials based on linear elastic theory"

Fig.12

Topology optimization results of porous structures of two-phase materials considering geometric nonlinear"

Fig.13

Topology optimization results of porous structures of three-phase materials based on linear elastic theory"

Fig.14

Topology optimization results of porous structures of three-phase materials considering geometric nonlinear theory"

Fig.15

Iterative histories of objective function and volume fraction considering geometric nonlinear theory"

Table 2

Compliance function and maximum displacement for different material phases"

材料相数柔度实体体积分数最大位移/mm
单相1.0230.4004.100
两相0.8500.4003.405
三相0.7640.4003.055
1 Nazir A, Jeng J Y. Buckling behavior of additively manufactured cellular columns: experimental and simulation validation[J]. Materials & Design, 2020, 186: No.108349.
2 Clausen A, Aage N, Sigmund O. Exploiting additive manufacturing infill in topology optimization for improved buckling load[J]. Engineering, 2016, 2(2): 250-257.
3 Bai J, Zuo W. Hollow structural design in topology optimization via moving morphable component method[J]. Structural and Multidisciplinary Optimization, 2020, 61(1): 187-205.
4 Wu J, Niels A, Rudiger W, et al. Infill optimization for additive manufacturing-approaching bone-like porous structures[J]. IEEE Transactions on Visualization and Computer Graphics, 2017,4(2): 1127-1140.
5 Wu J, Clausen A, Sigmund O. Minimum compliance topology optimization of shell-infill composites for additive manufacturing[J]. Computer Methods in Applied Mechanics and Engineering, 2017, 326: 358-375.
6 Liu C, Du Z, Zhang W, et al. Additive manufacturing-oriented design of graded lattice structures through explicit topology optimization[J]. Journal of Applied Mechanics, 2017, 84(8): No.081008.
7 Liu C, Du Z, Zhu Y, et al. Optimal design of shell-graded-infill structures by a hybrid MMC-MMV approach[J]. Computer Methods in Applied Mechanics and Engineering, 2020, 369: No. 113187.
8 Das S, Sutradhar A. Multi-phys ics topology optimization of functionally graded controllable porous structures: application to heat dissipating problems[J]. Materials & Design, 2020, 193: No.108775.
9 Hoang V N, Tran P, Nguyen N L, et al. Adaptive concurrent topology optimization of coated structures with nonperiodic infill for additive manufacturing[J]. Computer-Aided Design, 2020, 129: No.102918.
10 Hoang V N, Wang X, Nguyen-Xuan H. A three-dimensional multiscale approach to optimal design of porous structures using adaptive geometric components[J]. Composite Structures, 2021, 273: No.114296.
11 Dou S G. A projection approach for topology optimization of porous structures through implicit local volume control[J]. Structural and Multidisciplinary Optimization, 2020, 62(2): 835-850.
12 Long K, Chen Z, Zhang C W, et al. An aggregation-free local volume fraction formulation for topological design of porous structure[J]. Materials, 2021, 14(19): No.5726.
13 Zhao Z, Zhang X S. Design of graded porous bone-like structures via a multi-material topology optimization approach[J]. Structural and Multidisciplinary Optimization, 2021, 64(2): 677-698.
14 胡传丰, 任靖雯, 胡慧,等. 基于等几何分析的参数多孔结构拓扑优化[J]. 吉林大学学报:理学版, 2021, 59(1): 65-76.
Hu Chuan-feng, Ren Jing-wen, Hu Hui, et al. Topology optimization for parametric porous structure based on iso-geometric analysis[J]. Journal of Jilin University Science Edition, 2021, 59(1): 65-76.
15 Garaigordobil A, Ansola R, Querin O M, et al. Infill topology optimization of porous structures with discrete variables by the sequential element rejection and admission method[J]. Engineering Optimization, 2021, 55(3): 457-475.
16 Gan N, Wang Q. Topology optimization design of porous infill structure with thermo-mechanical buckling criteria[J]. International Journal of Mechanics and Materials in Design, 2022, 18(2): 267-288.
17 Huang J, Xu S, Ma Y, et al. A topology optimization method for hyperelastic porous structures subject to large deformation[J]. International Journal of Mechanics and Materials in Design, 2022, 18(2): 289-308.
18 Xue R, Liu C, Zhang W, et al. Explicit structural topology optimization under finite deformation via moving morphable void (MMV) approach[J]. Computer Methods in Applied Mechanics and Engineering, 2019, 344: 798-818.
19 文桂林, 刘杰, 陈梓杰, 等. 非线性连续体拓扑优化方法综述[J]. 力学学报, 2022, 54(10): 2659-2675.
Wen Gui-lin, Liu Jie, Chen Zi-jie, et al. A survey of nonlinear continuum topology optimization methods[J]. Chinese Journal of Theoretical and Applied Mechanics, 2022, 54(10): 2659-2675 .
20 陆念力,张宏生. 计及纵横变形效应的几何非线性三次样条梁单元[J]. 吉林大学学报:工学版, 2010, 40(3): 745-751.
Lu Nian-li, Zhang Hong-sheng. Geometric nonlinear cubic spline beam element with lateral and axial deformation effects[J]. Journal of Jilin University(Engineering and Technology Edition), 2010, 40(3): 745-751.
21 朱本亮, 张宪民, 李海, 等. 基于节点密度插值的多材料柔顺机构拓扑优化[J]. 机械工程学报, 2021, 57(15): 53-61.
Zhu Ben-liang, Zhang Xian-min, Li Hai, et al. Topology optimization of multi-material compliant mechanisms using node-density interpolation scheme[J]. Journal of Mechanical Engineering, 2021, 57(15): 53-61.
22 Zuo W, Saitou K. Multi-material topology optimization using ordered SIMP interpolation[J]. Structural and Multidisciplinary Optimization, 2017, 55(2): 477-491.
23 王选,胡平,龙凯.考虑嵌入移动孔洞的多相材料布局优化[J].力学学报,2019,51(3): 852-862.
Wang Xuan, Hu Ping, Long Kai. Multiphase material layout optimization considering embedding movable holes[J]. Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(3): 852-862.
24 Guo X, Zhang W, Zhong W. Stress-related topology optimization of continuum structures involving multi-phase materials[J]. Computer Methods in Applied Mechanics and Engineering, 2014, 268: 632-655.
25 Lazarov B S, Sigmund O. Filters in topology optimization based on Helmholtz‐type differential equations[J]. International Journal for Numerical Methods in Engineering, 2011, 86(6): 765-781.
26 Wang F, Lazarov B S, Sigmund O. On projection methods, convergence and robust formulations in topology optimization[J]. Structural and Multidisciplinary Optimization, 2011, 43(6): 767-784.
27 Luo Y J, Wang M Y, Kang Z. Topology optimization of geometrically nonlinear structures based on an additive hyperelasticity technique[J]. Computer Methods in Applied Mechanics and Engineering, 2015, 286: 422-441.
28 Chen Q, Zhang X M, Zhu B L. A 213-line topology optimization code for geometrically nonlinear structures[J]. Structural and Multidisciplinary Optimization, 2019, 59(5): 1863-1879.
29 Buhl T, Pedersen C B W, Sigmund O. Stiffness design of geometrically nonlinear structures using topology optimization[J]. Structural and Multidisciplinary Optimization, 2000,19(2): 93-104.
30 Wang F, Lazarov B S, Sigmund O, et al. Interpolation scheme for fictitious domain techniques and topology optimization of finite strain elastic problems[J]. Computer Methods in Applied Mechanics and Engineering, 2014, 276: 453-472.
[1] Lei SHANG,Ping YANG,Xiang-guo YANG,Jian-xin PAN,Jun YANG,Meng-ru ZHANG. Temperature control of proton exchange membrane fuel cell thermal management system based on APSO-BP-PID control strategy [J]. Journal of Jilin University(Engineering and Technology Edition), 2024, 54(9): 2401-2413.
[2] Lin JIANG,Guo-long LI,Shi-long WANG,Kai XU,Zhe-yu LI. Thermal expansion error modeling of feed axis based on principal component regression [J]. Journal of Jilin University(Engineering and Technology Edition), 2024, 54(8): 2149-2155.
[3] Ze-qiang ZHANG,Can WANG,Jun-qi LIU,Dan JI,Si-lu LIU. Parallel row ordering problem based on improved sparrow search algorithm [J]. Journal of Jilin University(Engineering and Technology Edition), 2024, 54(7): 1851-1861.
[4] Cai-xia SHU,Jia YANG,Qing-xi LIAO,Xing-yu WAN,Jia-cheng YUAN. Design and experiment of diversion type double-cylinder cyclone separation system for rapeseed combine harvester [J]. Journal of Jilin University(Engineering and Technology Edition), 2024, 54(6): 1807-1820.
[5] Li HUI,Lei JIN,Wan-wan SONG,Song ZHOU,Jin-lan AN. Crack growth rate of SMA490BW steel in different welding areas for bogie [J]. Journal of Jilin University(Engineering and Technology Edition), 2024, 54(3): 650-656.
[6] Zhi-jun YANG,Chi ZHANG,Guan-xin HUANG. Mechanical model of rigid⁃flexible coupling positioning stage based on floating coordinate method [J]. Journal of Jilin University(Engineering and Technology Edition), 2024, 54(2): 385-393.
[7] Lin-rong SHI,Wu-yun ZHAO. Design and test of rolling spoon type flaxes precision hole sower for caraway in northwest cold and arid agricultural region [J]. Journal of Jilin University(Engineering and Technology Edition), 2023, 53(9): 2706-2717.
[8] Bo-sen CHAI,Guang-yi WANG,Dong YAN,Guo-ren ZHU,Jin ZHANG,Heng-sheng LYU. Numerical simulation of cavitation in torque converter and analysis of its influence on performance [J]. Journal of Jilin University(Engineering and Technology Edition), 2023, 53(8): 2236-2244.
[9] Guo-hui CHEN,Ye-yin XU,Ying-hou JIAO. Meshing stiffness calculation and vibration analysis of helical gear considering deflection [J]. Journal of Jilin University(Engineering and Technology Edition), 2023, 53(7): 1902-1910.
[10] Feng WANG,Shuang-rui LIU,Jia-ying WANG,Jia-ling SONG,Jun WANG,Jiu-peng ZHANG,Xiao-ming HUANG. Size and shape effects of wind drag coefficients for porous structures [J]. Journal of Jilin University(Engineering and Technology Edition), 2023, 53(6): 1677-1685.
[11] Sheng LI,Jia ZHU,De-hui HUANG,Cun-fu CHEN,Hong-qing FEI,Wei FENG,Xing-jun HU. Structural parameters optimization of louver fins of air⁃cooled charge air cooler [J]. Journal of Jilin University(Engineering and Technology Edition), 2023, 53(4): 998-1006.
[12] Jian WANG,Wei YU,Bin WANG. Effects of methanol substitution percent on combustion and emission of diesel engines under plateau condition [J]. Journal of Jilin University(Engineering and Technology Edition), 2023, 53(4): 954-963.
[13] Li-juan YU,Yang AN,Jia-long HE,Guo-fa LI,Sheng-xu WANG. Research progress and development trend of extrapolation method in electromechanical equipment load spectrum [J]. Journal of Jilin University(Engineering and Technology Edition), 2023, 53(4): 941-953.
[14] Bo-sen CHAI,Dong YAN,Guang-yi WANG,Wen-jie ZUO. Three-dimensional vortex characteristic analysis and simulation evaluation of peach cavity hydrodynamic coupling under braking condition [J]. Journal of Jilin University(Engineering and Technology Edition), 2023, 53(11): 3045-3055.
[15] Shu-yang SUN,Wei-bin CHENG,Hao-zhen ZHANG,Xiang-ping DENG,Hong QI. Deep-learning-based two-stage approach for real-time explicit topology optimization [J]. Journal of Jilin University(Engineering and Technology Edition), 2023, 53(10): 2942-2951.
Viewed
Full text


Abstract

Cited
  Shared   
  Discussed   
No Suggested Reading articles found!
Copyright © Journal of Jilin University(Engineering and Technology Edition), All Rights Reserved.
Tel: +86-431-85095297　Fax: +86-431-85094074　E-mail: xbgxb@jlu.edu.cn
Powered by Beijing Magtech Co. Ltd