在役混凝土T梁疲劳刚度退化及寿命预测方法

doi:10.13229/j.cnki.jdxbgxb.20211238

摘要/Abstract

摘要：

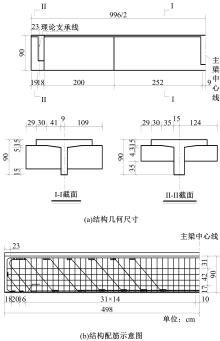
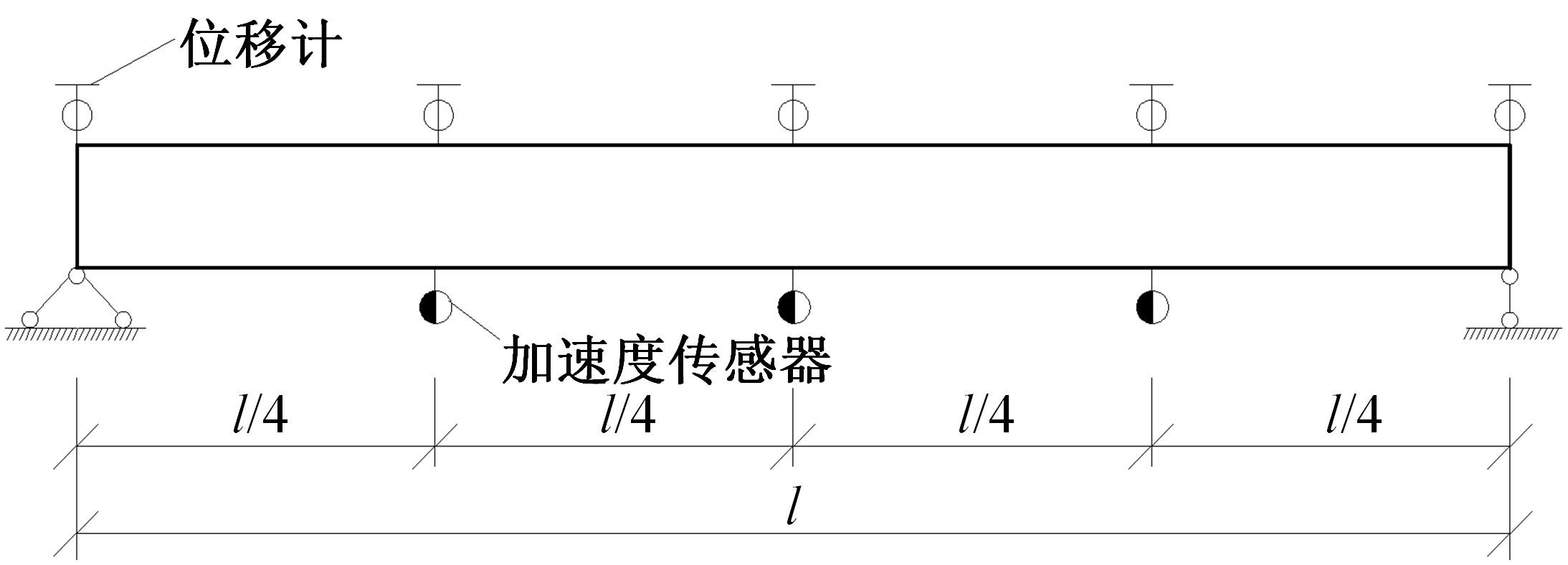
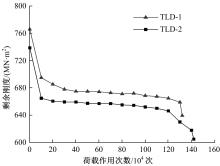
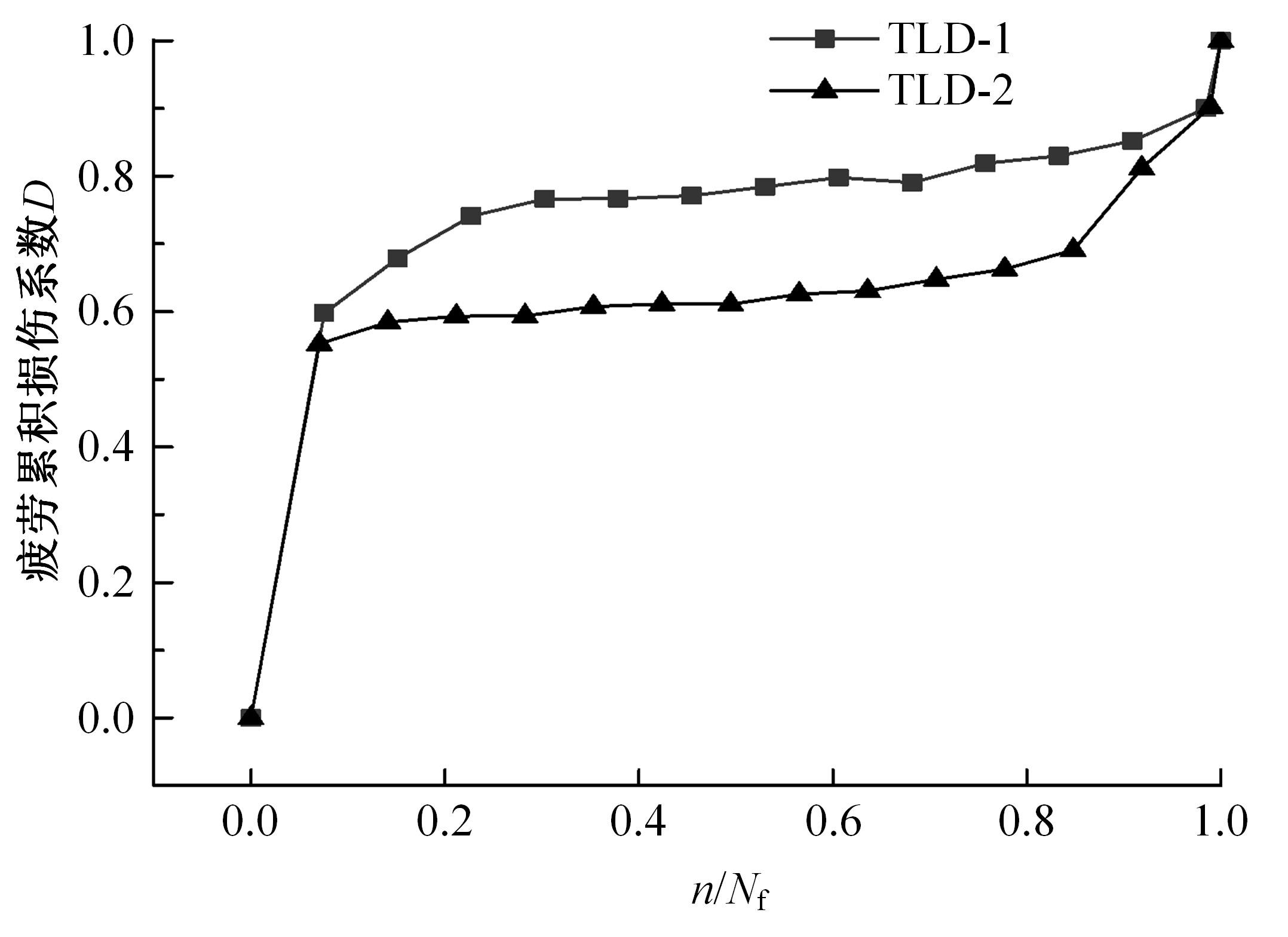
为获取在役混凝土T梁疲劳刚度退化规律，开展疲劳寿命预测，基于损伤力学理论构建了考虑开裂损伤的混凝土T梁阶梯刚度模型，通过对3根10 m钢筋混凝土T梁足尺模型进行静力和疲劳破坏试验，获取了疲劳剩余刚度随荷载作用次数的演化规律。引入疲劳损伤系数和刚度退化系数，建立了在役混凝土T梁疲劳寿命预测模型。分析结果表明：随着荷载作用次数的增加，桥梁剩余刚度呈现三阶段衰减，其中疲劳初期和后期阶段衰减较快，但占总寿命比重相对较小，而疲劳中期阶段呈线性稳定退化，约占疲劳总寿命的80%以上，为桥梁服役的主要阶段，疲劳破坏时剩余刚度约为初始刚度的82.7%。最终，针对在役混凝土T梁桥工作性状，提出了在役钢筋混凝土梁桥寿命预测方法，相关研究成果可为此类桥梁寿命预测研究提供理论支持。

关键词: 桥梁工程, 在役混凝土T梁, 疲劳寿命, 阶梯刚度模型, 累积损伤系数

Abstract:

In order to obtain the fatigue stiffness degradation law of in-service concrete T-beams and carry out fatigue life prediction. Based on the theory of damage mechanics， a stepped stiffness model of concrete T-beams including cracking damage was constructed. Through the full-scale model of three 10 m concrete T beams， static and fatigue failure tests were carried out to obtain the evolution law of fatigue residual stiffness with the number of loads. The fatigue damage coefficient and stiffness degradation coefficient were introduced to establish a concrete T beam in service fatigue life prediction model. The analysis results show that with the increase of load， the residual stiffness of the bridge exhibits three-stage decay， in which the initial and later stages of fatigue decay rapidly， but account for a relatively small proportion of the whole life. The result shows that more than 80% of the whole service life is the main stage of bridge service， it is about 82.7% of the initial stiffness at the time of fatigue failure. Finally， according to the working behavior of in-service concrete T-girder bridges， a life prediction method for in-service reinforced concrete girder bridges is proposed， the related research results can provide theoretical support for the study of life prediction of such bridges.

Key words: bridge engineering, in-service concrete T-beam, fatigue life, stepped stiffness model, cumulative damage coefficient

中图分类号:

U448.38

左新黛,张劲泉,赵尚传. 在役混凝土T梁疲劳刚度退化及寿命预测方法[J]. 吉林大学学报(工学版), 2023, 53(9): 2563-2572.

Xin-dai ZUO,Jin-quan ZHANG,Shang-chuan ZHAO. Fatigue stiffness degradation and life prediction method of in⁃service concrete T⁃beams[J]. Journal of Jilin University(Engineering and Technology Edition), 2023, 53(9): 2563-2572.

图/表 18

图1

图2

图3

图4

表1

图5

表2

疲劳试验加载参数"

试验梁编号	$P m i n$ /kN	$P m a x$ /kN	应力幅/kN
TLD-1	50	370	320
TLD-2	50	370	320

表2

图6

图7

图8

表3

图9

表4

表5

不同荷载作用次数下试验梁基频实测值与剩余刚度计算值"

荷载循环次数n/10⁴ 次	TLD-1					TLD-2
荷载循环次数n/10⁴ 次	x₁/m	x₂/m	基频f/Hz	剩余刚度比 $η n$	剩余刚度 $B n$ /（MN·m²）	x₁/m	x₂/m	基频f/Hz	剩余刚度比 $η n$	剩余刚度 $B n$ /（MN·m²）
0.0	0.0	0.0	15.13	1.000	765.712	0.0	0.0	14.96	1.000	738.627
10.0	4.1	4.1	14.94	0.907	694.803	4.1	4.2	14.94	0.900	664.674
20.0	3.9	3.9	14.85	0.895	685.169	4.0	4.0	14.88	0.894	660.385
30.0	3.7	3.6	14.74	0.885	677.781	4.0	3.9	14.86	0.892	659.215
40.0	3.7	3.5	14.71	0.881	674.787	3.5	3.7	14.75	0.892	659.165
50.0	3.5	3.4	14.66	0.881	674.727	3.4	3.4	14.68	0.890	657.288
60.0	3.4	3.2	14.61	0.880	674.200	3.2	3.2	14.62	0.889	656.816
70.0	3.3	3.1	14.57	0.878	672.651	3.1	3.0	14.58	0.889	656.865
80.0	3.3	3.1	14.56	0.876	671.021	2.9	3.0	14.54	0.887	654.868
90.0	3.1	3.0	14.52	0.877	671.895	2.9	2.8	14.51	0.886	654.229
100.0	2.8	2.6	14.40	0.873	668.518	2.8	2.8	14.48	0.883	651.935
110.0	2.8	2.6	14.39	0.871	667.220	2.8	2.6	14.44	0.880	649.888
120.0	2.8	2.6	14.37	0.868	664.627	2.8	2.6	14.41	0.875	646.124
130.0	1.8	1.5	14.11	0.860	658.861	2.3	2.2	14.16	0.853	629.929
132.0	1.6	1.5	13.90	0.835	639.407	—	—	—	—	—
140.0	—	—	—	—	—	2.1	1.8	13.98	0.836	617.775
141.5	—	—	—	—	—	2.1	1.8	13.85	0.819	604.714

表5

图10

表6

试验梁疲劳试验结果"

试验梁编号	初始刚度 $B 0$ /（MN·m²）	破坏刚度 $B N f$ /（MN·m²）	刚度比 $B N f / B 0$	刚度退化率k/（10^-4 MN·m²）	疲劳寿命N_f/10⁴ 次
TLD-1	765.712	639.407	0.835	0.271	132.0
TLD-2	738.672	604.714	0.819	0.241	141.5

表6

图11

表7

参考文献 20

1	交通运输部. 2019年年交通运输行业发展统计公报[R]. 北京:交通运输部, 2020.
2	宋秀华, 肖新辉, 鲁乃唯. 基于疲劳损伤的中小跨径桥梁限载取值研究[J]. 交通科学与工程, 2019, 35(2): 58-63.
	Song Xiu-hua, Xiao Xin-hui, Lu Nai-wei. Study on vehicle load limit of medium and small span bridges based on fatigue damage[J]. Journal of Transport Science and Engineering, 2019,35(2): 58-63.
3	卫军, 杜永潇, 梁曼舒. 梁结构疲劳刚度退化对模态频率的影响[J] .浙江大学学报:工学版, 2019, 53(5): 899-909.
	Wei Jun, Du Yong-xiao, Liang Man-shu. Influence of fatigue stiffness degradation for beam structure on modal frequency[J]. Journal of Zhejiang University (Engineering Science), 2019, 53(5): 899-909.
4	刘芳平, 易文韬. 钢筋混凝土梁基于疲劳刚度退化的承载力退化模型研究[J]. 建筑结构, 2020, 50(22): 99-104, 66.
	Liu Fang-ping, Yi Wen-tao. Research on bearing capacity degr8dation model of reinforced concrete beams based on fatigue stiffness degradation[J]. Building Structure, 2020,50(22): 99-104, 66.
5	汪炳, 黄侨, 刘小玲. 组合梁疲劳后的刚度退化规律及计算模型[J]. 振动与冲击, 2021, 40(6): 265-271.
	Wang Bing, Huang Qiao, Liu Xiao-ling. Stiffness degradation and its calculation model for composite beams after fatigue[J]. Journal of Vibration and Shock, 2021, 40(6): 265-271.
6	周虎, 肖勇刚, 谭斌. 基于断裂力学的混凝土桥梁疲劳损伤及寿命评估分析[J]. 湖南城市学院学报: 自然科学版, 2018, 27(4): 6-10.
	Zhou Hu, Xiao Yong-gang, Tan Bin. Fatigue damage and life evaluation of concrete bridges based on fracture mechanics[J]. Journal of Hunan City University (Natural Science), 2018, 27(4): 6-10.
7	陈万. 重载交通作用下桥梁结构的疲劳损伤数值分析[D].邯郸: 河北工业大学土木工程学院, 2015.
	Chen Wan. Numerical analysis on fatigue damage of bridge caused by heavy load traffic[D]. Handan: School of Civil Engineering, Hebei University of Technology, 2015.
8	赵少杰, 任伟新. 超限超载交通对桥梁疲劳损伤及可靠度的影响[J]. 中南大学学报: 自然科学版, 2017, 48(11): 3044-3050.
	Zhao Shao-jie, Ren Wei-xin. Effect of overrun and overloaded vehicles on fatigue damage and reliability of highway bridges[J]. Journal of Central South University (Science and Technology), 2017, 48(11): 3044-3050.
9	Natário F, Fernández R M, Muttoni A. Experimental investigation on fatigue of concrete cantilever bridge deck slabs subjected to concentrated loads[J]. Engineering Structures, 2015, 89: 191-203.
10	Liu Fang-ping, Zhou Jian-ting, Yan Lei. Study of stiffness and bearing capacity degradation of reinforced concrete beams under constant-amplitude fatigue[J]. PLoS ONE, 2018, 13(3): No.e0192797.
11	朱红兵. 公路钢筋混凝土简支梁桥疲劳试验与剩余寿命预测方法研究[D]. 长沙: 中南大学土木工程学院, 2011.
	Zhu Hong-Bing. Method and experiment research on highway reinforced concrete simply-supported girder bridge's fatigue residual service life forecast[D]. Changsha: School of Civil Engineering, Central South University, 2011.
12	刘芳平, 周建庭. 基于疲劳应变演化的混凝土弯曲强度退化分析[J]. 中国公路学报, 2017, 30(4): 97-105.
	Liu Fang-ping, Zhou Jian-ting. Concrete bending strength degradation analysis based on fatigues strain evolution[J]. China Journal of Highway and Transport, 2017, 30(4): 97-105.
13	Cheng L J. Flexural fatigue analysis of a CFRP form reinforced concrete bridge deck[J]. Composite Structures, 2011, 93(11):2895-2902.
14	Neild S A, Williams M S, Mcfadden P D. Nonlinear vibration characteristics of damaged concrete beams[J]. Journal of Structural Engineering ASCE, 2003, 129(2): 260-268.
15	曹晖, 郑星, 华建民, 等. 基于非线性振动特性的预应力混凝土梁损伤识别[J]. 工程力学, 2014, 31(2): 190-194.
	Cao Hui, Zheng Xing, Hua Jian-min, et al. Damage detection of prestressed concrete beams based on non-linger dynamic characteristics[J]. Engineering Mechanics, 2014, 31(2): 190-194.
16	卫军, 杜永潇. 基于固有频率的梁结构疲劳损伤演化规律[J]. 中南大学学报: 自然科学版, 2019, 50(8): 1866-1875.
	Wei Jun, Du Yong-xiao. Fatigue damage evolution of Timoshenko beams based on natural frequency[J]. Journal of Central South University (Science and Technology), 2019, 50(8): 1866-1875.
17	朱红兵, 赵耀, 李秀, 等. 疲劳荷载作用下钢筋混凝土梁的刚度退化规律及计算公式[J].土木建筑与环境工程, 2014, 36(2): 1-13.
	Zhu Hong-bing, Zhao Yao, Li Xiu, et al. Reinforced concrete beam's stiffness degeneration regulation and its calculation formula under the action of fatigue load[J]. Journal of Civil, Architectural & Environment Engineering, 2014, 36(2): 1-13.
18	姚恒盈. 装配式预应力混凝土箱梁静动刚度足尺试验全过程分析[D]. 西安:长安大学公路学院, 2020.
	Yao Heng-ying. Dynamic and static stiffness analysis of full-scale prefabricated prestressed concrete girder[D]. Xi′an: School of Highway, Chang'an University, 2020.
19	廉伟, 姚卫星.复合材料层压板剩余刚度-剩余强度关联模型[J]. 复合材料学报, 2008, 25(5): 151-156.
	Lian Wei, Yao Wei-xing. Residual stiffness-residual strength coupled model of composite laminates[J]. Acta Materiae Composites Sinica, 2008, 25(5): 151-156.
20	Ma Y, Xiang Y, Wang L, et al. Fatigue life prediction for aging RC beams considering corrosive environments[J]. Engineering Structures, 2014(79): 211-221.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

材料种类	立方体抗压强度/MPa	棱柱体抗压强度/MPa	屈服强度/MPa	弹性模量/10⁴ MPa
C30混凝土	36.8	26.2	-	3.20
32 mmHRB400	-	-	485	20.5
28 mmHRB400	-	-	467	20.5
HPB300	-	-	347	21.0

试验梁编号	基频f/Hz		误差/%
试验梁编号	试验值	理论计算值	误差/%
TLJ	15.01	15.23	1.44
TLD-1	15.13	15.23	0.66
TLD-2	14.96	15.23	2.43

[1]	安然,王有志. 剪力钉连接件拉剪共同作用抗剪性能[J]. 吉林大学学报(工学版), 2023, 53(9): 2554-2562.
[2]	王峰,刘双瑞,王佳盈,宋佳玲,王俊,张久鹏,黄晓明. 尺寸和形状效应对多孔结构风阻系数的影响[J]. 吉林大学学报(工学版), 2023, 53(6): 1677-1685.
[3]	王俊,李加武,王峰,张久鹏,黄晓明. 简化U形峡谷风速分布及其对悬索桥抖振响应的影响[J]. 吉林大学学报(工学版), 2023, 53(6): 1658-1668.
[4]	王华,王龙林,张子墨,何昕. 基于裂缝宽度变化的连续刚构桥安全性预警技术[J]. 吉林大学学报(工学版), 2023, 53(6): 1650-1657.
[5]	冯宇,郝键铭,王峰,张久鹏,黄晓明. 非平稳极端风作用下大跨桥梁瞬态风致效应分析[J]. 吉林大学学报(工学版), 2023, 53(6): 1638-1649.
[6]	顾正伟,张攀,吕东冶,吴春利,杨忠,谭国金,黄晓明. 基于数值仿真的简支梁桥震致残余位移分析[J]. 吉林大学学报(工学版), 2023, 53(6): 1711-1718.
[7]	吴春利,黄诗茗,李魁,顾正伟,黄晓明,张炳涛,杨润超. 基于数值仿真和统计分析的洪水作用下桥墩作用效应分析[J]. 吉林大学学报(工学版), 2023, 53(6): 1612-1620.
[8]	谭国金,孔庆雯,何昕,张攀,杨润超,朝阳军,杨忠. 基于动力特性和改进粒子群优化算法的桥梁冲刷深度识别[J]. 吉林大学学报(工学版), 2023, 53(6): 1592-1600.
[9]	江辉,李新,白晓宇. 桥梁抗震结构体系发展述评：从延性到韧性[J]. 吉林大学学报(工学版), 2023, 53(6): 1550-1565.
[10]	袁野. 温度和车辆作用下梁式桥梁结构固有频率分析方法[J]. 吉林大学学报(工学版), 2023, 53(6): 1702-1710.
[11]	刘子玉,陈士通,支墨墨,黄晓明,陈哲心. 可“临-永”转换抢修钢墩应急使用极限承载力[J]. 吉林大学学报(工学版), 2023, 53(6): 1601-1611.
[12]	张玥,刘传森,宋飞. 桥台背墙对连续梁桥地震易损性的影响[J]. 吉林大学学报(工学版), 2023, 53(5): 1372-1380.
[13]	兰树伟,周东华,陈旭,莫南明. 双柱式高墩桥梁整体稳定性的实用算法[J]. 吉林大学学报(工学版), 2023, 53(4): 1105-1111.
[14]	孙琪凯,张楠,刘潇,周子骥. 基于Timoshenko梁理论的钢-混组合梁动力折减系数[J]. 吉林大学学报(工学版), 2023, 53(2): 488-495.
[15]	回丽,陆家琛,周松,安金岚,周冠妍,刘小鹏. 热处理对TC4钛合金激光双束焊接接头疲劳性能的影响[J]. 吉林大学学报(工学版), 2023, 53(1): 105-110.