吉林大学学报(工学版) ›› 2024, Vol. 54 ›› Issue (2): 436-444.doi: 10.13229/j.cnki.jdxbgxb.20220400

• 交通运输工程·土木工程 • 上一篇    

基于车轮-桥面相干激励的大跨连续梁桥振动响应

韩智强1(),谢刚2(),卓亚娟1,骆佐龙3,李华腾1   

  1. 1.太原科技大学 车辆与交通工程学院，太原 030024
    2.太原科技大学 先进控制与装备智能化山西省重点实验室，太原 030024
    3.山西大学 电力与建筑学院，太原 030024
  • 收稿日期:2022-04-21 出版日期:2024-02-01 发布日期:2024-03-29
  • 通讯作者: 谢刚 E-mail:2013007@tyust.edu.cn;xiegang@tyust.edu.cn
  • 作者简介:韩智强（1987-），男，副教授，博士. 研究方向：桥梁检测与评估.E-mail：2013007@tyust.edu.cn
  • 基金资助:
    国家自然科学基金项目(51978063);山西省青年基金项目(202203021212306);山西省高等学校科技创新项目(2022L302);山西省研究生精品教学案例项目(2023AL30);太原科技大学研究生联合培养示范基地项目(JD2022019);山西省重点研发计划项目(201903D121176);山西省教学改革项目(J20230840)

Vibration response of continuous girder bridge based on wheel⁃deck coherent excitation

Zhi-qiang HAN1(),Gang XIE2(),Ya-juan ZHUO1,Zuo-long LUO3,Hua-teng LI1   

  1. 1.School of Transportation and Logistics，Taiyuan University of Science and Technology，Taiyuan 030024，China
    2.Shanxi Key Laboratory of Advanced Control and Equipment Intelligence，Taiyuan University of Science and Technology，Taiyuan 030024，China
    3.School of Electric Power and Architecture，Shanxi University，Taiyuan 030024，China
  • Received:2022-04-21 Online:2024-02-01 Published:2024-03-29
  • Contact: Gang XIE E-mail:2013007@tyust.edu.cn;xiegang@tyust.edu.cn

RICH HTML

 0   

PDF (PC)

63

摘要：

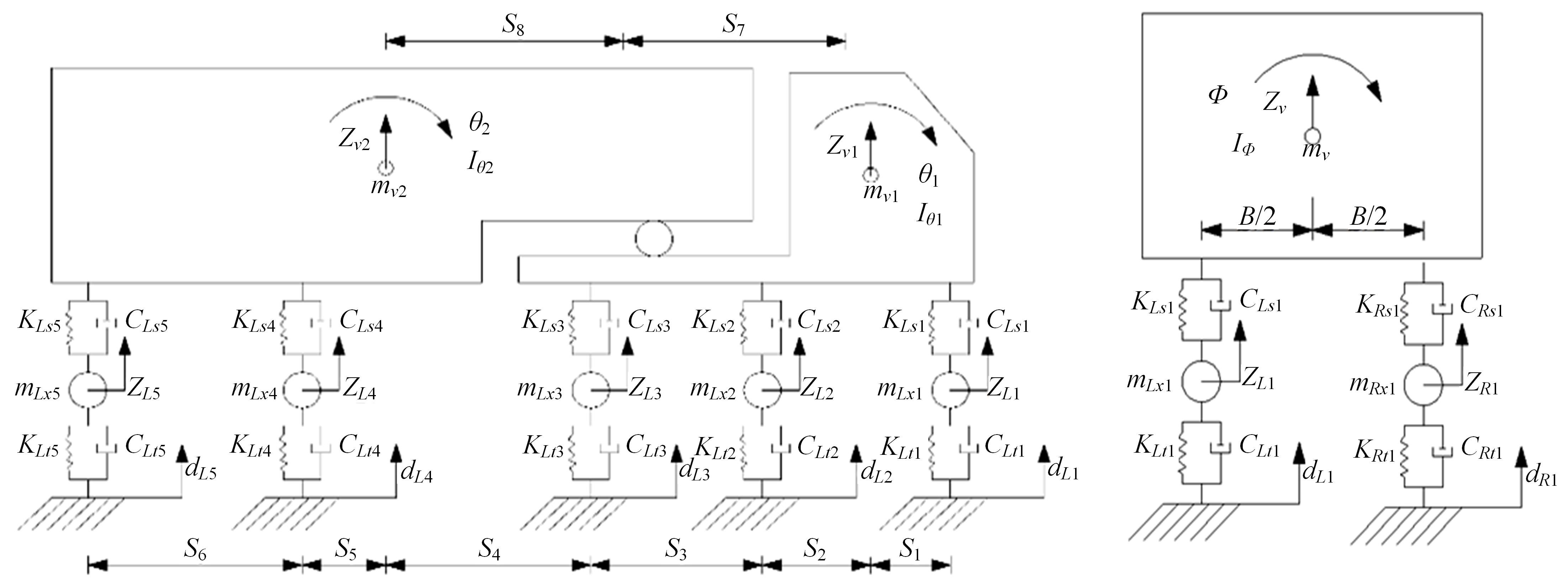
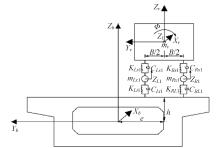
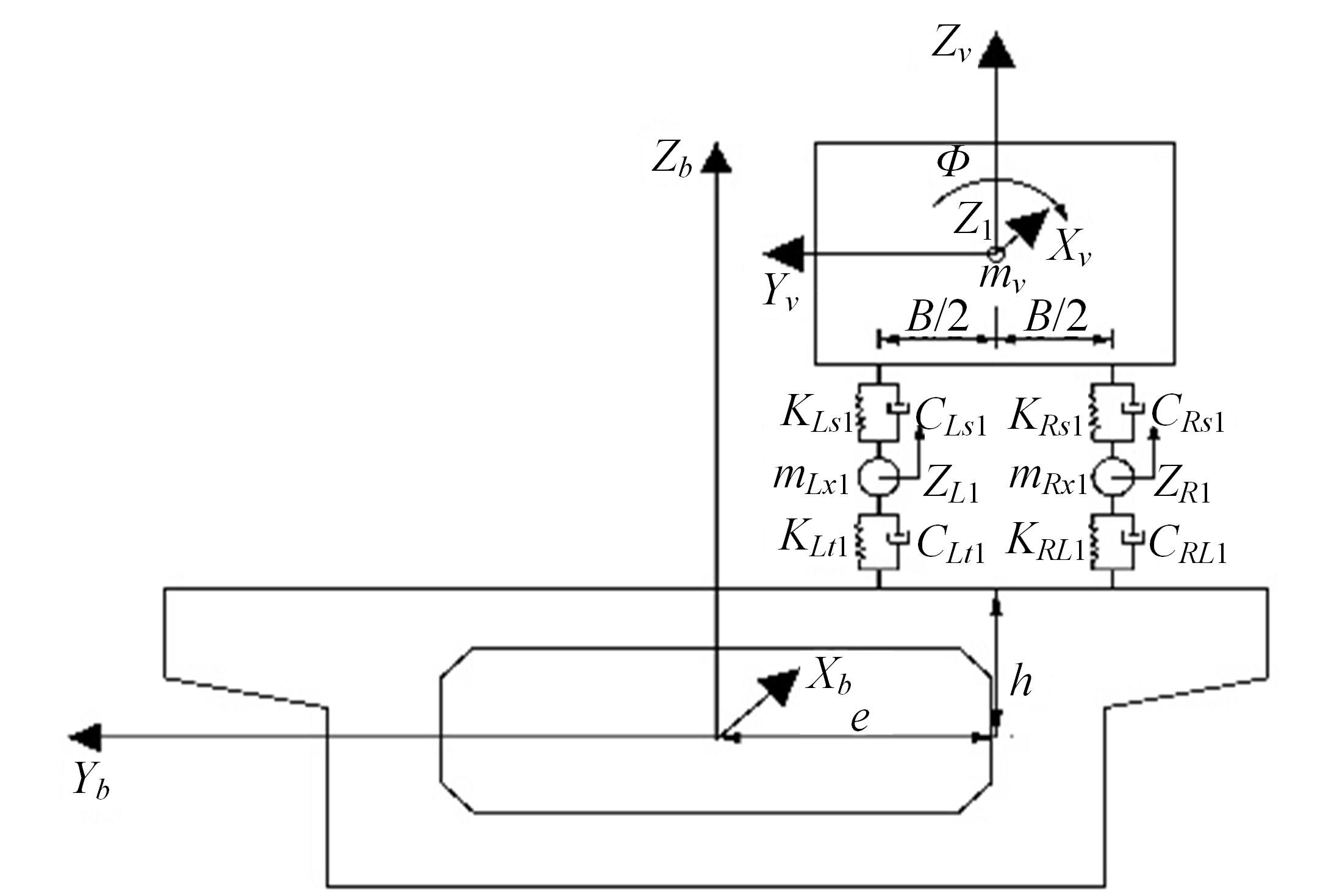
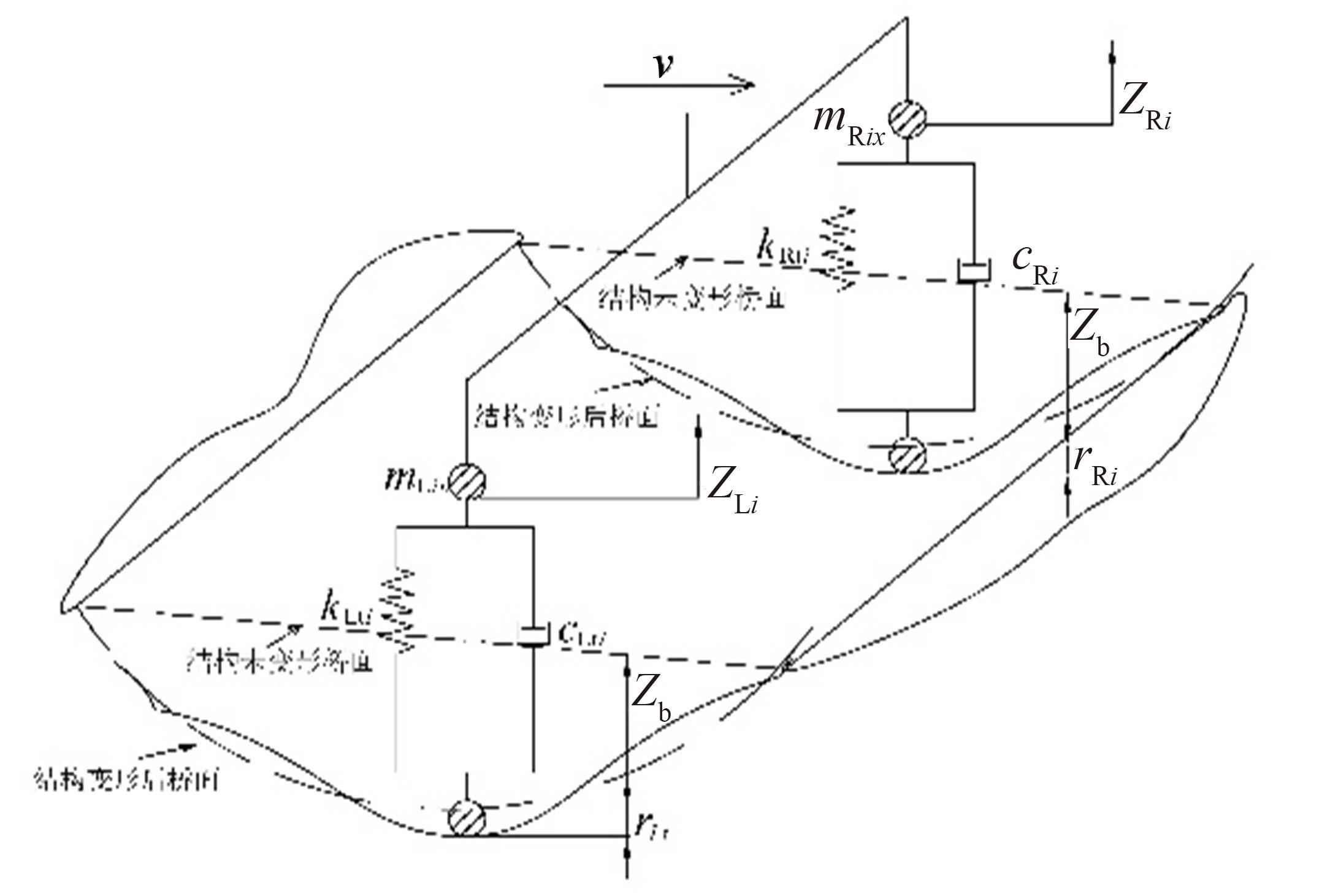
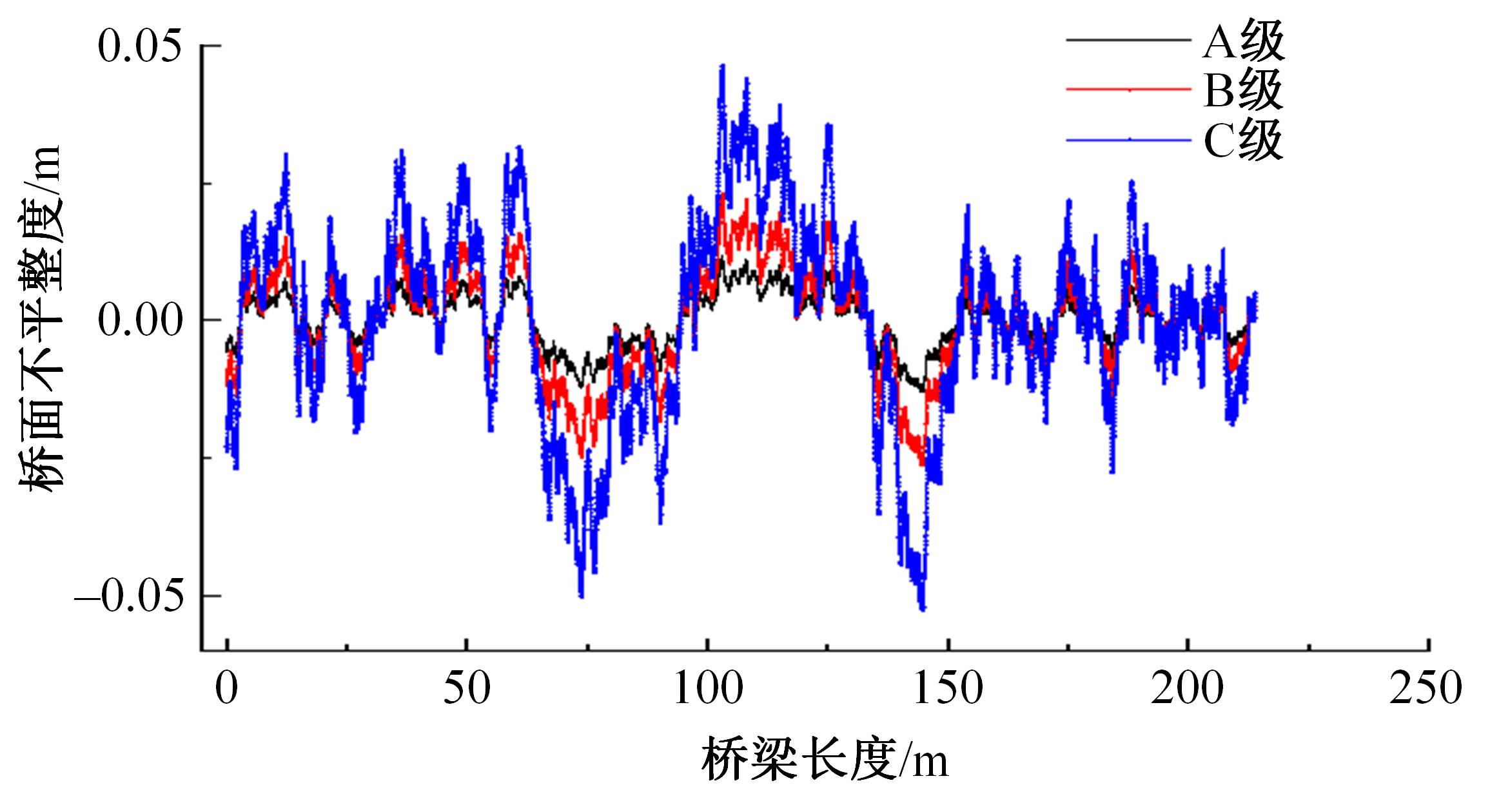
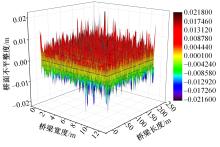
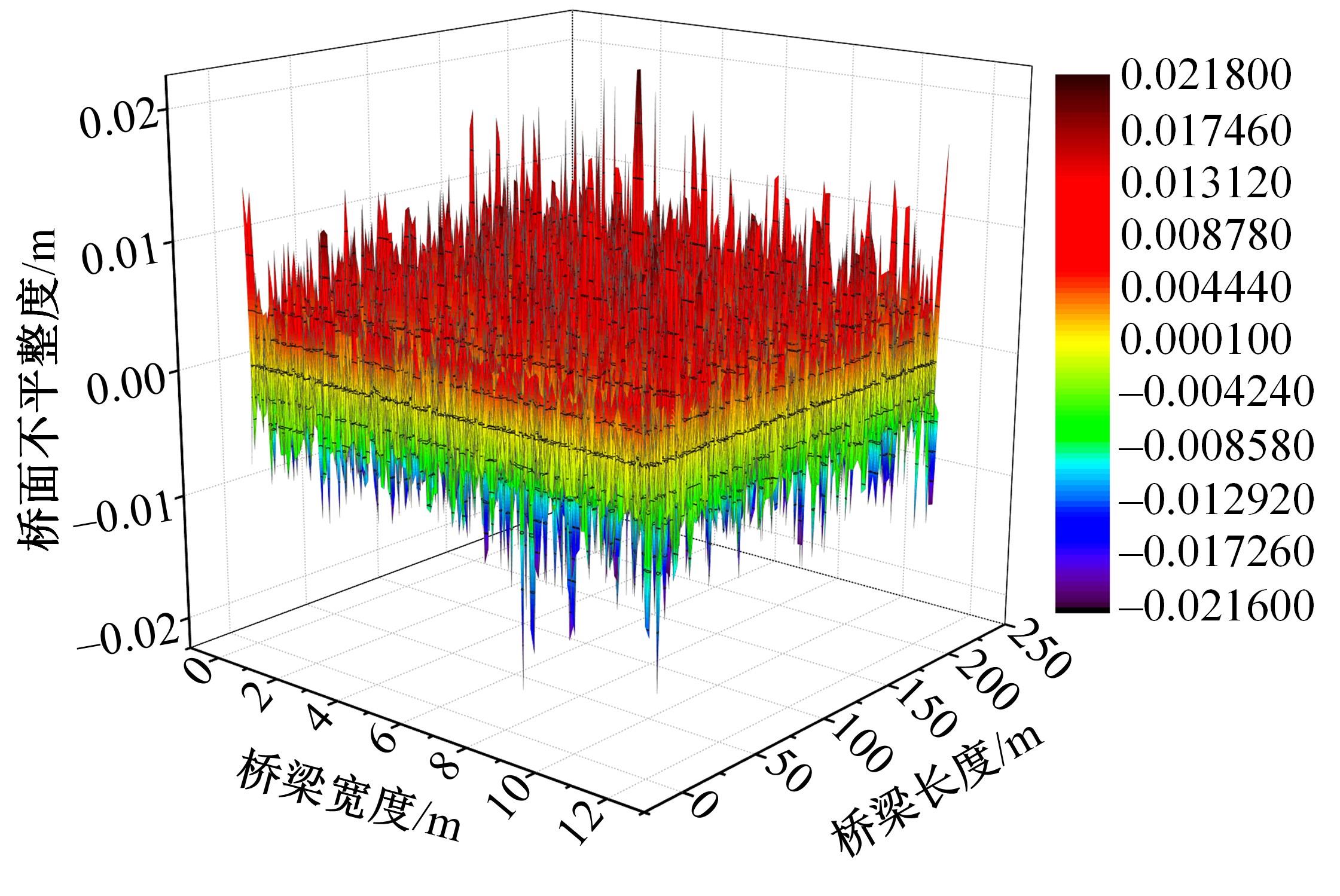
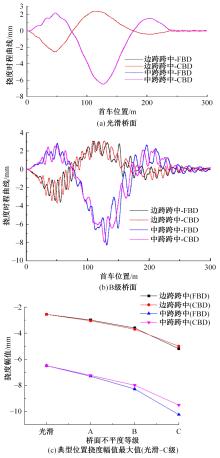
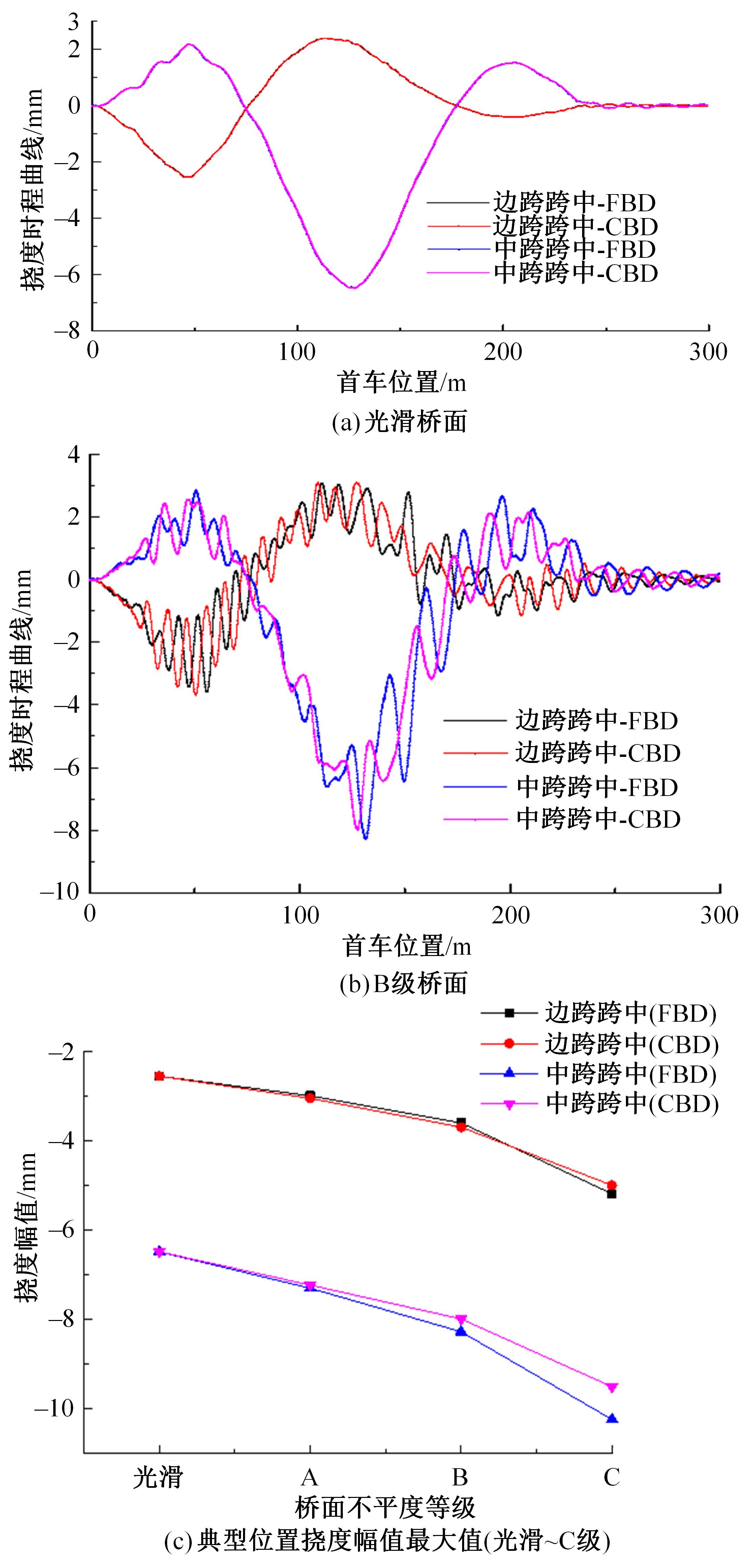
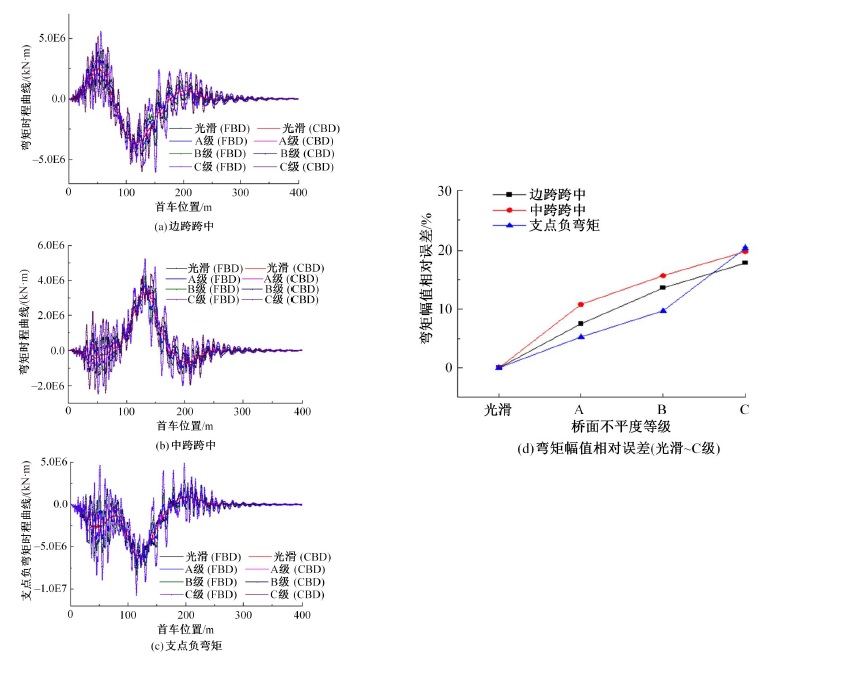
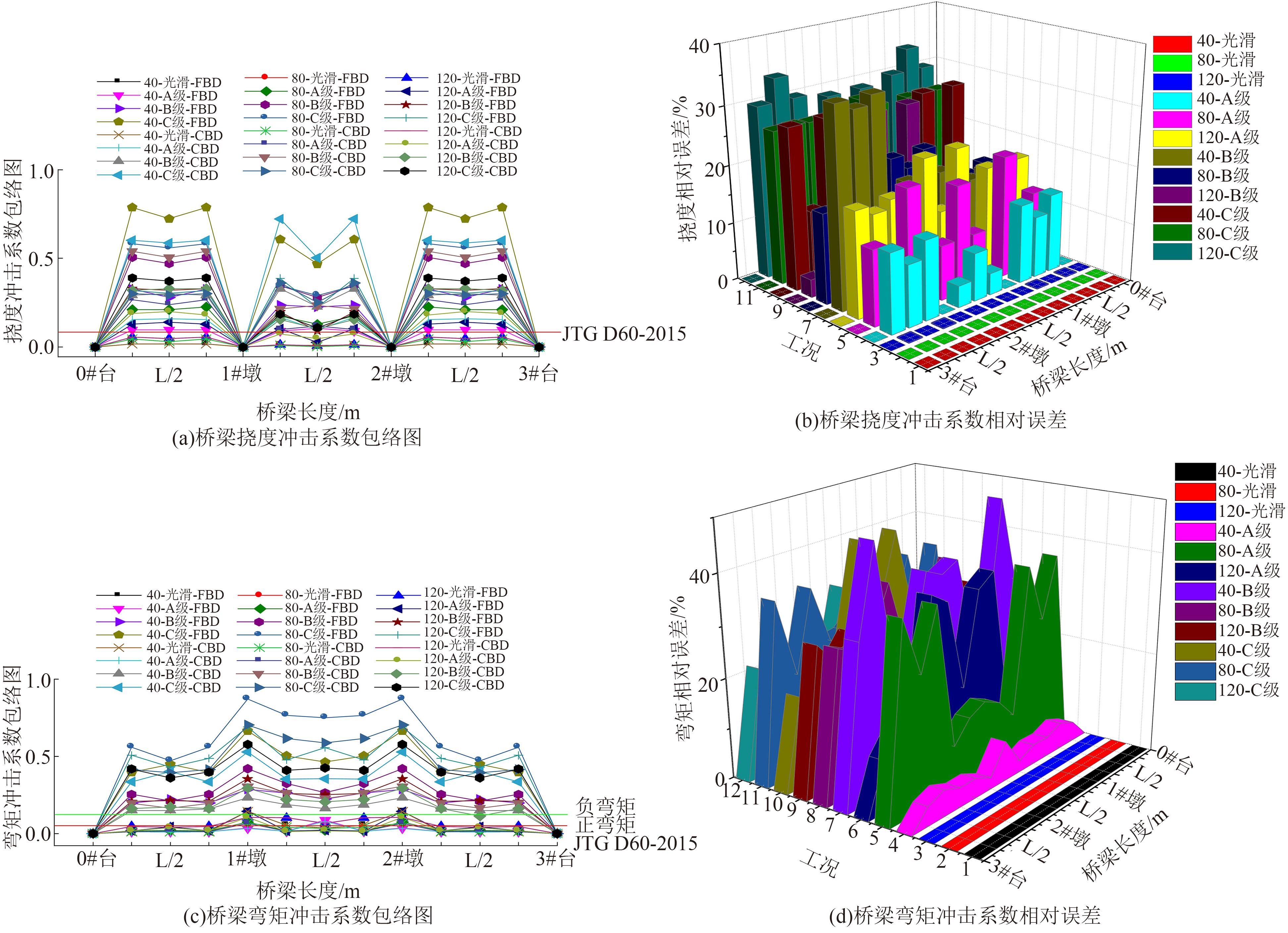
为获取桥面相干激励下大跨连续梁桥动力响应规律，基于虚功原理，建立五轴重载车辆动力学模型，采用模态叠加法建立桥梁动力方程，通过谐波叠加法建立桥面相干激励模型，根据轮-桥间几何和力学耦合关系，组建车轮-桥面相干激励模型，采用Matlab软件编译大跨连续梁桥车桥耦合振动分析系统，并开展不同等级的相干桥面激励模型对大跨连续梁桥动力响应影响研究。结果表明：当未考虑桥面不平顺影响时，桥梁冲击系数均小于规范取值，但随着桥面状况的恶化，结构典型截面的动力响应增长较快，且完全相干模型对桥梁动力响应的影响均大于部分相干激励模型，均超过规范值，其中挠度幅值最大偏差约为7.7%，弯矩幅值最大偏差约为20%，挠度冲击系数相对误差为4%~34%，弯矩冲击系数相对误差为2%~43%；随着车速的增大，桥梁冲击系数呈先增大后减小变化。最后，给出了大跨连续梁桥挠度和弯矩冲击系数包络图。相关研究成果可为连续梁桥的结构动力响应的分析与研究提供参考。

关键词: 桥梁工程, 桥面相干激励模型, 车桥耦合, 动力响应, 冲击系数

Abstract:

To obtain the dynamic response characteristics of long-span continuous beam bridges under coherent excitation of the bridge deck， a comprehensive analysis was conducted based on the principle of virtual work. Firstly， a dynamic model of a five-axle heavy-load vehicle was established. Then， the bridge's dynamic equation was derived using the modal superposition method， a wheel-deck coherent excitation model was established by considering the geometric and mechanical coupling between the wheels and the bridge. The coupled vibration analysis system of the long-span continuous beam bridge was implemented using Matlab software. Subsequently， the impact of different levels of coherent deck excitation models on the dynamic response of the bridge was investigated. The findings revealed that when the influence of bridge deck irregularity was ignored， the impact coefficients of the bridges were smaller than the standard values. However， as the condition of the bridge deck deteriorated， the dynamic response of the representative cross-section of the structure increased significantly. Moreover， it was observed that the completely coherent excitation model had a greater influence on the dynamic response of the bridges compared to the partially coherent excitation model， exceeding the standard values. The maximum deviation of the deflection amplitude was approximately 7.7%， with a maximum deviation of bending moment amplitude of around 20%. The relative errors in deflection impact coefficient ranged from 4% to 34%， while the relative errors in bending moment impact coefficient ranged from 2% to 43%. Additionally， it was noted that the impact coefficient of the bridge initially increased and then decreased with an increase in vehicle speed. Finally， an envelope diagram illustrating the deflection and moment impact coefficients of the long-span continuous beam bridge was provided. These research findings offer valuable insights for the analysis and study of the structural dynamics and response of continuous beam bridges.

Key words: bridge engineering, bridge deck coherent excitation model, vehicle-bridge coupling, dynamic response, impact coefficient

中图分类号: 

  • U442.5

图1

车辆动力学模型示意图"

图2

车轮-桥面几何耦合关系"

图3

车轮-桥面力学耦合关系"

图4

单轮激励空间域模型曲线"

图5

部分相干激励空间域模型样本曲线（A级）"

图6

不同等级桥面不平度下挠度动力响应（v=80 km/h）"

图7

不同等级桥面不平度下弯矩动力响应曲线（v=80 km/h）"

图8

桥梁典型测点布置示意图"

图9

桥梁挠度和弯矩包络图及相对误差"

1 陆兆文, 夏修身, 史军, 等. 设置负刚度装置的大跨长联连续梁桥地震反应分析[J]. 世界地震工程, 2022, 38(2): 181-187.
Lu Zhao-wen, Xia Xiu-shen, Shi Jun, et al. Seismic response analysis of long span continuous girder bridge with negative stiffness device[J]. World Earthquake Engineering, 2022, 38(2):181-187.
2 韩智强, 谢刚, 李路遥, 等. 大跨连续梁桥车桥耦合振动响应[J]. 科学技术与工程, 2022, 22(11): 4588-4595.
Han Zhi-qiang, Xie Gang, Li Lu-yao, et al. Vehicle-Bridge coupling vibration response of long-span continuous girder bridge[J]. Science Technology and Engineering, 2022, 22(11): 4588-4595.
3 冀伟, 邵天彦. 多跨连续梁桥顶推施工双导梁的优化分析[J]. 浙江大学学报: 工学版, 2021, 55(7): 1289-1298.
Ji Wei, Shao Tian-yan. Optimization analysis of double launching noses during launching construction of multi-span continuous girder bridge[J]. Journal of Zhejiang University (Engineering Science), 2021, 55(7): 1289-1298.
4 陈水生, 赵辉, 李锦华, 等. 特重车各轮相干桥面激励对斜拉桥随机振动的影响[J]. 振动工程学报, 2022, 35(2): 318-330.
Chen Shui-sheng, Zhao Hui, Li Jin-hua, et al. Influence of coherent bridge deck excitation from different wheels of an extra-heavy truck on random vibration of a cable-stayed bridge[J]. Journal of Vibration Engineering, 2022, 35(2): 318-330.
5 周勇军, 薛宇欣, 李冉冉, 等. 桥梁冲击系数理论研究和应用进展[J]. 中国公路学报, 2021, 34(4): 31-50.
Zhou Yong-jun, Xue Yu-xin, Li Ran-ran, et al. State-of-the-art of theory and applications of bridge dynamic load allowance[J]. China Journal of Highway and Transport, 2021, 34(4): 31-50.
6 张向东, 杜东宁, 柴源, 等. 基于车-桥耦合振动理论的连续梁桥影响因素分析[J]. 中南大学学报: 自然科学版, 2016, 47(8): 2848-2854.
Zhang Xiang-dong, Du Dong-ning, Chai Yuan, et al. Analysis of influences of different factors on continuous rigid frame bridges based on theory of vehicle-bridge system coupling vibration[J]. Journal of Central South University (Science and Technology), 2016, 47(8): 2848-2854.
7 赵辉, 陈水生, 夏钰桓. 考虑桥面不平顺随机激励的车桥耦合方程精细积分解法[J]. 北京交通大学学报, 2020, 44(4): 65-75.
Zhao Hui, Chen Shui-sheng, Xia Yu-heng. Precise integration method for vehicle-bridge coupling equation considering random excitation of bridge surface irregularity[J]. Journal of Beijing Jiaotong University, 2020, 44(4): 65-75.
8 邓露, 段林利, 何维, 等. 中国公路车-桥耦合振动车辆模型研究[J]. 中国公路学报, 2018, 31(7): 92-100.
Deng Lu, Duan Lin-li, He Wei, et al. Study on vehicle model for vehicle-bridge coupling vibration of highway bridges in China[J]. Chinese Journal of Highways, 2018, 31(7): 92-100.
9 . 公路桥涵设计通用规范 [S].
10 韩智强, 谢刚, 李路遥, 等. 大跨连续梁桥车桥耦合振动响应[J]. 科学技术与工程, 2022, 22(11): 4588-4595.
Han Zhi-qiang, Xie Gang, Li Lu-yao,et al.Vehicle-bridge coupling vibration response of long-span continuous girder bridge[J]. Science Technology and Engineering, 2022, 22(11): 4588-4595.
11 桂水荣, 陈水生, 唐志军. 基于Fourier逆变换法的桥面不平度模拟及测试分析[J]. 公路工程, 2007(6): 39-43.
Gui Shui-rong, Chen Shui-sheng, Tang Zhi-jun. Numerical simulation based on Fourier inverse transform and analyse of road surface roughness on bridge[J]. Highway Engineering, 2007(6): 39-43.
12 韩万水, 马麟, 汪炳, 等. 随机车流-桥梁系统耦合振动精细化分析与动态可视化[J]. 中国公路学报, 2013, 26(4): 78-87.
Han Wan-shui, Ma Lin, Wang Bing, et al. Refinement analysis and dynamic visualization of traffic-bridge coupling vibration system[J]. China Journal of Highway and Transport, 2013, 26(4): 78-87.
13 陈水生, 赵辉, 李锦华, 等. 重车各轮相干桥面激励的桥梁随机振动[J]. 长安大学学报: 自然科学版, 2021, 41(4): 43-55.
Chen Shui-sheng, Zhao Hui, Li Jin-hua, et al. Random vibration of bridge excited by bridge deck irregularity of heavy vehicle with coherent wheels[J]. Journal of Changan University (Natural Science Edition), 2021, 41(4): 43-55.
14 韩智强, 谢刚, 周勇军, 等. 曲线桥梁车桥耦合振动数值分析方法[J]. 吉林大学学报: 工学版, 2023, 53(2): 515-522.
Han Zhi-qiang, Xie Gang, Zhou Yong-jun, et al. Numerical analysis method of vehicle-bridge coupling vibration of curved bridge[J]. Journal of Jilin University(Engineering and Technology Edition), 2023, 53(2): 515-522.
15 Senthilvasan J, Thambiratnam D P, Brameld G H. Dynamic response of a curved bridge under moving truck load[J]. Engineering Structures, 2002, 24: 1283-1293.
16 谭也平, 王健, 刘智超. 基于桥面不平顺导致跳车工况下的车桥相互作用分析[J]. 应用力学学报, 2020, 37(3): 945-952.
Tan Ye-ping, Wang Jian, Liu Zhi-chao. Analysis of vehicle-bridge interaction based on jumping conditions caused by irregular deck[J]. Chinese Journal of Applied Mechanics, 2020, 37(3): 945-952.
17 谭国金, 刘寒冰, 程永春, 等. 基于车-桥耦合振动的简支梁桥冲击效应[J]. 吉林大学学报: 工学版, 2011, 41(1): 62-67.
Tan Guo-jin, Liu Han-bing, Cheng Yong-chun, et al. Analysis of impact of vehicle to simply supported beam bridge based on vehicle-bridge coupled vibration[J]. Journal of Jilin University (Engineering and Technology Edition), 2011, 41(1): 62-67.
18 任宏斌, 陈思忠, 吴志成, 等. 车辆左右车轮路面不平度的时域再现研究[J]. 北京理工大学学报, 2013, 33(3): 257-259.
Ren Hong-bin, Chen Si-zhong, Wu Zhi-cheng, et al. Time domain excitation model of random road profile for left and right wheels[J]. Transactions of Beijing Institute of Technology, 2013, 33(3): 257-259.
19 , 公路桥梁荷载试验规程 [S].
[1] 杨国俊,齐亚辉,石秀名. 基于数字图像技术的桥梁裂缝检测综述[J]. 吉林大学学报(工学版), 2024, 54(2): 313-332.
[2] 谭国金,欧吉,艾永明,杨润超. 基于改进DeepLabv3+模型的桥梁裂缝图像分割方法[J]. 吉林大学学报(工学版), 2024, 54(1): 173-179.
[3] 卫星,高亚杰,康志锐,刘宇辰,赵骏铭,肖林. 低温环境下栓钉环焊缝焊接残余应力场数值模拟[J]. 吉林大学学报(工学版), 2024, 54(1): 198-208.
[4] 龙关旭,张修石,辛公锋,王涛,杨干. 融合机器视觉的桥梁动态称重方法[J]. 吉林大学学报(工学版), 2024, 54(1): 188-197.
[5] 左新黛,张劲泉,赵尚传. 在役混凝土T梁疲劳刚度退化及寿命预测方法[J]. 吉林大学学报(工学版), 2023, 53(9): 2563-2572.
[6] 安然,王有志. 剪力钉连接件拉剪共同作用抗剪性能[J]. 吉林大学学报(工学版), 2023, 53(9): 2554-2562.
[7] 王峰,刘双瑞,王佳盈,宋佳玲,王俊,张久鹏,黄晓明. 尺寸和形状效应对多孔结构风阻系数的影响[J]. 吉林大学学报(工学版), 2023, 53(6): 1677-1685.
[8] 王俊,李加武,王峰,张久鹏,黄晓明. 简化U形峡谷风速分布及其对悬索桥抖振响应的影响[J]. 吉林大学学报(工学版), 2023, 53(6): 1658-1668.
[9] 王华,王龙林,张子墨,何昕. 基于裂缝宽度变化的连续刚构桥安全性预警技术[J]. 吉林大学学报(工学版), 2023, 53(6): 1650-1657.
[10] 冯宇,郝键铭,王峰,张久鹏,黄晓明. 非平稳极端风作用下大跨桥梁瞬态风致效应分析[J]. 吉林大学学报(工学版), 2023, 53(6): 1638-1649.
[11] 顾正伟,张攀,吕东冶,吴春利,杨忠,谭国金,黄晓明. 基于数值仿真的简支梁桥震致残余位移分析[J]. 吉林大学学报(工学版), 2023, 53(6): 1711-1718.
[12] 吴春利,黄诗茗,李魁,顾正伟,黄晓明,张炳涛,杨润超. 基于数值仿真和统计分析的洪水作用下桥墩作用效应分析[J]. 吉林大学学报(工学版), 2023, 53(6): 1612-1620.
[13] 谭国金,孔庆雯,何昕,张攀,杨润超,朝阳军,杨忠. 基于动力特性和改进粒子群优化算法的桥梁冲刷深度识别[J]. 吉林大学学报(工学版), 2023, 53(6): 1592-1600.
[14] 江辉,李新,白晓宇. 桥梁抗震结构体系发展述评：从延性到韧性[J]. 吉林大学学报(工学版), 2023, 53(6): 1550-1565.
[15] 袁野. 温度和车辆作用下梁式桥梁结构固有频率分析方法[J]. 吉林大学学报(工学版), 2023, 53(6): 1702-1710.
Viewed
Full text


Abstract

Cited
  Shared   
  Discussed   
No Suggested Reading articles found!
版权所有 © 《吉林大学学报(工学版)》编辑部
地址：长春市人民大街5988号　电话：+86-431-85095297　传真：+86-431-85094074　E-mail: xbgxb@jlu.edu.cn
本系统由北京玛格泰克科技发展有限公司设计开发