吉林大学学报(工学版) ›› 2023, Vol. 53 ›› Issue (6): 1638-1649.doi: 10.13229/j.cnki.jdxbgxb.20221511

• 交通运输工程·土木工程 • 上一篇    

非平稳极端风作用下大跨桥梁瞬态风致效应分析

冯宇1(),郝键铭1,2(),王峰1,2,张久鹏1,黄晓明3   

  1. 1.长安大学 公路学院，西安 710064
    2.长安大学 风洞实验室，西安 710064
    3.东南大学 交通学院，南京 211189
  • 收稿日期:2022-11-25 出版日期:2023-06-01 发布日期:2023-07-23
  • 通讯作者: 郝键铭 E-mail:Rainingfeng@chd.edu.cn;jianminghao@chd.edu.cn
  • 作者简介:冯宇（1995-），男，博士研究生.研究方向：非平稳风场特性及大跨桥梁抖振.E-mail：Rainingfeng@chd.edu.cn
  • 基金资助:
    国家重点研发计划项目(2021YFB2600600);国家自然科学基金项目(51978077);陕西省自然科学基金项目(2023-JC-QN-0597);重庆市在渝院士牵头创新引导专项项目(2022YSZX-JSX0003CSTB)

Analysis of transient wind⁃induced response of long⁃span bridge under nonstationary wind field

Yu FENG1(),Jian-ming HAO1,2(),Feng WANF1,2,Jiu-peng ZHANG1,Xiao-ming HUANG3   

  1. 1.School of Highway，Chang'an University，Xi'an 710064，China
    2.Wind Tunnel Laboratory，Chang'an University，Xi'an 710064，China
    3.School of Transportation，Southeast University，Nanjing 211189，China
  • Received:2022-11-25 Online:2023-06-01 Published:2023-07-23
  • Contact: Jian-ming HAO E-mail:Rainingfeng@chd.edu.cn;jianminghao@chd.edu.cn

RICH HTML

 2   

PDF (PC)

385

摘要：

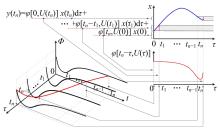
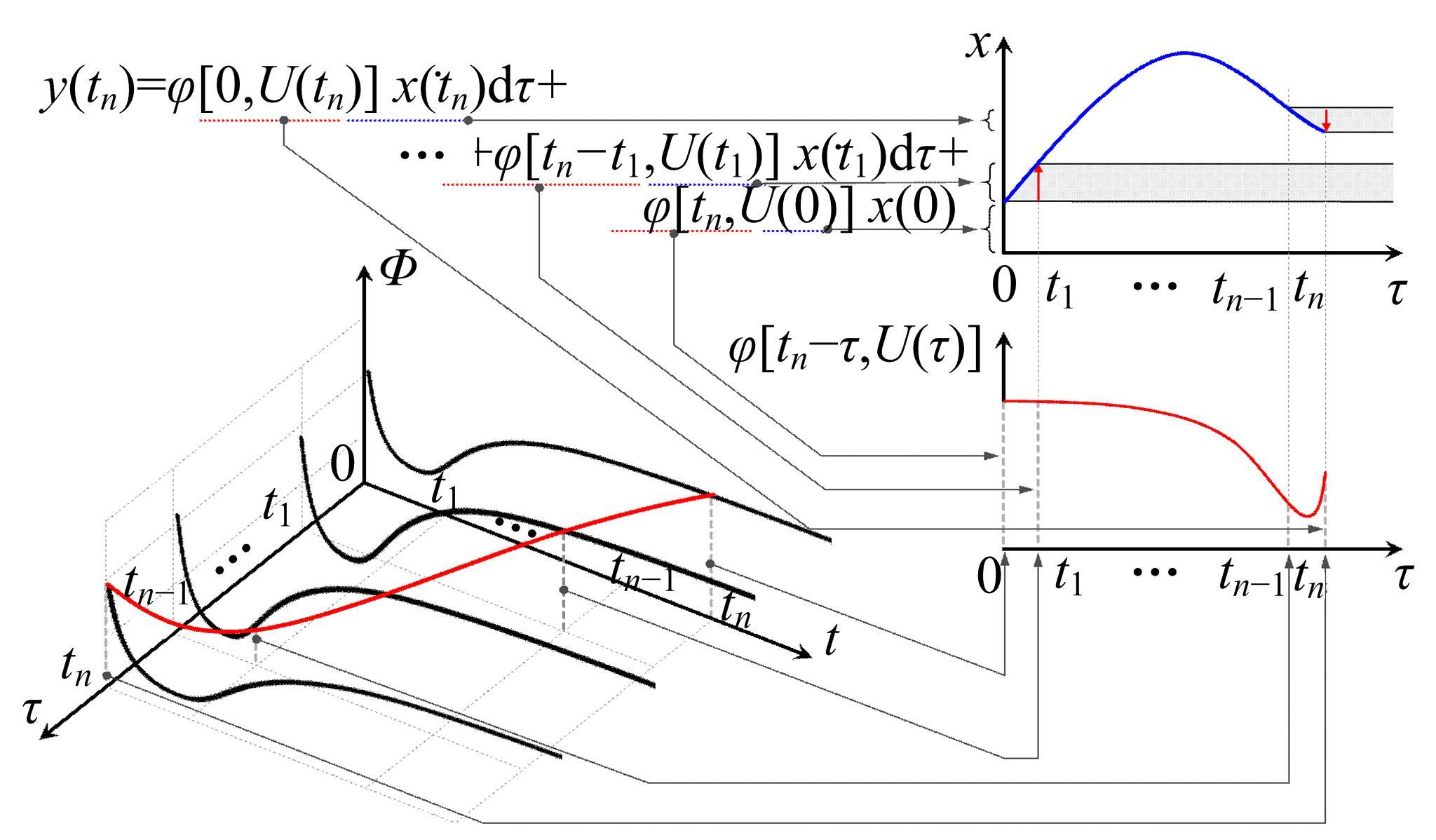
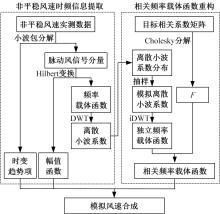
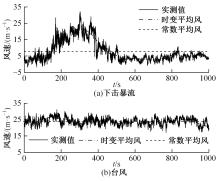
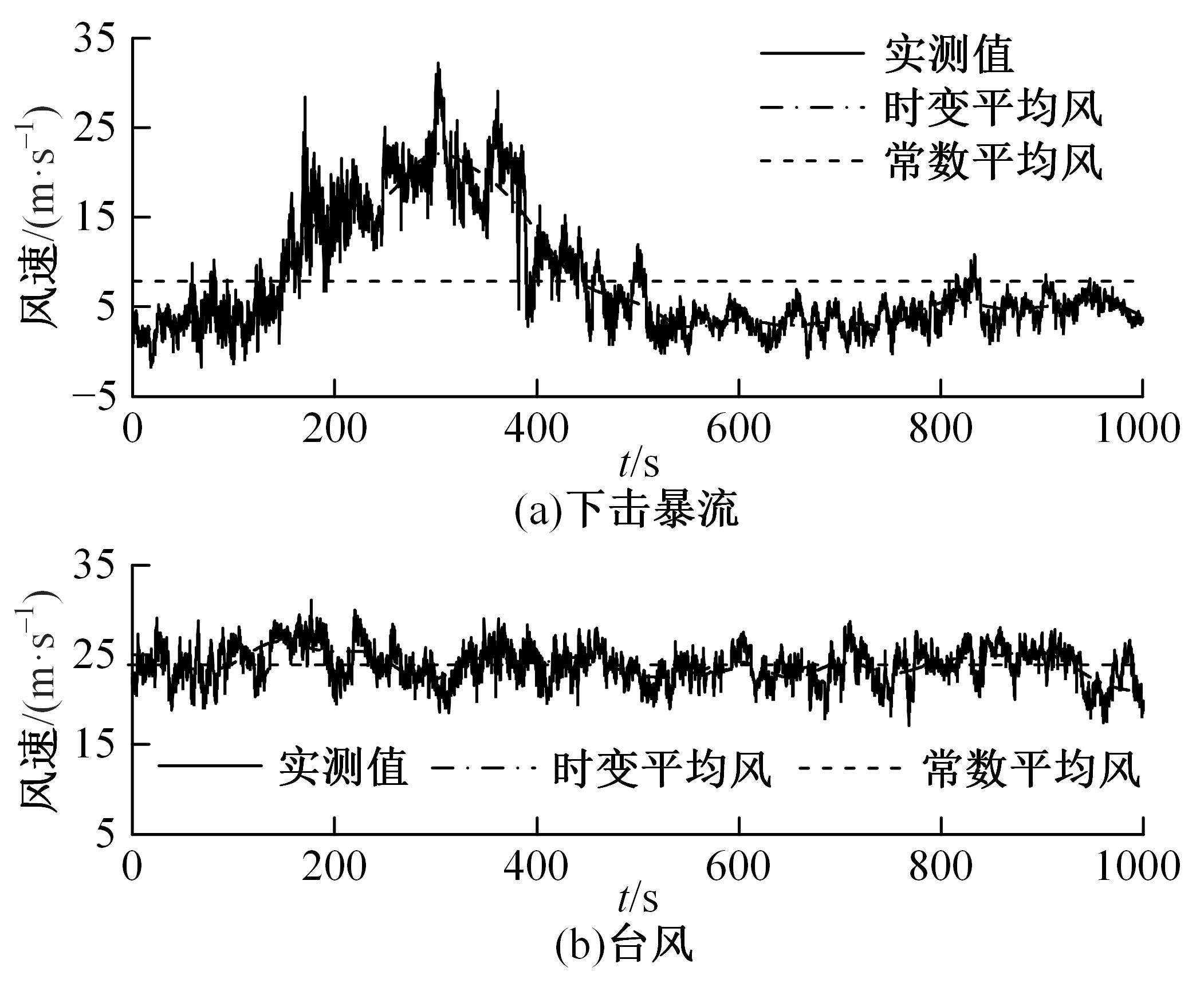
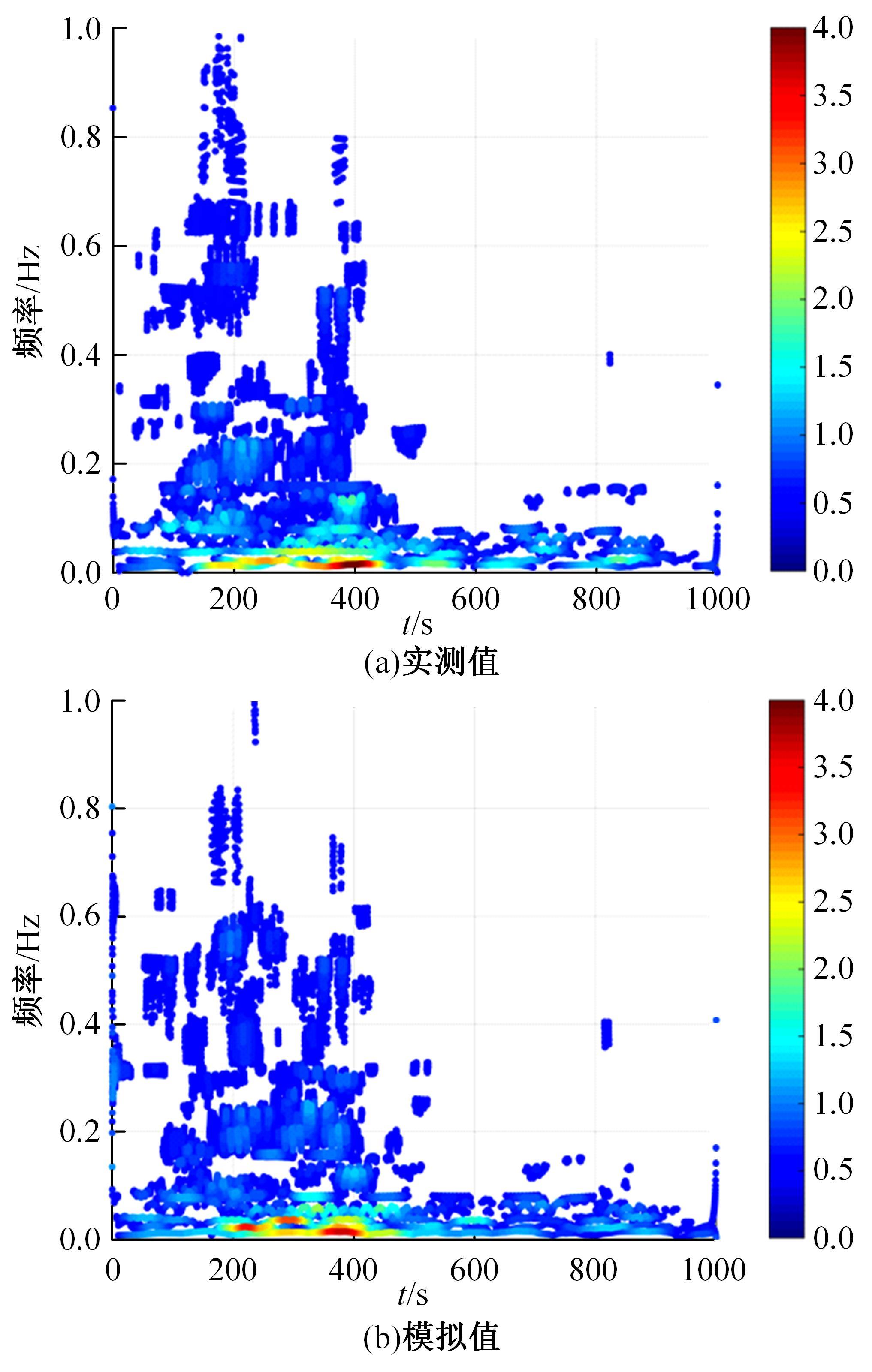
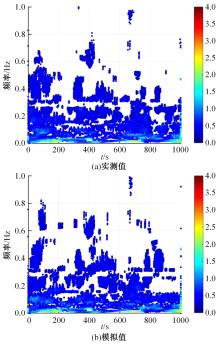
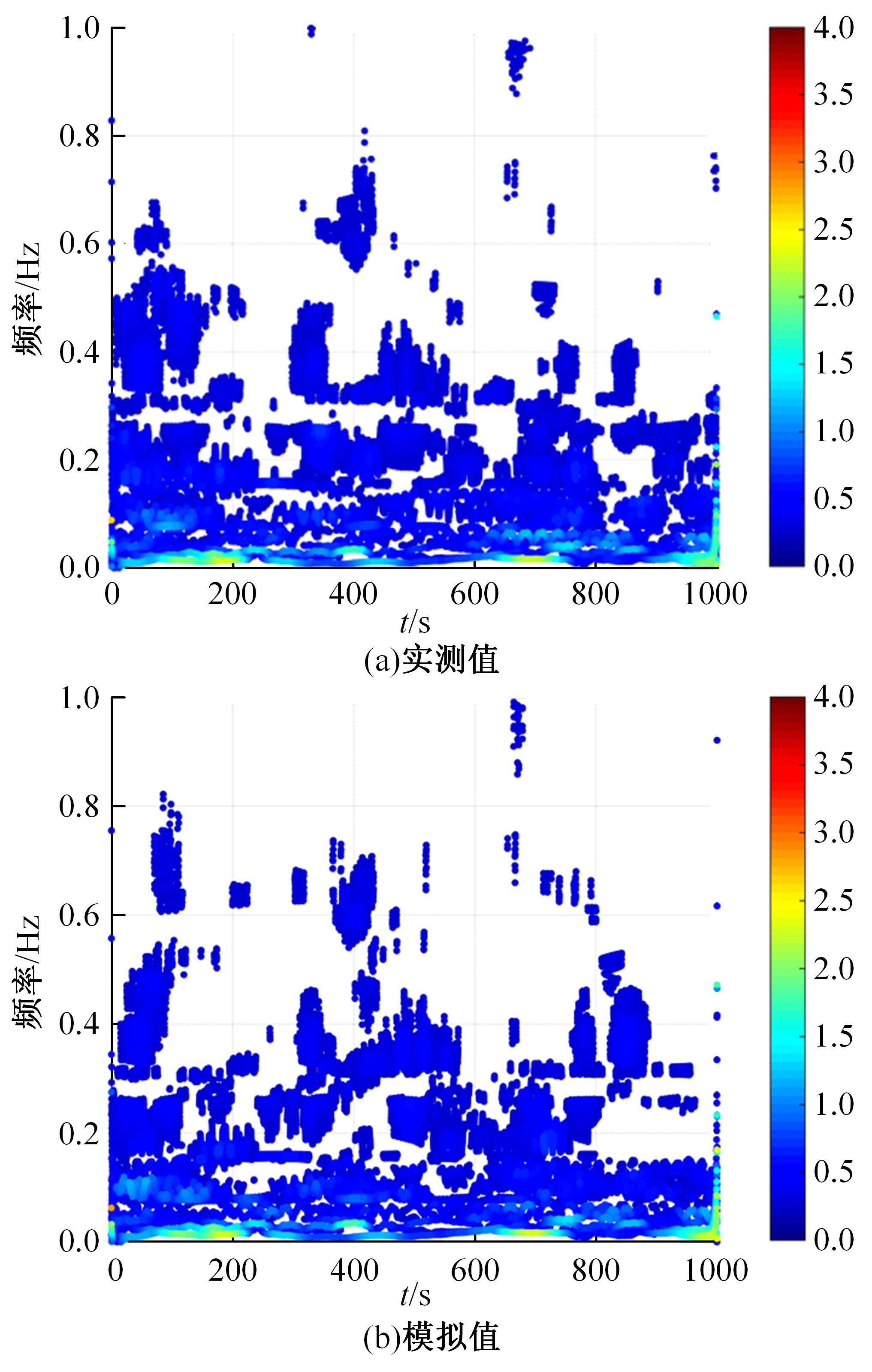
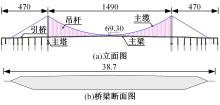
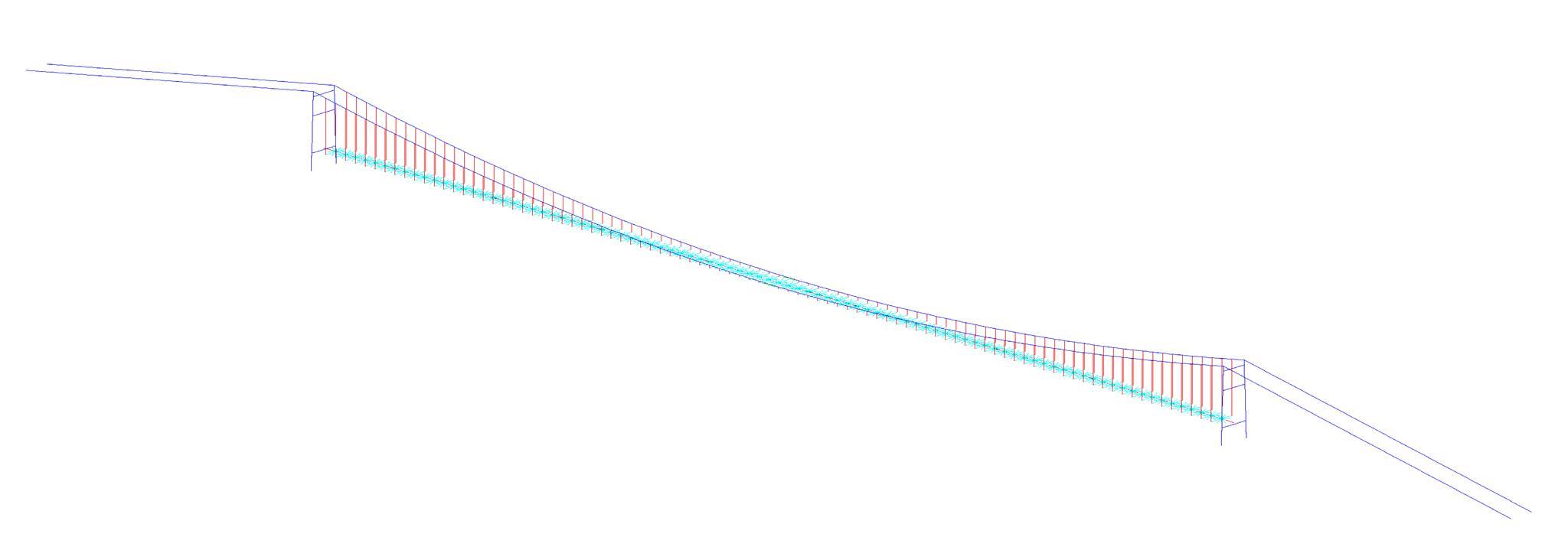
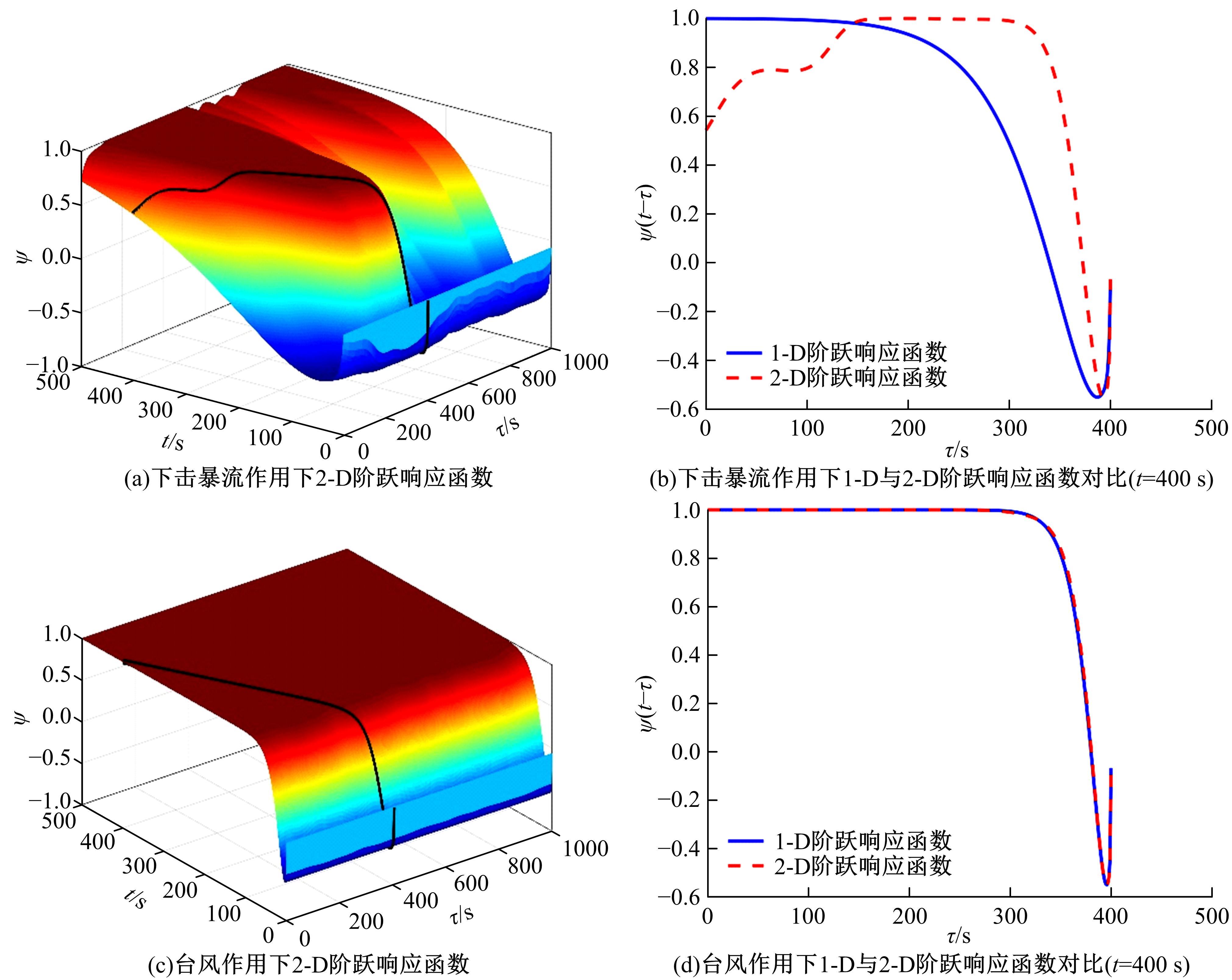
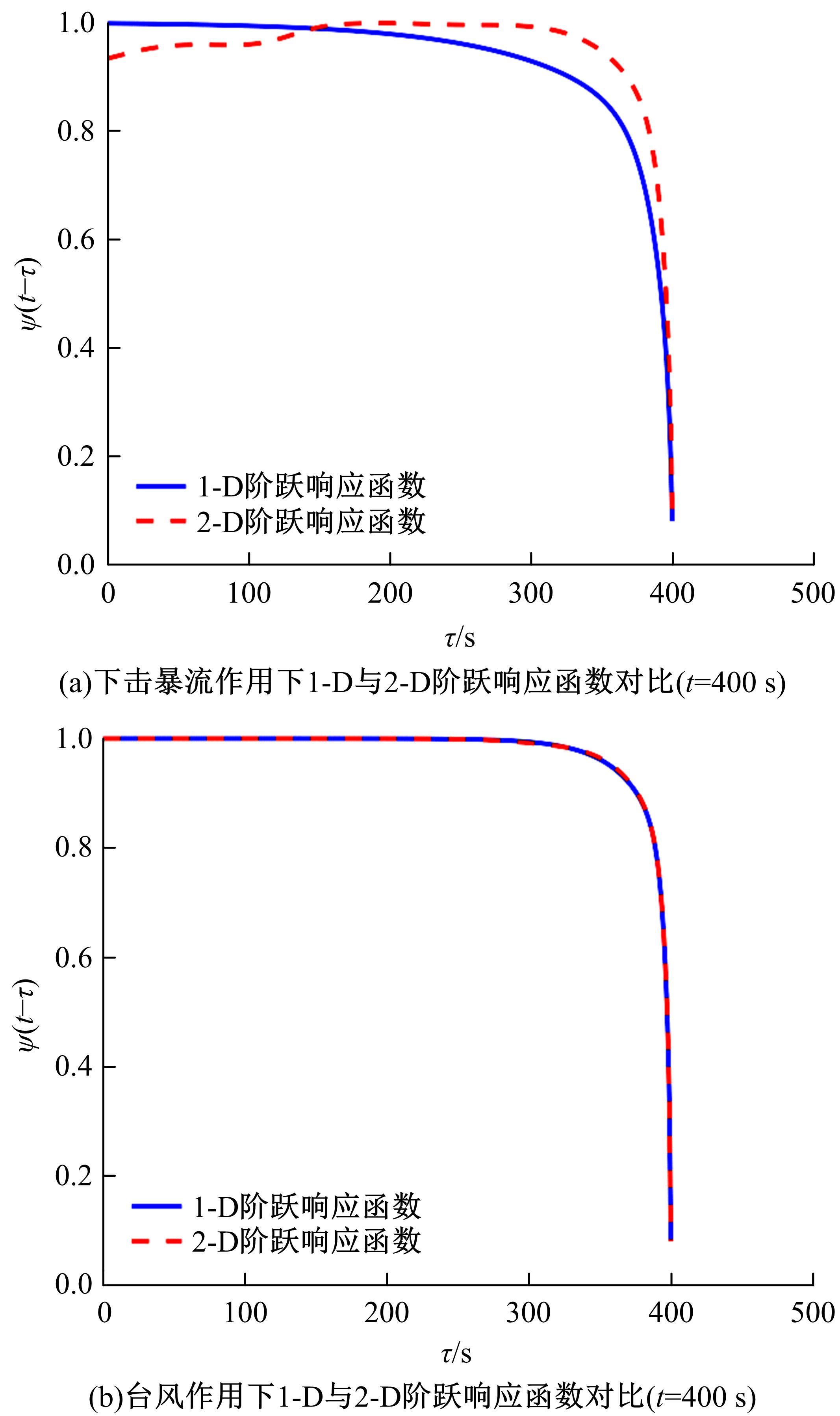
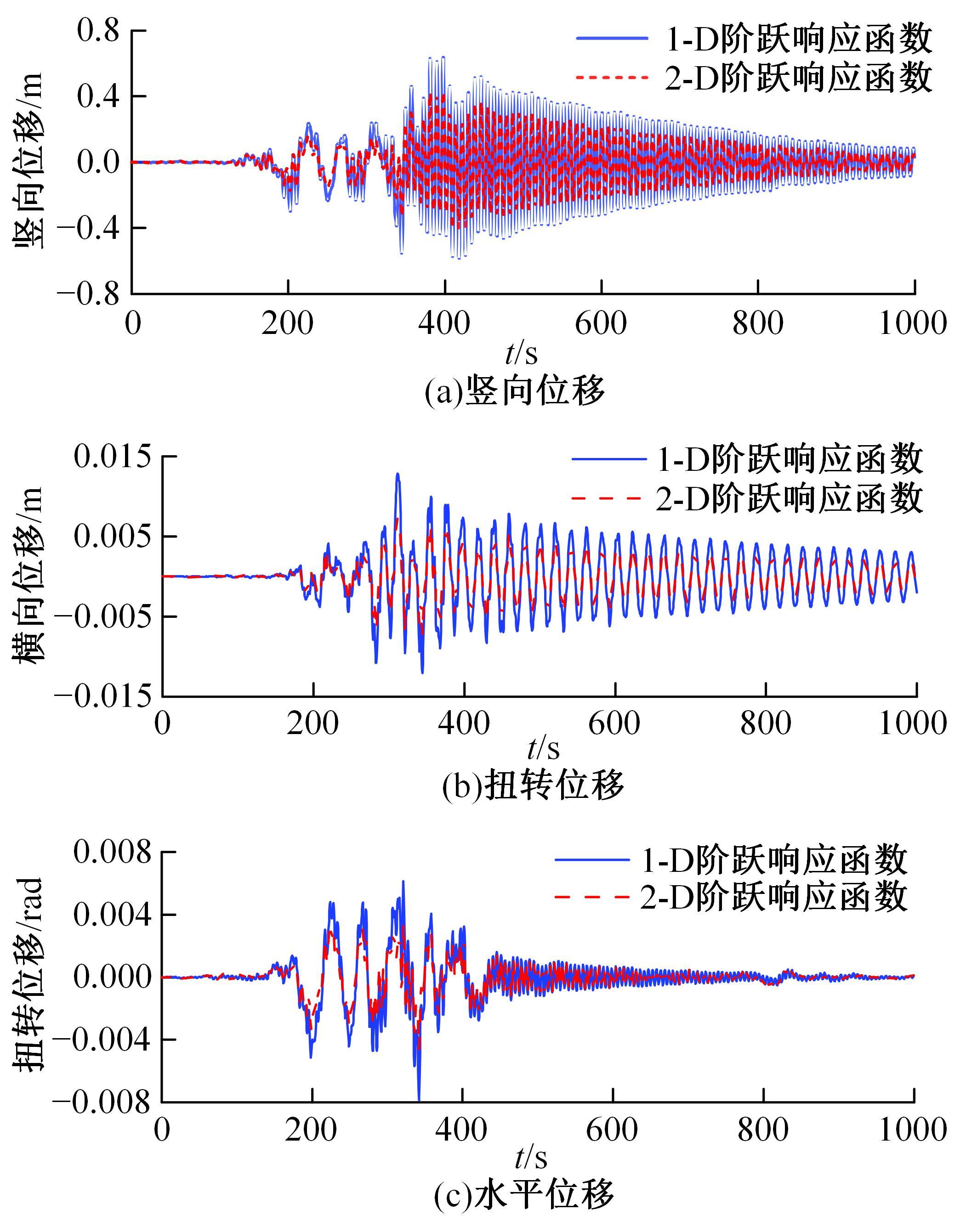
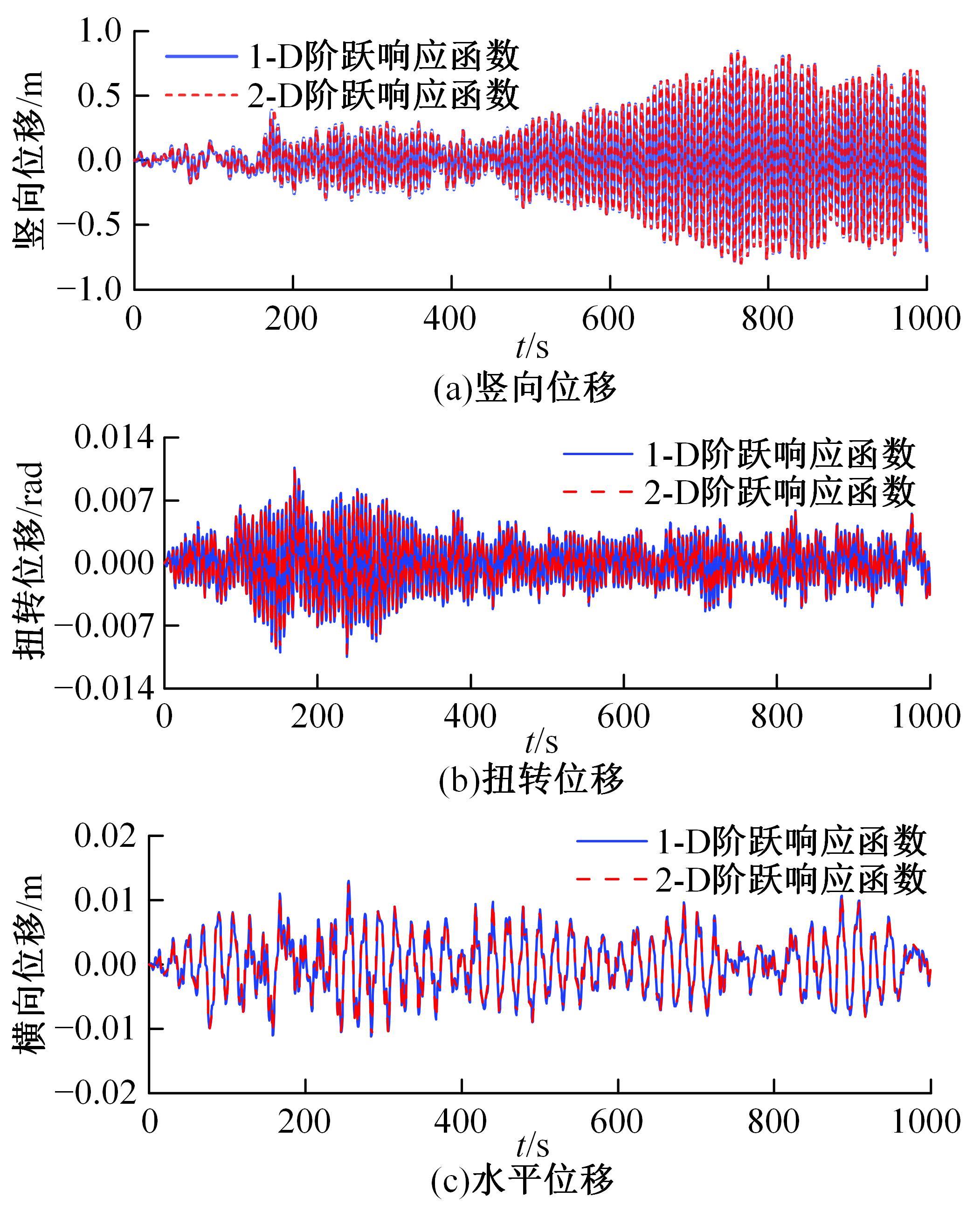
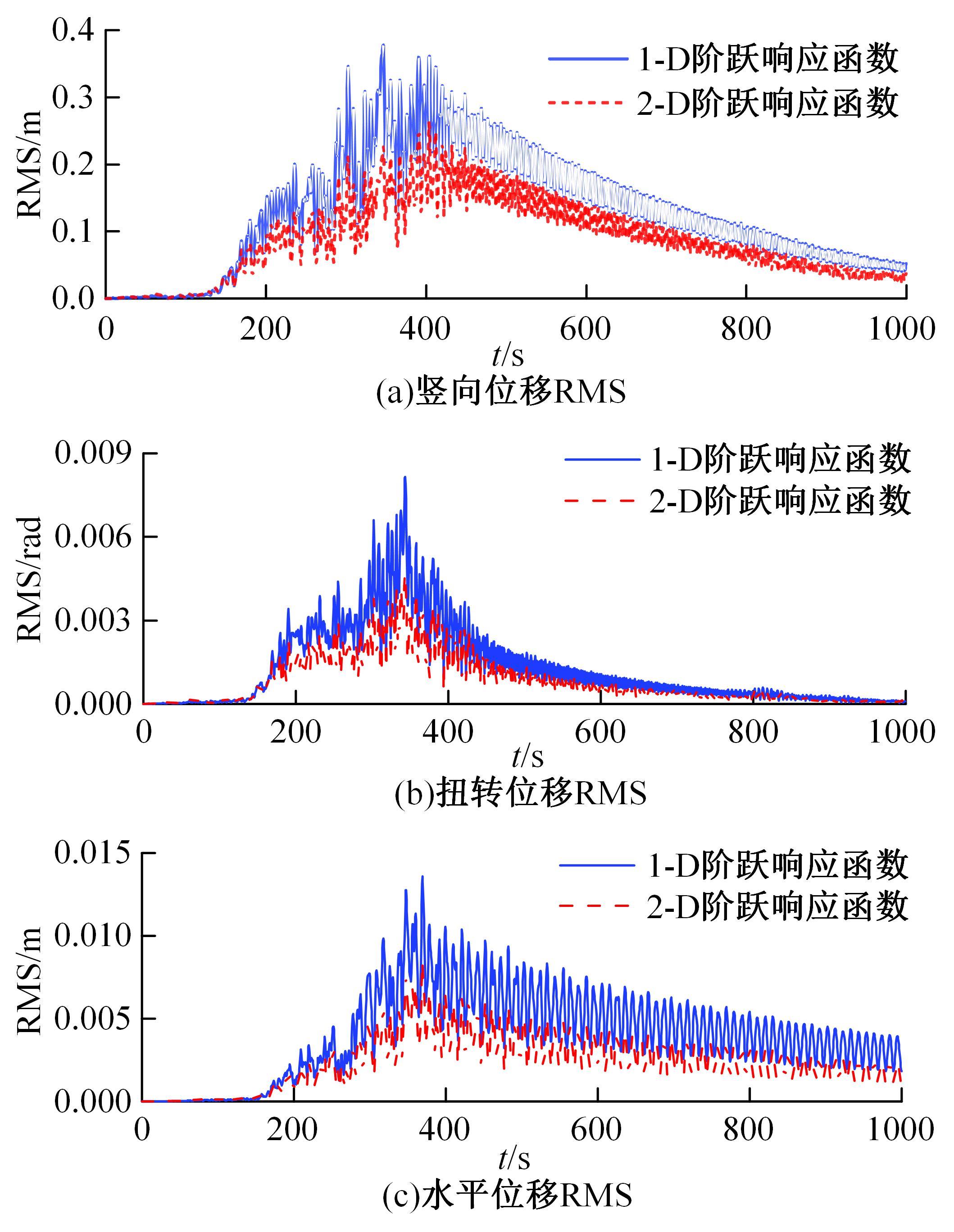
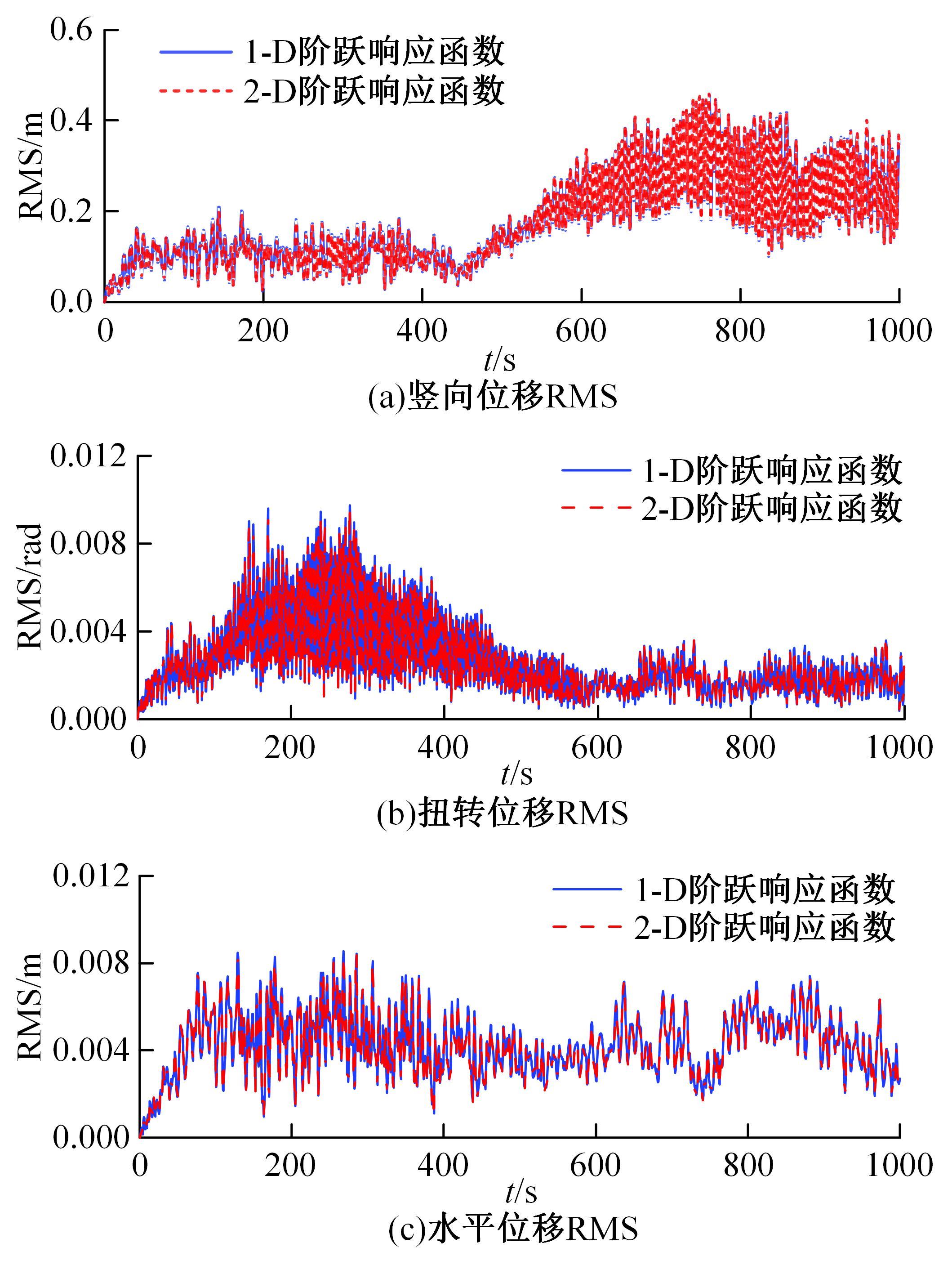
为了研究非平稳风场瞬态效应对风致桥梁响应的影响，基于Hilbert谱进行全桥非平稳风场模拟，采用Cholesky分解嵌入风场空间相性，并引入2-D阶跃响应函数建立了考虑瞬态效应的非平稳风致桥梁抖振响应分析方法。通过下击暴流和台风实测数据提取Hilbert谱，从而高精度地重现真实下击暴流/台风风场。依托某大跨度悬索桥进行非平稳抖振响应分析，探究了非平稳风场瞬态效应对桥梁气动力和抖振响应的影响。研究结果表明：下击暴流风场表现出显著的非平稳特征，时变平均风致瞬态效应明显改变了风-桥耦合系统的气动特征，使阶跃响应函数呈现出显著的时变性，进而影响大跨度桥梁的抖振响应；而在台风风场中，时变平均风致瞬态效应并不显著，对气动力和桥梁抖振响应的影响几乎可以忽略。

关键词: 桥梁工程, 瞬态效应, 非平稳风场, 抖振, 大跨度桥梁

Abstract:

To study the influence of transient effects of nonstationary wind field on wind-induced bridge response， the nonstationary wind field was simulated based on the Hilbert spectrum， and the wind field spatial correlation was introduced by the Cholesky decomposition. The 2-D indicial response function was applied to the nonstationary wind-induced bridge buffeting response analysis method considering the transient effects. The Hilbert spectrum was obtained from the measured data of downburst and typhoon to reappear the real downburst/typhoon wind field with high accuracy. A long-span suspension bridge was selected to implement the nonstationary buffeting response analysis， the influence of transient effects embedded in nonstationary wind field on the aerodynamics and buffeting response of the bridge was discussed. The results show that the downburst presents significant nonstationarity， and the time-varying mean wind-induced transient effects significantly modify the aerodynamics of the wind-bridge interaction system， which exerts a significant impact on the indicial response function and buffeting response of long-span bridges. However， the time-varying mean wind-induced transient effects are insignificant in typhoon case， and the influence on the aerodynamics and the buffeting response is almost negligible.

Key words: bridge engineering, transient effects, nonstationary wind field, buffeting, long-span bridges

中图分类号: 

  • U442

图1

非平稳风速下自激力离散卷积示意图"

图2

基于Hilbert谱的风场模拟流程"

图3

非平稳风速时程和平均风"

图4

模拟脉动风速时程"

图5

下击暴流风速Hilbert谱"

图6

台风风速Hilbert谱"

图7

桥梁示意图（单位：m）"

图8

桥梁有限元模型"

表1

桥梁模态特征"

模态阶次振型特点频率相对误差/%
本文风洞试验本文风洞试验
1一阶正对称横弯一阶正对称横弯0.048 9000.049 411.03
2一阶反对称竖弯一阶反对称竖弯0.087 9100.087 950.05
3一阶反对称横弯一阶反对称横弯0.122 3410.121 740.49
4一阶正对称竖弯一阶正对称竖弯0.125 1180.123 761.10
5二阶正对称竖弯二阶正对称竖弯0.1704010.168 551.10
6二阶反对称竖弯二阶反对称竖弯0.187 9920.185 591.29
7主缆振动主缆振动0.212 4800.207 312.49
8主缆振动主缆振动0.212 6100.215 371.28
9扭转扭转0.217 0200.218 920.87
10主缆振动主缆振动0.220 1800.219 960.10

表2

自激力阶跃响函数参数"

参数a1a2a3b1b2b3
φLh

-3.669

E-01

-1.288E+02

1.302

E+02

3.721

E+00

1.293

E-01

1.271

E-01

φLα

1.280

E+04

7.918

E+00

-1.280E+04

3.218

E-01

5.282

E-01

3.219

E-01

φMh

1.663

E+02

-1.826E-04-1.656E+02

1.142

E-02

1.051

E+00

1.121

E-02

φMα

2.752

E-01

1.348

E+03

-1.348E+03

6.814

E-01

1.691

E-01

1.692

E-01

图9

自激力阶跃响应函数"

图10

抖振力阶跃响应函数"

图11

下击暴流作用下桥梁跨中抖振响应"

图12

台风作用下桥梁跨中抖振响应"

图13

下击暴流作用下桥梁跨中抖振响应RMS"

图14

台风作用下桥梁跨中抖振响应RMS"

1 陶天友, 王浩, 姚程渊. 非平稳风速的 HHS 时频状态表征[J]. 振动工程学报, 2019, 32(1): 49-55.
Tao Tian-you, Wang Hao, Yao Cheng-yuan. HHS-based time-frequency characterization of non-statioanry wind velocities[J]. Journal of Vibration Engineering, 2019, 32(1): 49-55.
2 Hao J, Wu T. Downburst-induced transient response of a long-span bridge: a CFD-CSD-based hybrid approach[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2018, 179: 273-286.
3 Chen L, Letchford C W. Proper orthogonal decomposition of two vertical profiles of full-scale nonstationary downburst wind speeds[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2005, 93(3): 187-216.
4 Xu Y L, Chen J. Characterizing nonstationary wind speed using empirical mode decomposition[J]. Journal of Structural Engineering, 2004, 130(6): 912-920.
5 Huang G, Su Y, Kareem A, et al. Time-frequency analysis of nonstationary process based on multivariate empirical mode decomposition[J]. Journal of Engineering Mechanics, 2016, 142(1): No.04015065.
6 Su Y, Huang G, Xu Y L. Derivation of time-varying mean for non-stationary downburst winds[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2015, 141: 39-48.
7 Priestley M B. Evolutionary spectra and non‐stationary processes[J]. Journal of the Royal Statistical Society: Series B (Methodological), 1965, 27(2): 204-229.
8 Deodatis G. Non-stationary stochastic vector processes: seismic ground motion applications[J]. Probabilistic Engineering Mechanics, 1996, 11(3): 149-167.
9 Huang G. An efficient simulation approach for multivariate nonstationary process: hybrid of wavelet and spectral representation method[J]. Probabilistic Engineering Mechanics, 2014, 37: 74-83.
10 Li Y, Kareem A. Simulation of multivariate nonstationary random processes by FFT[J]. Journal of Engineering Mechanics, 1991, 117(5): 1037-1058.
11 Xu Y L, Hu L, Kareem A. Conditional simulation of nonstationary fluctuating wind speeds for long-span bridges[J]. Journal of Engineering Mechanics, 2014, 140(1): 61-73.
12 Wen Y, Gu P. Description and simulation of nonstationary processes based on Hilbert spectra[J]. Journal of Engineering Mechanics, 2004, 130(8): 942-951.
13 Wang H, Wu T. Hilbert-wavelet-based nonstationary wind field simulation: a multiscale spatial correlation scheme[J]. Journal of Engineering Mechanics, 2018, 144(8): No.04018063.
14 Kareem A. Numerical simulation of wind effects: a probabilistic perspective[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96(10/11): 1472-1497.
15 Cao B, Sarkar P P. Numerical simulation of dynamic response of a long-span bridge to assess its vulnerability to non-synoptic wind[J]. Engineering Structures, 2015, 84: 67-75.
16 Butler K, Cao S, Kareem A, et al. Surface pressure and wind load characteristics on prisms immersed in a simulated transient gust front flow field[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2010, 98(6/7): 299-316.
17 Shirato H, Maeta K, Kato Y, et al. Transient drag force on 2-D bluff bodies under gusty wind condition[C]∥7th Asia-Pacific Conference on Wind Engineering, Taipei, China, 2009: 1-8.
18 Hu L, Xu Y L, Huang W F. Typhoon-induced non-stationary buffeting response of long-span bridges in complex terrain[J]. Engineering Structures, 2013, 57: 406-415.
19 Chen X. Analysis of multimode coupled buffeting response of long-span bridges to nonstationary winds with force parameters from stationary wind[J]. Journal of Structural Engineering, 2015, 141(4): No.04014131.
20 Hao J, Wu T. Nonsynoptic wind-induced transient effects on linear bridge aerodynamics[J]. Journal of Engineering Mechanics, 2017, 143(9): No. 04017092.
21 陶天友, 王浩. 大跨度桥梁主梁节段模型非平稳抖振时域模拟与分析[J]. 振动工程学报, 2019, 32(5): 830-836.
Tao Tian-you, Wang Hao. Time-domain simulation and analysis of nonstationary buffeting responses of girder section model of a long-span bridge[J]. Journal of Vibration Engineering, 2019, 32(5): 830-836.
22 Wu T, Kareem A. Revisiting convolution scheme in bridge aerodynamics: comparison of step and impulse response functions[J]. Journal of Engineering Mechanics, 2014, 140(5): No.04014008.
23 Scanlan R H, Béliveau J G, Budlong K S. Indicial aerodynamic functions for bridge decks[J]. Journal of the Engineering Mechanics Division, 1974, 100(4): 657-672.
24 Gabor D. Theory of communication. Part 1: the analysis of information[J]. Journal of the Institution of Electrical Engineers-part III: Radio and Communication Engineering, 1946, 93(26): 429-441.
25 Boashash B. Estimating and interpreting the instantaneous frequency of a signal. I. Fundamentals[J]. Proceedings of the IEEE, 1992, 80(4): 520-538.
26 Olhede S, Walden A. The Hilbert spectrum via wavelet projections[J]. Proceedings of the Royal Society of London Series A: Mathematical, Physical and Engineering Sciences, 2004, 460(2044): 955-975.
27 Wang L, Mccullough M, Kareem A. A data-driven approach for simulation of full-scale downburst wind speeds[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2013, 123: 171-190.
28 Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London Series A: Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903-995.
29 Wu T. Simulation of nonstationary wind velocity field utilizing multi-scale spatial correlation nested Hilbert-wavelet scheme[C]∥14th International Conference on Wind Engineering, Porto Alegre, Brazil, 2015: 1-16.
30 Zhang S, Solari G, De Gaetano P, et al. A refined analysis of thunderstorm outflow characteristics relevant to the wind loading of structures[J]. Probabilistic Engineering Mechanics, 2018, 54: 9-24.
31 Song L, Chen W, Wang B, et al. Characteristics of wind profiles in the landfalling typhoon boundary layer[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2016, 149: 77-88.
32 Chen L, Letchford C. Numerical simulation of extreme winds from thunderstorm downbursts[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2007, 95(9-11): 977-990.
33 陈艾荣. 润扬长江公路大桥悬索桥抗风性能试验研究[R]. 上海:同济大学土木工程防灾国家重点实验室,2001.
34 Jones R T. The unsteady lift of a wing of finite aspect ratio[R]. Washington DC: National Advisory Committee for Aeronautics, 1940.
[1] 吴春利,黄诗茗,李魁,顾正伟,黄晓明,张炳涛,杨润超. 基于数值仿真和统计分析的洪水作用下桥墩作用效应分析[J]. 吉林大学学报(工学版), 2023, 53(6): 1612-1620.
[2] 谭国金,孔庆雯,何昕,张攀,杨润超,朝阳军,杨忠. 基于动力特性和改进粒子群优化算法的桥梁冲刷深度识别[J]. 吉林大学学报(工学版), 2023, 53(6): 1592-1600.
[3] 江辉,李新,白晓宇. 桥梁抗震结构体系发展述评：从延性到韧性[J]. 吉林大学学报(工学版), 2023, 53(6): 1550-1565.
[4] 刘子玉,陈士通,支墨墨,黄晓明,陈哲心. 可“临-永”转换抢修钢墩应急使用极限承载力[J]. 吉林大学学报(工学版), 2023, 53(6): 1601-1611.
[5] 张玥,刘传森,宋飞. 桥台背墙对连续梁桥地震易损性的影响[J]. 吉林大学学报(工学版), 2023, 53(5): 1372-1380.
[6] 兰树伟,周东华,陈旭,莫南明. 双柱式高墩桥梁整体稳定性的实用算法[J]. 吉林大学学报(工学版), 2023, 53(4): 1105-1111.
[7] 孙琪凯,张楠,刘潇,周子骥. 基于Timoshenko梁理论的钢-混组合梁动力折减系数[J]. 吉林大学学报(工学版), 2023, 53(2): 488-495.
[8] 叶华文,段智超,刘吉林,周渝,韩冰. 正交异性钢⁃混组合桥面的轮载扩散效应[J]. 吉林大学学报(工学版), 2022, 52(8): 1808-1816.
[9] 王立峰,肖子旺,于赛赛. 基于Bayesian网络的多塔斜拉桥挂篮系统风险分析的新方法[J]. 吉林大学学报(工学版), 2022, 52(4): 865-873.
[10] 张彦玲,王灿,张旭,王昂洋,李运生. 不同吊杆形式悬索桥人致振动分析及舒适度评价[J]. 吉林大学学报(工学版), 2022, 52(11): 2644-2652.
[11] 钟昌均,王忠彬,柳晨阳. 悬索桥主索鞍承载力影响因素及结构优化[J]. 吉林大学学报(工学版), 2021, 51(6): 2068-2078.
[12] 陈巍,万田保,王忠彬,厉萱,沈锐利. 悬索桥主缆除湿的内部送气管道设计与性能[J]. 吉林大学学报(工学版), 2021, 51(5): 1749-1755.
[13] 郭殊伦,钟铁毅,闫志刚. 大跨度斜拉桥拉索的抖振响应计算方法[J]. 吉林大学学报(工学版), 2021, 51(5): 1756-1762.
[14] 高凯,刘纲. 全局临界强度分枝-约界法的有效强度改进[J]. 吉林大学学报(工学版), 2021, 51(2): 597-603.
[15] 宫亚峰,宋加祥,谭国金,毕海鹏,刘洋,单承新. 多车桥梁动态称重算法[J]. 吉林大学学报(工学版), 2021, 51(2): 583-596.
Viewed
Full text


Abstract

Cited
  Shared   
  Discussed   
No Suggested Reading articles found!
版权所有 © 《吉林大学学报(工学版)》编辑部
地址：长春市人民大街5988号　电话：+86-431-85095297　传真：+86-431-85094074　E-mail: xbgxb@jlu.edu.cn
本系统由北京玛格泰克科技发展有限公司设计开发