考虑黏结-滑移效应的UHPC梁裂缝宽度计算方法

doi:10.13229/j.cnki.jdxbgxb.20230724

摘要/Abstract

摘要：

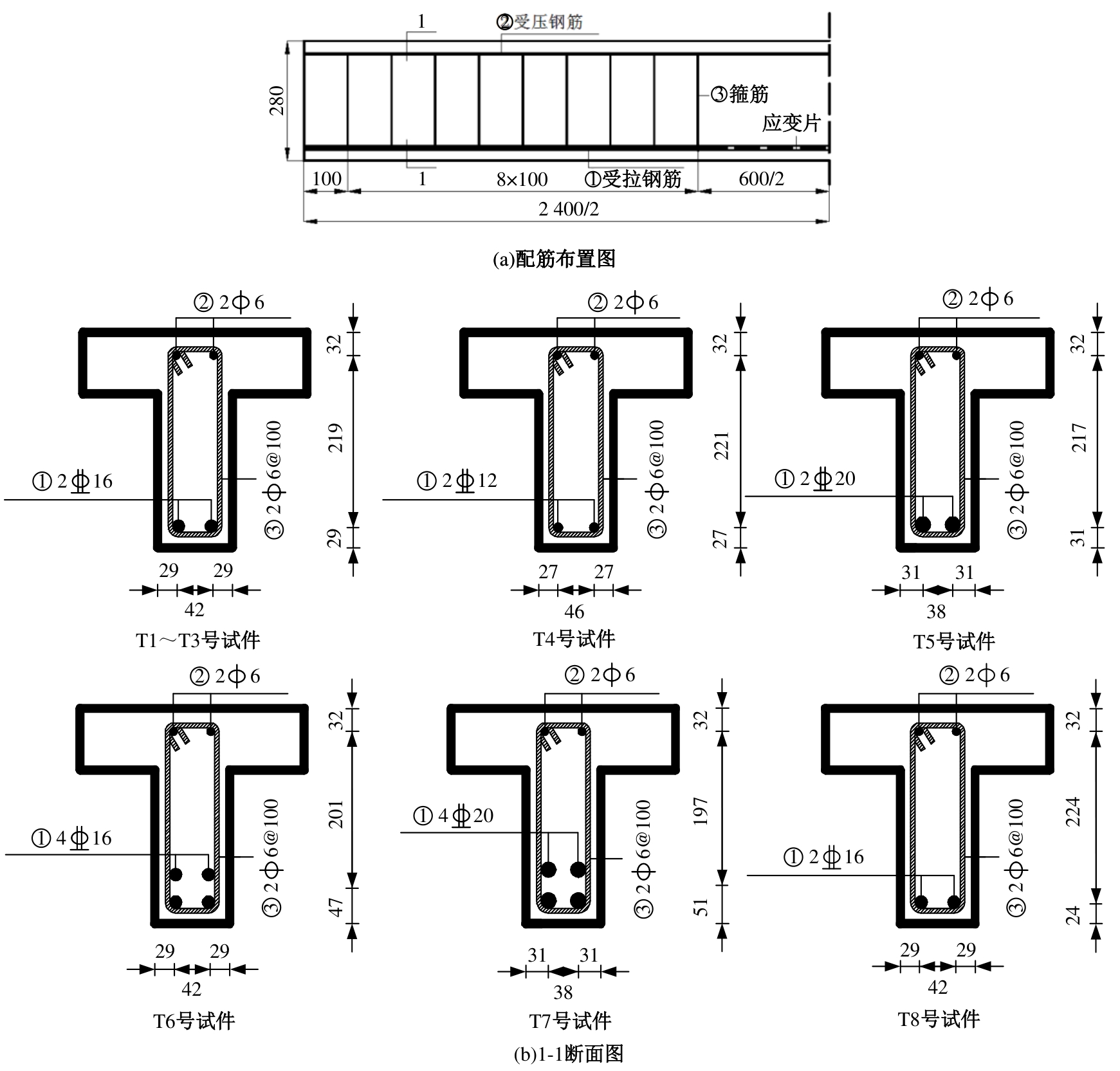
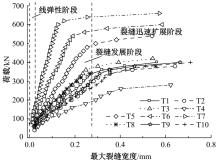
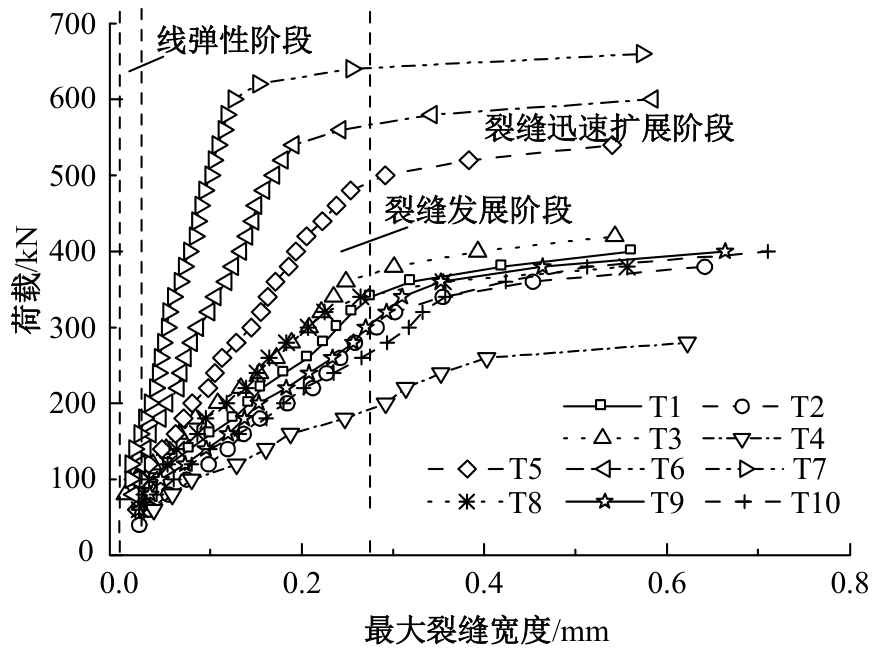
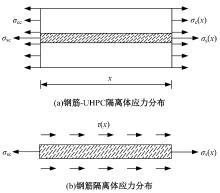
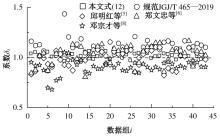
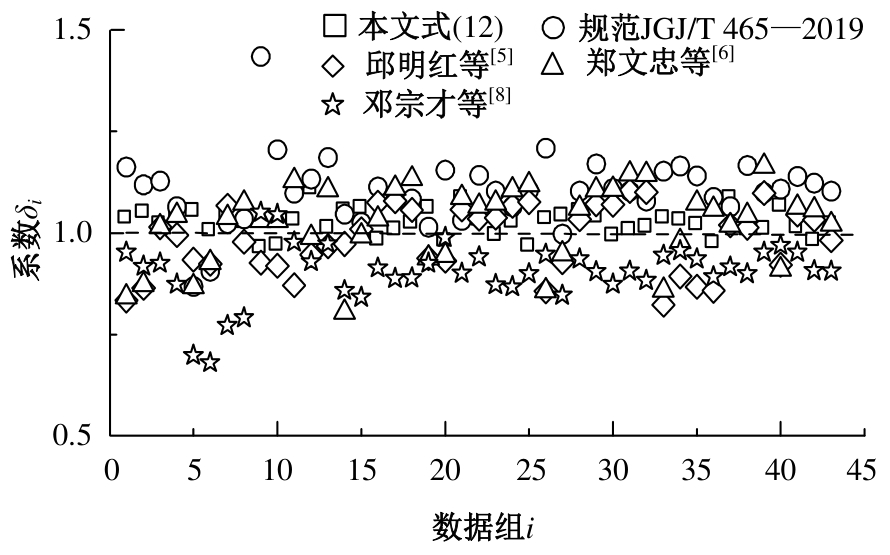
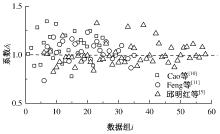
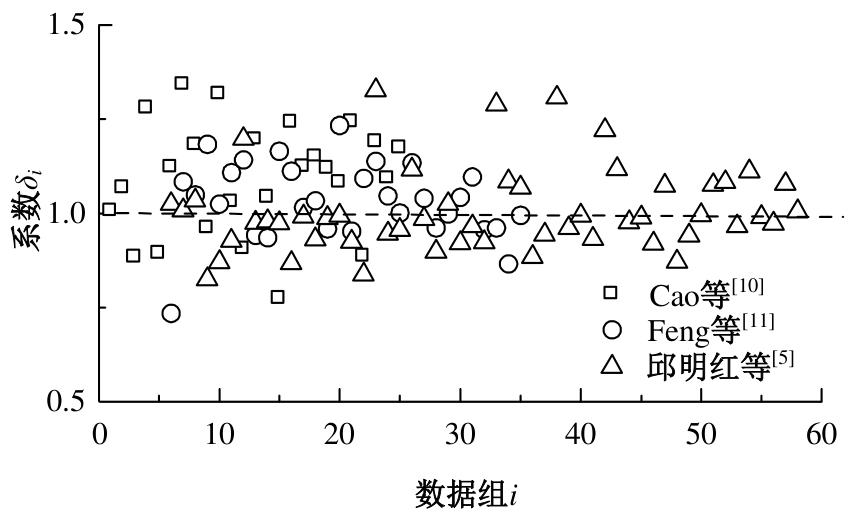
为建立适用于配筋超高性能混凝土（UHPC）梁的裂缝宽度计算公式，提出了考虑黏结-滑移效应的裂缝宽度计算方法。以钢纤维掺量、配筋率和保护层厚度为参变量，通过10片UHPC-T形截面梁的四点抗弯试验，研究了各参变量对试验梁破坏形态和最大裂缝宽度的影响规律。应用基于微元体建立的平衡与变形微分控制方程，结合考虑多影响因素的界面黏结-滑移关系，建立了配筋UHPC梁的裂缝宽度计算公式。通过与试验值、文献值对比，验证了裂缝宽度计算公式的正确性与适用性。结果表明：建立的裂缝宽度计算公式能充分体现钢纤维抗拉贡献和钢筋与UHPC界面间的黏结-滑移性能影响，其计算值与试验值吻合良好，能准确计算配筋UHPC梁的裂缝宽度。

关键词: 桥梁工程, 超高性能混凝土, 最大裂缝宽度, 四点抗弯试验, 黏结滑移, 微元体

Abstract:

To establish a crack width calculation formula applicable to reinforced ultra-high performance concrete （UHPC） beams， a crack width calculation method considering bond slip effects was proposed. Based on the four-point flexural tests of 10 UHPC-T beams with steel fiber content， reinforcement ratio and protective layer thickness as parameters， the effects of each parameter on the failure pattern and maximum crack width of the test beams were studied. The equations for calculating the crack width of reinforced UHPC beams were established by using the balance and deformation differential governing equations based on microelements and the interfacial bond slip relation considering many influential factors. The correctness and applicability of the formula for calculating crack width were verified by comparing with the experimental and literature values. The results show that the established formula can fully reflect the tensile contribution of steel fiber and the influence of interface bonding and sliding properties of steel bar and UHPC. The calculated values are in good agreement with the experimental values， and the crack widths of reinforced UHPC beams can be accurately calculated.

Key words: bridge engineering, ultra-high performance concrete （UHPC）, maximum crack width, four-point flexural tests, bond slip, microelements

中图分类号:

U443.32

孙永新,蔺鹏臻,杨子江,冀伟. 考虑黏结-滑移效应的UHPC梁裂缝宽度计算方法[J]. 吉林大学学报(工学版), 2024, 54(9): 2600-2608.

Yong-xin SUN,Peng-zhen LIN,Zi-jiang YANG,Wei JI. Calculation method for crack width of UHPC beams considering bond slip effect[J]. Journal of Jilin University(Engineering and Technology Edition), 2024, 54(9): 2600-2608.

图/表 13

表1

表2

表3

图1

图2

表4

表5

图3

图4

图5

图6

表6

图7

参考文献 21

1	朱劲松, 秦亚婷, 刘周强.预应力UHPC-NC组合梁截面优化设计[J].吉林大学学报: 工学版, 2023, 53(11): 3151-3159.
	Zhu Jin-song, Qin Ya-ting, Liu Zhou-qiang, et al. Section optimization design of prestressed UHPC-NC composite beams[J]. Journal of Jinlin University (Engineering and Technology Edition), 2023, 53(11): 3151- 3159.
2	邱明红, 邵旭东, 刘琼伟,等. UHPC局部受压承载力计算方法[J].交通运输工程报, 2021, 21(4): 116-129.
	Qiu Ming-hong, Shao Xu-dong, Liu Qiong-wei, et al. Calculation method of UHPC local compressive bearing capacity[J]. Journal of Traffic and Transportation Engineering, 2021, 21(4): 116-129.
3	Makita T, Brühwiler E. Tensile fatigue behavior of ultra-high performance fibre reinforced concrete (UHPFRC)[J]. Materials & Structures, 2014, 47(3):475-491.
4	Qi J, Wu Z, Ma Z J, et al. Pullout behavior of straight and hooked-end steel fibres in UHPC matrix with various embedded angles[J]. Construction and Building Materials, 2018, 191: 764-774.
5	邱明红, 邵旭东, 胡伟业, 等.钢筋UHPC受弯构件裂缝宽度计算方法研究[J].土木工程学报, 2020, 53(10): 89-98.
	Qiu Ming-hong, Shao Xu-dong, Hu Wei-ye, et al. Calculation method for crack width of reinforced UHPC flexural components[J]. China Civil Engineering Journal, 2020, 53(10): 89-98.
6	郑文忠, 李莉, 卢珊珊. 钢筋活性粉末混凝土简支梁正截面受力性能试验研究[J]. 建筑结构学报, 2011, 52(6):125-134.
	Deng Wen-zhong, Li Li, Lu Shan-shan. Experimental research on mechanical performance of normal section of reinforced reactive powder concrete beam[J]. Journal of Building Structure, 2011, 52(6): 125-134.
7	徐海宾, 邓宗才. UHPC梁开裂弯矩和裂缝试验[J].哈尔滨工业大学学报, 2014, 46(4): 87-92.
	Xu Hai-bin, Deng Zong-cai. Cracking moment and crack width of ultra-high performance concrete beams[J]. Journal of Harbin Engineering University, 2014, 46(4): 87-92.
8	邓宗才, 肖锐, 徐海宾, 等. 高强钢筋超高性能混凝土梁的使用性能研究[J]. 哈尔滨工业大学学报, 2015, 36(10): 1335-1340.
	Deng Zong-cai, Xiao Rui, Xu Hai-bin, et al. Serviceability research of ultra-high performance concrete beams reinforced with high strength steel bars[J]. Journal of Harbin Engineering University, 2015, 36(10): 1335-1340.
9	Stürwald S, Fehling E. Design of reinforced UHPFRC in flexure[C]∥Proceedings of Hipermat 2012 3rd International Symposium on UHPC and Nanotechnology for High Performance Construction Materials. Kassel: Kassel, Germany, 2012: 443-450.
10	Cao X, Ren Y C, Zhang L, et al. Flexural behavior of ultra-high-performance concrete beams with various types of rebar[J]. Composite Structures, 2022, 292: No.115674.
11	Feng Z, Li C X, Yoo D Y, et al. Flexural and cracking behaviors of reinforced UHPC beams with various reinforcement ratios and fiber contents[J]. Engineering Structures, 2021, 248: No.113266.
12	. National addition to eurocode 2-design of concrete structures: specific rules for ultra-high performance fibre reinforced concrete [S].
13	程东辉, 范永萱, 王彦松. RC类活性粉末混凝土钢筋粘结滑移本构模型[J].吉林大学学报: 工学版, 2021, 51(4): 1317-1330.
	Cheng Dong-hui, Fan Yong-xuan, Wang Yan-song. Bond-slip constitutive model of steel bars and reactive powder concrete under standard curing[J]. Journal of Jinlin University (Engineering and Technology Edition), 2021, 51(4): 1317-1330.
14	Khaksefidi S, Ghalehnovi M, Debrito J. Bond behaviour of high-strength steel rebars in normal (NSC) and ultra-high performance concrete (UHPC)[J]. Journal of Building Engineering, 2021, 33: No.101592.
15	邱明红, 邵旭东, 胡伟业, 等. 钢筋UHPC矩形截面受弯构件的钢筋应力简化计算[J]. 中国公路学报, 2021, 34(8): 106-117.
	Qiu Ming-hong, Shao Xu-dong, Hu Wei-ye, et al. Simplified calculation of reinforcement stress in reinforced UHPC bending members with rectangular sections[J]. China Journal of Highway and Transport, 2021, 34(8): 106-117.
16	徐明雪, 梁兴文, 汪萍, 等.超高性能混凝土梁正截面受弯承载力理论研究[J].工程力学, 2019, 36(8): 70-78.
	Xu Ming-xue, Liang Xing-wen, Wang Ping, et al. The oretical Investigation on normal section flexural capacity of UHPC beams[J]. Engineering Mechanics, 2019, 36(8): 70-78.
17	赵国藩, 王清湘. 钢筋混凝土构件裂缝宽度分析的应力图形和计算模式[J]. 大连工学院学报, 1984(4): 87-94.
	Zhao Guo-fan, Wang Qing-xiang. Stress distribution and calculation formula for crack width analysis of reinforced concrete members[J]. Journal of Dalian Institute of Technology, 1984(4): 87-94.
18	贾方方, 安明喆, 余自若, 等. 钢筋与活性粉末混凝土黏结性能的梁式试验研究[J].铁道学报, 2012, 34(6): 83-87.
	Jia Fang-fang, An Ming-zhe, Yu Zi-ruo, et al. Beam test of bond behavior between steel bars and reactive powder concrete[J]. Journal of the China Railway Society, 2012, 34(6): 83-87.
19	王景全, 戚家南, 刘加平.基于细观本构模型的UHPC梁受弯全过程分析[J].建筑结构学报, 2020, 41(9): 137-144.
	Wang Jing-quan, Qi Jia-nan, Liu Jia-ping. Flexural analysis of UHPC beams based on a mesoscale constitutive model[J]. Journal of Building Structure, 2020, 41(9): 137-144.
20	周建民, 王眺, 赵勇, 等. 高强钢筋混凝土受弯构件裂缝宽度计算方法的研究[J].土木工程学报, 2010, 43(9): 69-76.
	Zhou Jian-min, Wang Tiao, Zhao Yong, et al. Research on the calculation of crack width for RC flexural member using high-strength bars[J]. China Civil Engineering Journal, 2010, 43(9): 69-76.
21	孙永新, 蔺鹏臻, 杨子江, 等. 考虑多影响因素的配筋UHPC梁裂缝宽度计算方法[J].东南大学学报:自然科学版, 2023,53(4): 628-636.
	Sun Yong-xin, Lin Peng-zhen, Yang Zi-jiang, et al. Calculation method for crack width of reinforced UHPC beams considering multiple influencing factors[J]. Journal of Southeast University (Natural Science Edition), 2023, 53(4): 628-636.

相关文章 15

[1]	朱劲松,佟欣瑶,刘晓旭. 装配式小箱梁桥超高性能混凝土免支模湿接缝抗弯性能[J]. 吉林大学学报(工学版), 2024, 54(9): 2568-2580.
[2]	薛宇欣,周勇军,王业路,范凯翔,赵煜. 基于悬锤系统的简支梁桥冲击系数测试方法适用性[J]. 吉林大学学报(工学版), 2024, 54(9): 2557-2567.
[3]	郭雪莲,韩万水,王涛,周恺,张修石,张书颖. 大件车通行弯桥抗倾覆稳定安全系数评估方法[J]. 吉林大学学报(工学版), 2024, 54(8): 2229-2237.
[4]	肖林,魏欢博,卫星,康志锐. 钢混组合梁栓钉锈胀下混凝土板开裂行为数值分析[J]. 吉林大学学报(工学版), 2024, 54(7): 1958-1965.
[5]	张春雷,邵长宇,苏庆田,戴昌源. 球扁钢肋钢纤维混凝土组合桥面板正弯矩受力性能试验[J]. 吉林大学学报(工学版), 2024, 54(6): 1634-1642.
[6]	张彦玲,贾云飞,贾晓远,郑旺,李运生. 装配式小箱梁桥内力横向分布系数建议公式[J]. 吉林大学学报(工学版), 2024, 54(6): 1688-1700.
[7]	黄汉辉,陈康明,吴庆雄. 钢管混凝土桁式弦杆组合连续梁抗弯性能[J]. 吉林大学学报(工学版), 2024, 54(6): 1665-1676.
[8]	邵长江,崔皓蒙,漆启明,庄卫林. 近断层大跨RC轻柔拱桥纵向阻尼器减震研究[J]. 吉林大学学报(工学版), 2024, 54(5): 1355-1367.
[9]	赵秋,陈鹏,赵煜炜,余澳. 台后设置拱形结构的无缝桥梁整体受力性能[J]. 吉林大学学报(工学版), 2024, 54(4): 1016-1027.
[10]	张洪,朱志伟,胡天宇,龚燕峰,周建庭. 基于改进YOLOv5s的桥梁螺栓缺陷识别方法[J]. 吉林大学学报(工学版), 2024, 54(3): 749-760.
[11]	韩智强,谢刚,卓亚娟,骆佐龙,李华腾. 基于车轮-桥面相干激励的大跨连续梁桥振动响应[J]. 吉林大学学报(工学版), 2024, 54(2): 436-444.
[12]	杨国俊,齐亚辉,石秀名. 基于数字图像技术的桥梁裂缝检测综述[J]. 吉林大学学报(工学版), 2024, 54(2): 313-332.
[13]	谭国金,欧吉,艾永明,杨润超. 基于改进DeepLabv3+模型的桥梁裂缝图像分割方法[J]. 吉林大学学报(工学版), 2024, 54(1): 173-179.
[14]	龙关旭,张修石,辛公锋,王涛,杨干. 融合机器视觉的桥梁动态称重方法[J]. 吉林大学学报(工学版), 2024, 54(1): 188-197.
[15]	卫星,高亚杰,康志锐,刘宇辰,赵骏铭,肖林. 低温环境下栓钉环焊缝焊接残余应力场数值模拟[J]. 吉林大学学报(工学版), 2024, 54(1): 198-208.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

ρ_f/%	f_cu/MPa	f_c/MPa	f_t/MPa	E_c/（10⁴MPa）
1	121.22	83.72	6.35	4.1
2	133.71	89.14	7.84	4.2
3	141.53	97.82	9.32	4.4

编号	ρ_f/%	纵筋配置	ρ_s/%	c/mm
T1	2	216	1.60	15
T2	1	216	1.60	15
T3	3	216	1.60	15
T4	2	212	0.89	15
T5	2	220	2.51	15
T6	2	416	3.20	15
T7	2	420	5.02	15
T8	2	216	1.60	10
T9	2	216	1.60	20
T10	2	216	1.60	25

梁号	M_u/ （kN?m）	M_cr/ （kN?m）	M_0.2/ （kN?m）	M_0.2/M_u	破坏形态
T1	136.9	21.1	98.12	0.72	适筋
T2	128.6	19.4	83.88	0.65	适筋
T3	145.5	21.9	119.52	0.82	适筋
T4	97.9	16.7	61.24	0.63	适筋
T5	193.1	20.1	159.2	0.82	界限
T6	218.6	21.1	-	-	超筋
T7	251.4	28.2	-	-	超筋
T8	129.0	14.2	145.12	0.82	适筋
T9	138.6	20.0	92.20	0.67	适筋
T10	139.3	20.6	83.36	0.60	适筋

梁号	F_max/kN	w_max/mm	l_mt/mm	s/（10^-6mm?N^-1）
T1	321.4	0.26	64.4	1.06
T2	311.3	0.29	66.1	1.04
T3	334.3	0.24	62.5	1.07
T4	218.6	0.32	81.1	2.26
T5	454.9	0.23	57.6	0.61
T6	529.2	0.18	49.5	0.40
T7	601.3	0.13	42.2	0.23
T8	298.4	0.24	58.5	0.87
T9	317.5	0.30	73.8	1.23
T10	324.1	0.34	81.8	1.40

参数	本文式（12）	既有方法
参数	本文式（12）	JGJ/T465-2019	邱明红等^［5］	郑文忠等^［6］	邓宗才等^［8］
均值	1.02	1.10	0.98	1.02	0.91
变异系数	0.05	0.11	0.08	0.09	0.07