基于悬锤系统的简支梁桥冲击系数测试方法适用性

doi:10.13229/j.cnki.jdxbgxb.20221390

吉林大学学报(工学版) ›› 2024, Vol. 54 ›› Issue (9): 2557-2567.doi: 10.13229/j.cnki.jdxbgxb.20221390

• 交通运输工程·土木工程 • 上一篇

基于悬锤系统的简支梁桥冲击系数测试方法适用性

薛宇欣¹(),周勇军¹(),王业路²,范凯翔³,赵煜¹

^1.长安大学公路学院，西安 710064
^2.青岛理工大学土木工程学院，山东青岛 266033
^3.湖北省交通规划设计院股份有限公司，武汉 430051

收稿日期:2022-11-01 出版日期:2024-09-01 发布日期:2024-10-28
通讯作者: 周勇军 E-mail:2021021017@chd.edu.cn;zyj@chd.edu.cn
作者简介:薛宇欣（1996-），女，博士研究生.研究方向：车桥耦合振动.E-mail：2021021017@chd.edu.cn
基金资助:
国家重点研发计划项目(2021YFB2601000);国家自然科学基金项目(51978063);中央高校基本科研业务费项目(300102214708)

Application of dynamic load allowance test method of simply supported girder bridge based on suspension hammer system

Yu-xin XUE¹(),Yong-jun ZHOU¹(),Ye-lu WANG²,Kai-xiang FAN³,Yu ZHAO¹

^1.School of Highway，Chang'an University，Xi'an 710064，China
^2.College of Civil Engineering，Qingdao University of Technology，Qingdao 266033，China
^3.Hubei Communications Planning and Design Institute Co. ，Ltd. ，Wuhan 430051，China

Received:2022-11-01 Online:2024-09-01 Published:2024-10-28
Contact: Yong-jun ZHOU E-mail:2021021017@chd.edu.cn;zyj@chd.edu.cn

摘要/Abstract

摘要：

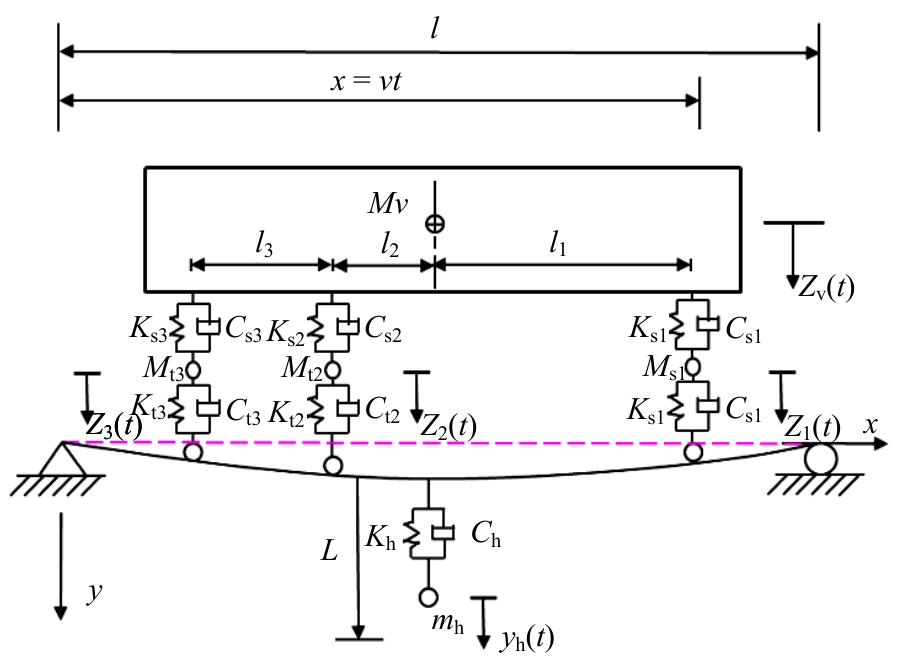
为研究悬锤系统在桥梁动力测试中的应用，以标准跨径简支梁/板桥为对象，采用理论推导、数值模拟与试验验证相结合的方法开展研究。首先，根据达朗贝尔原理推导了车-桥-悬锤系统耦合振动理论方程；然后，基于ANSYS软件编制分析程序进行数值计算，研究悬挂长度、铁丝直径、弹性模量以及悬锤质量对悬锤法测试冲击系数结果的影响，并与支架法测试结果对比，结合响应面分析，针对不同桥型提出了悬锤系统参数选型建议；最后，选取一座30 m简支箱梁桥进行动载试验，分别采用支架法与悬锤法测试挠度冲击系数，验证本文参数选型。结果表明：铁丝直径和悬锤质量交互作用显著；为满足悬锤法与支架法测量冲击系数差值小于5%的要求，铁丝直径以及悬锤质量的最佳取值应随悬挂长度增加而增大。

关键词: 桥梁工程, 简支梁桥, 冲击系数, 动挠度, 悬锤系统

Abstract:

To explore the application of hammer system in bridge dynamic test， simply supported bridge with standard span were selected. Research on dynamic load allowance （DLA） test of simply supported bridge were carried out， adopting theoretical derivation， numerical simulation and experimental verification. Firstly， the vehicle-bridge-suspension system coupled vibration theoretical equation was derived according to d'Alembert principle. Then， the analysis program was compiled based on ANSYS to obtain the DLAs of suspension hammer method. The influence of suspension length， wire diameter， elastic modulus and suspension hammer mass on the accuracy of DLA were discussed， comparing with the results of scaffolding method. Furthermore， combining with response surface methodology， the suggested value of suspension hammer system parameters about different bridges types were proposed. Finally， a 30 m simply supported box girder bridge was tested under dynamic load. Dynamic deflection of the bridge was tested by scaffolding and suspension hammer method to verify the suggested value. Results demonstrated that there is a significant interaction between wire diameter and suspension hammer mass. To satisfy the difference of less than 5% between deflection DLA measured by suspension hammer and scaffolding method， the optimal values of wire diameter and suspension hammer mass should increase with wire length.

Key words: bridge engineering, simply supported girder bridge, dynamic load allowance, dynamic deflection, suspension hammer system

中图分类号:

薛宇欣,周勇军,王业路,范凯翔,赵煜. 基于悬锤系统的简支梁桥冲击系数测试方法适用性[J]. 吉林大学学报(工学版), 2024, 54(9): 2557-2567.

Yu-xin XUE,Yong-jun ZHOU,Ye-lu WANG,Kai-xiang FAN,Yu ZHAO. Application of dynamic load allowance test method of simply supported girder bridge based on suspension hammer system[J]. Journal of Jilin University(Engineering and Technology Edition), 2024, 54(9): 2557-2567.

图/表 12

图1

表1

图2

图3

图4

图5

图6

表2

图7

表3

图8

表4

两种测试方法1+μ对比"

车速/（km·h^-1）	①支架法（ $1 + μ$ ）	②悬锤法（ $1 + μ c$ ）	（①~②）/①）/（%）	差值平均值/%
20	1.171	1.080	7.82	4.99
30	1.073	1.006	6.25
40	1.085	1.041	4.06
50	1.147	1.081	5.76
60	1.102	1.113	-1.06

表4

参考文献 25

1	中华人民共和国交通运输部. 2023年交通运输行业发展统计公报[N]. 中国交通报, 2024-6-18.
	Ministry of Transport of the People's Republic of China.Ministry of transport statistical bulletin on the development of transportation industry in 2023[N]. China Transport News, 2024-06-18.
2	.公路桥梁荷载试验规程 [S].
3	周勇军, 蔡军哲, 石雄伟, 等. 基于加权法的桥梁冲击系数计算方法[J]. 交通运输工程学报, 2013, 13(4): 29-36.
	Zhou Yong-jun, Cai Jun-zhe, Shi Xiong-wei, et al. Computing method of bridge impact factor based on weighted method[J]. Journal of Traffic and Transportation Engineering, 2013, 13(4): 29-36.
4	周勇军, 薛宇欣, 李冉冉,等. 桥梁冲击系数理论研究和应用进展[J]. 中国公路学报, 2021, 34(4): 31-50.
	Zhou Yong-jun, Xue Yu-xin, Li Ran-ran, et al. State-of-the-art of theory and applications of bridge dynamic load allowance[J]. China Journal of Highway and Transport, 2021, 34(4): 31-50.
5	熊先才, 章鹏, 苻欲梅, 等. 光电液位传感器及其在桥梁挠度自动测量中的应用[J]. 地震工程与工程振动, 2006, 26(4): 260-264.
	Xiong Xian-cai, Zhang Peng, Fu Yu-mei, et al. Optoelectronic liquid-level sensor and its application for automatically measuring bridge deflection[J]. Earthquake Engineering and Engineering Vibration, 2006,26(4):260-264.
6	邵新星, 黄金珂, 员方, 等. 基于视觉的桥梁挠度测量方法与研究进展[J]. 实验力学, 2021, 36(1):29-42.
	Shao Xin-xing, Huang Jin-ke, Yuan Fang, et al. Measurement method and recent progress of vision-based deflection measurement of bridges[J]. Journal of Experimental Mechanics, 2021,36(1):29-42.
7	Huang J, Shao X X, Yang F J. Measurement method and recent progress of vision-based deflection measurement of bridges: a technical review[J]. Optical Engineering, 2022, 61(7): No. 070901.
8	蓝章礼,杨小帆.非接触式张力线桥梁挠度测量系统[J].仪器仪表学报, 2008, 29(5): 1058-1062.
	Lan Zhang-li, Yang Xiao-fan. Non-contact bridge deflection measurement system using weighted- streched-wire[J]. Chinese Journal of Scientific Instrument, 2008, 29(5): 1058-1062.
9	王业路, 周勇军, 高徐军, 等. 基于预紧弹簧系统的桥梁挠度冲击系数量测方法[J]. 中国公路学报, 2022, 35(10): 172-182.
	Wang Ye-lu, Zhou Yong-jun, Gao Xu-jun, et al. Measurement method of the bridge deflection dynamic load allowance based on preloaded spring system[J]. China Journal of Highway and Transport, 2022, 35(10): 172-182.
10	Dong Y, Wang J Q, Ren W X, et al. A plastic optical fiber sensing system for bridge deflection measurement[J]. Sensors,2020,20(2):No.s20020480.
11	Alipour M, Washlesky S J, Harris D K. Field development and laboratory evaluation of 2D digital image correlation for deflection sensing in complex environments[J]. Journal of Bridge Engineering, 2019,24(4): No. 04019010.
12	Garg P, Moreu F, Ozdagli A, et al. Noncontact dynamic displacement measurement of structure using a moving laser doppler vibrometer[J]. Journal of Bridge Engineering, 2019, 24 (9): No.4019089.
13	Nie G Y, Bodda S S, Gupta A. Computer-vision- based vibration tracking using a digital camera: a sparse-optical- flow-based target tracking method[J]. Sensors, 2022, 22(18): No.s22186869.
14	Cha G C, Park S, Oh T. A terrestrial lidar-based detection of shape deformation for maintenance of bridge structure[J]. Journal of Construction Engineering and Management, 2019, 145(12): No.4019075.
15	Xue M S, Yi T H, Qu C X, et al. Rapid estimation of bridge key deflection through optimized substructure impact testing[J]. Journal of Bridge Engineering,2022, 27(10): No. 4022088.
16	钟继卫, 王波, 王翔, 等. 桥梁智能检测技术研究与应用[J]. 桥梁建设, 2019, 49(): 1-6.
	Zhong Ji-wei, Wang Bo, Wang Xiang, et al. Research of bridge intelligent inspection technology and application[J]. Bridge Construction, 2019,49(Sup.1):1-6.
17	李万恒, 申林, 王少鹏, 等. 基于多阶段分区域动力测试的桥梁结构损伤评估[J]. 吉林大学学报: 工学版, 2019, 49(3): 773-780.
	Li Wan-heng, Shen Lin, Wang Shao-peng, et al. Damage assessment of bridge construction on multi-stage subregion mobile test[J]. Journal of Jilin University (Engineering and Technology Edition), 2019, 49(3): 773-780.
18	Yang D, Zhang S Q, Wang S, et al. Real-time illumination adjustment for video deflectometers[J]. Structure Control & Health Monitoring, 2022,29(5):No.e2930.
19	王磊, 陈顺超, 袁胜涛, 等. 基于悬挂吊锤的桥梁动挠度测试[J]. 科学技术与工程, 2021, 21(21): 9108-9115.
	Wang Lei, Chen Shun-chao, Yuan Sheng-tao, et al. Test of bridge dynamic deflection based on suspended hammer[J]. Science Technology and Engineering, 2021, 21(21): 9108-9115.
20	周勇军, 薛宇欣, 高徐军, 等. 基于模态叠加法的公路简支梁桥动力放大系数研究[J]. 交通运输工程学报, 2023, 23(6): 146-155.
	Zhou Yong-jun, Xue Yu-xin, Gao Xu-jun, et al. Research on dynamic amplification factor of highway simply supported girder bridge based on modal superposition method[J]. Journal of Traffic and Transportation Engineering, 2023, 23(6): 146-155.
21	周勇军, 赵洋, 赵煜, 等. 基于动载试验荷载效率的简支梁桥冲击系数研究[J]. 振动与冲击, 2021, 40(20): 207-216.
	Zhou Yong-jun, Zhao Yang, Zhao Yu, et al. A study on dynamic load allowance of a simply supported girder bridge based on load efficiency of a dynamic load test[J]. Journal of Vibration and Shock,2021,40(20): 207-216.
22	韩智强, 谢刚, 周勇军, 等. 曲线桥梁车桥耦合振动数值分析方法[J].吉林大学学报: 工学版, 2023, 53(2): 515-522.
	Han Zhi-qiang, Xie Gang, Zhou Yong-jun, et al. Numerical analysis method of vehicle-bridge coupling vibration of curved bridge[J]. Journal of Jilin University (Engineering and Technology Edition), 2023, 53(2): 515-522.
23	沈火明, 肖新标. 求解车桥耦合振动问题的一种数值方法[J]. 西南交通大学学报, 2003, 38(6): 658-662.
	Shen Huo-ming, Xiao Xin-biao. Numerical method for vehicle bridge coupled vibrations[J]. Journal of Southwest Jiaotong University, 2003,38(6):658-662.
24	Won K L, Hae D P. Chaotic dynamics of a harmonically excited spring-pendulum system with internal resonance[J]. Nonlinear Dynamics, 1997, 14(3): 211 -229.
25	姚玉权, 仰建岗, 高杰, 等. 基于性能-费用模型的厂拌再生沥青混合料优化设计[J]. 吉林大学学报:工学版, 2022, 52(3): 585-595.
	Yao Yu-quan, Yang Jian-gang, Gao Jie, et al. Optimal design on recycled hot-mix asphalt mixture based on performance-cost model[J]. Journal of Jilin University (Engineering and Technology Edition), 2022,52(3): 585-595.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

桥型	跨径/m	截面面积/m²	质量m/kg	截面惯性矩I_yy/m⁴
简支T梁桥	20	0.754 0	1 922.328 5	0.190 4
	25	0.806 0	2 054.908 1	0.276 4
	30	0.889 8	2 498.050 1	0.538 8
	35	0.979 8	2 268.611 5	0.891 2
	40	1.072 0	2 733.021 1	0.909 5
简支箱梁桥	20	1.112 8	2 837.090 1	0.186 4
	25	1.209 0	3 082.195 2	0.279 0
	30	1.307 6	3 333.571 9	0.396 0
	35	1.634 6	4 167.321 8	0.589 7
	40	1.761 1	4 489.726 5	0.781 9
简支空心板桥	10	0.391 8	998.878 4	0.016 1
	13	0.426 8	1 088.109 5	0.024 5
	16	0.514 3	1 311.187 3	0.037 5
	20	0.527 3	1 344.330 3	0.055 2

响应面分析区间一			响应面分析区间二
自变量	取值	BBD水平	自变量	取值	BBD水平
A：铁丝长度/m	5~30	5，17.5，30	A：铁丝长度/m	5~30	5，17.5，30
B：铁丝直径/mm	0.1~1	0.1，0.55，1	B：铁丝直径/mm	1~2.5	1，1.75，2.5
C：悬锤质量/kg	1~2	1，1.5，2	C：悬锤质量/kg	2~4	2，3，4

桥型	跨径/m	铁丝长度/m	铁丝直径/ mm	悬锤质量/ kg	跨径/m	铁丝长度/ m	铁丝直径/ mm	悬锤质量/kg	跨径/m	铁丝长度/ m	铁丝直径/ mm	悬锤质量/ kg
简支空心板桥	10	5	0.5	1.0~1.2	13	5	0.5	1.2	16	5	0.5	2.0
		10	0.6	1.2		10	0.6	1.2		10	0.6	1.0
		15	0.8	1.4		15	1.0	1.2		15	0.8	1.2
		20	1.0	1.5		20	1.2	1.4		20	1.0	1.4
		25	1.2	2.0		25	1.4	1.5		25	1.2	1.5
		30	1.5	2.5		30	1.5	1.8		30	1.5	1.6
	20	5	0.3	2.0
		10	0.4	1.5
		15	0.5	1.5~1.6
		20	0.5	1.8
		25	0.7	2.0
		30	0.8	2.0
简支T梁桥	20	5	0.5	1.5	25	5	0.5	1.5	30	5	0.5	1.5
		10	0.7	1.6		10	0.8	1.6		10	0.6	1.5
		15	1.0	1.8		15	0.8	1.6		15	0.8	1.6~1.8
		20	1.2	2.0		20	1.0	1.8		20	1.0	1.8~2.0
		25	1.5	2.2		25	1.0	2.0		25	1.2	2.0
		30	1.6	2.5		30	1.2	2.0		30	1.5	2.0
	35	5	0.5	1.5	40	5	2.0	1.5
		10	0.6	1.6		10	1.5	1.6
		15	0.8	1.8		15	1.2	2.0~2.4
		20	1.0	2.0		20	1.0	2.2~2.4
		25	1.2	2.0		25	0.8	2.5
		30	1.5	2.4~2.5		30	0.5	2.5
简支箱梁桥	20	5	0.6	1.5	25	5	0.5	1.5	30	5	0.5	1.5
		10	0.7	1.6		10	0.6	1.6		10	0.7	1.6
		15	0.9/1.0	1.8~2.0		15	0.8	1.6		15	0.8	1.8
		20	1.0	2.0		20	1.0	1.6~1.8		20	1.0	2.0
		25	1.4	2.0		25	1.5	2.0		25	1.2	2.0
		30	1.5	2.0		30	1.5	2.5		30	1.5	2.4
	35	5	0.7	1.4	40	5	1.0	1.5
		10	0.9/1.0	1.5		10	1.2~1.4	1.6
		15	1.2	1.5		15	1.5	1.8
		20	1.5	1.6		20	1.8	2.0
		25	1.6	2.0~2.2		25	2.0	2.2
		30	1.8	2.2		30	2.0	2.5

[1]	郭雪莲,韩万水,王涛,周恺,张修石,张书颖. 大件车通行弯桥抗倾覆稳定安全系数评估方法[J]. 吉林大学学报(工学版), 2024, 54(8): 2229-2237.
[2]	肖林,魏欢博,卫星,康志锐. 钢混组合梁栓钉锈胀下混凝土板开裂行为数值分析[J]. 吉林大学学报(工学版), 2024, 54(7): 1958-1965.
[3]	张春雷,邵长宇,苏庆田,戴昌源. 球扁钢肋钢纤维混凝土组合桥面板正弯矩受力性能试验[J]. 吉林大学学报(工学版), 2024, 54(6): 1634-1642.
[4]	张彦玲,贾云飞,贾晓远,郑旺,李运生. 装配式小箱梁桥内力横向分布系数建议公式[J]. 吉林大学学报(工学版), 2024, 54(6): 1688-1700.
[5]	黄汉辉,陈康明,吴庆雄. 钢管混凝土桁式弦杆组合连续梁抗弯性能[J]. 吉林大学学报(工学版), 2024, 54(6): 1665-1676.
[6]	邵长江,崔皓蒙,漆启明,庄卫林. 近断层大跨RC轻柔拱桥纵向阻尼器减震研究[J]. 吉林大学学报(工学版), 2024, 54(5): 1355-1367.
[7]	赵秋,陈鹏,赵煜炜,余澳. 台后设置拱形结构的无缝桥梁整体受力性能[J]. 吉林大学学报(工学版), 2024, 54(4): 1016-1027.
[8]	张洪,朱志伟,胡天宇,龚燕峰,周建庭. 基于改进YOLOv5s的桥梁螺栓缺陷识别方法[J]. 吉林大学学报(工学版), 2024, 54(3): 749-760.
[9]	韩智强,谢刚,卓亚娟,骆佐龙,李华腾. 基于车轮-桥面相干激励的大跨连续梁桥振动响应[J]. 吉林大学学报(工学版), 2024, 54(2): 436-444.
[10]	杨国俊,齐亚辉,石秀名. 基于数字图像技术的桥梁裂缝检测综述[J]. 吉林大学学报(工学版), 2024, 54(2): 313-332.
[11]	谭国金,欧吉,艾永明,杨润超. 基于改进DeepLabv3+模型的桥梁裂缝图像分割方法[J]. 吉林大学学报(工学版), 2024, 54(1): 173-179.
[12]	龙关旭,张修石,辛公锋,王涛,杨干. 融合机器视觉的桥梁动态称重方法[J]. 吉林大学学报(工学版), 2024, 54(1): 188-197.
[13]	卫星,高亚杰,康志锐,刘宇辰,赵骏铭,肖林. 低温环境下栓钉环焊缝焊接残余应力场数值模拟[J]. 吉林大学学报(工学版), 2024, 54(1): 198-208.
[14]	安然,王有志. 剪力钉连接件拉剪共同作用抗剪性能[J]. 吉林大学学报(工学版), 2023, 53(9): 2554-2562.
[15]	左新黛,张劲泉,赵尚传. 在役混凝土T梁疲劳刚度退化及寿命预测方法[J]. 吉林大学学报(工学版), 2023, 53(9): 2563-2572.

基于悬锤系统的简支梁桥冲击系数测试方法适用性

Application of dynamic load allowance test method of simply supported girder bridge based on suspension hammer system

RICH HTML

PDF (PC)

摘要/Abstract

引用本文

使用本文

图/表 12

参考文献 25

相关文章 15

Metrics

本文评价

推荐阅读 0