结合黏菌觅食行为的改进多元宇宙算法

doi:10.13229/j.cnki.jdxbgxb20210649

摘要/Abstract

摘要：

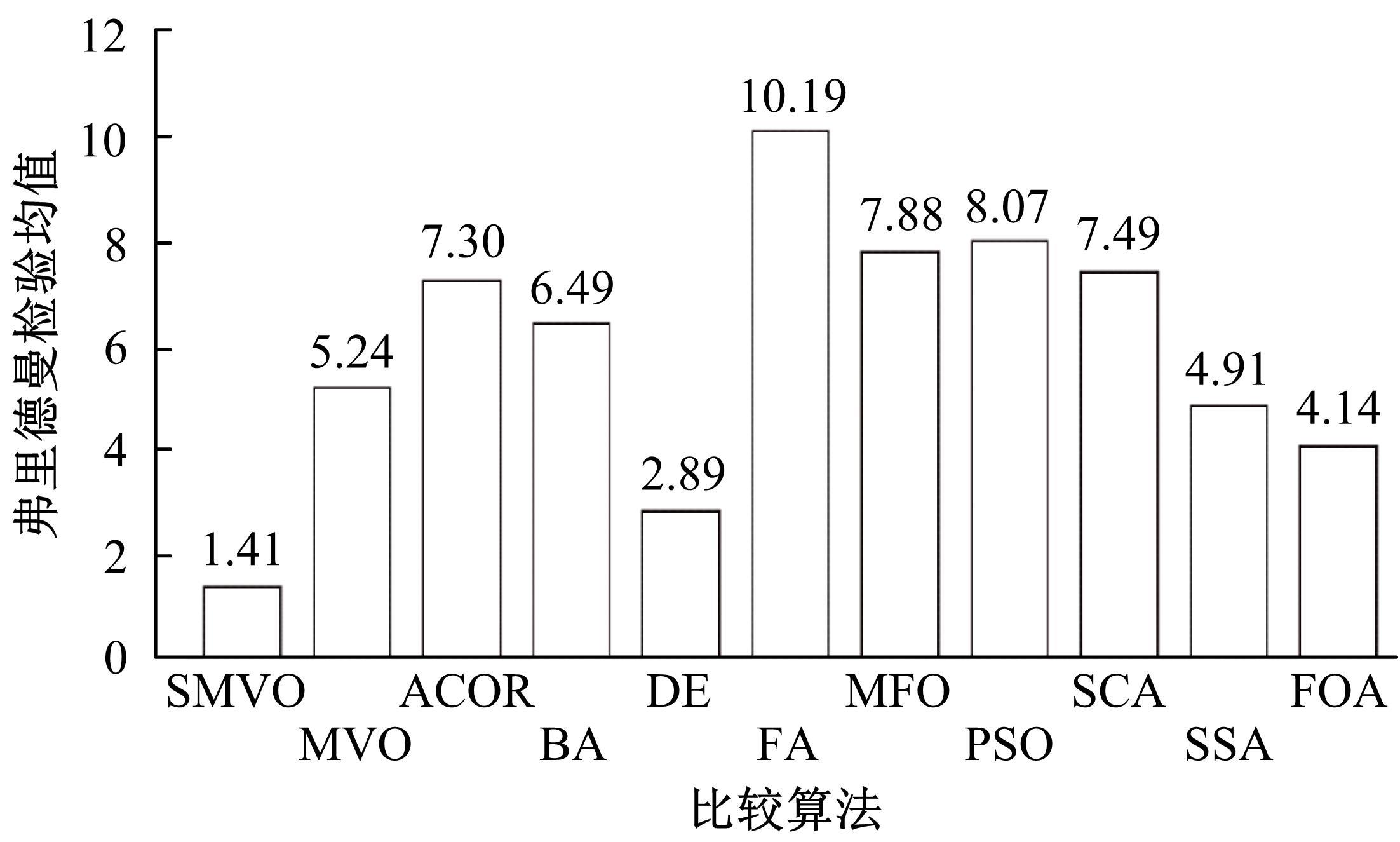
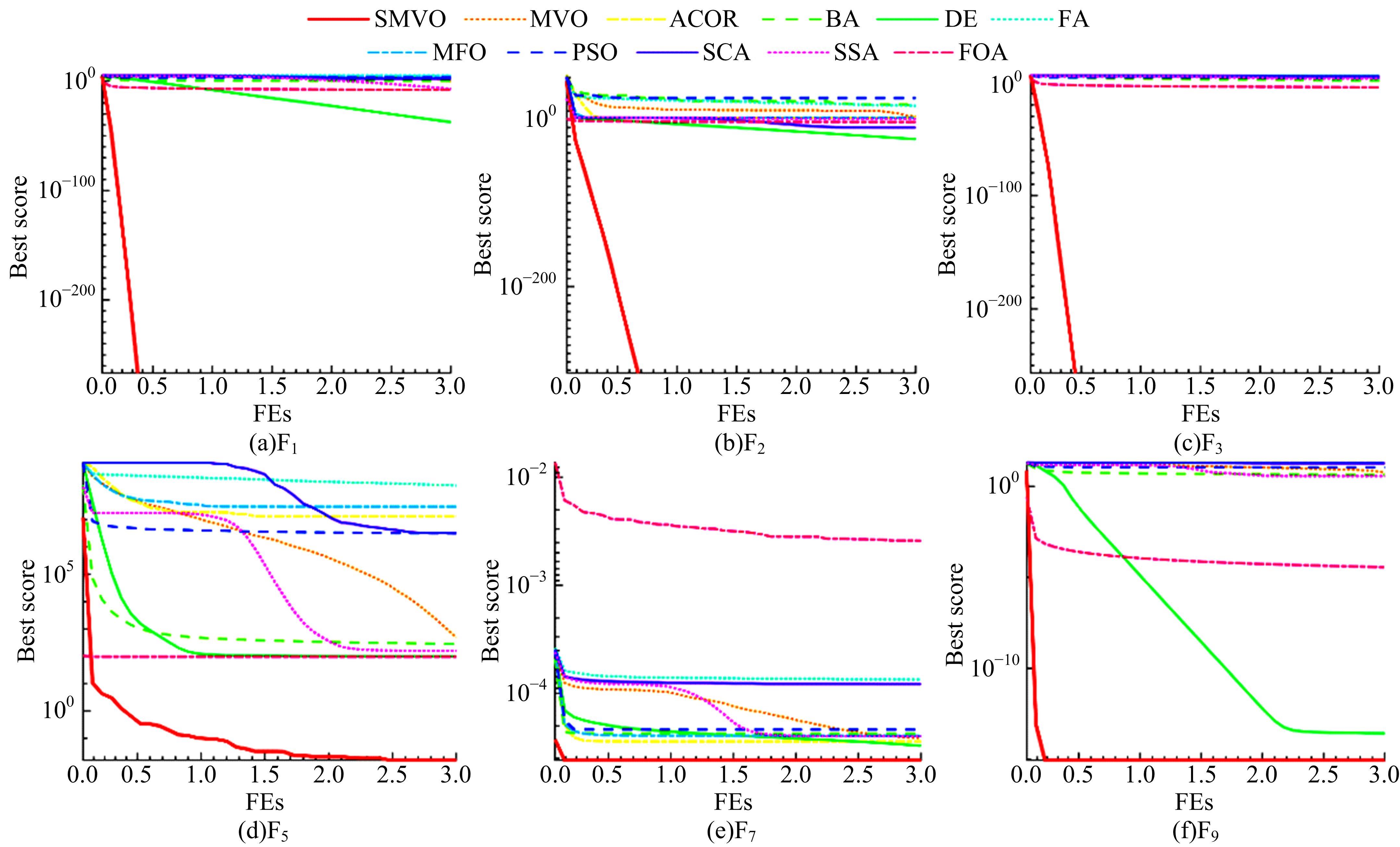
为提高多元宇宙优化算法求解实际问题的能力，提出了一种黏菌觅食的多元宇宙优化算法。该算法利用黏菌觅食行为在局部最优和全局最优之间寻求最优解。通过与其他10种同类算法在12个函数上的测试比较表明：本文算法收敛速度及解的质量优于其他算法，具有更好的求解能力和优化性能，可作为问题优化的有效工具。

关键词: 计算机应用, 细菌觅食行为, 多元宇宙优化算法, 函数优化

Abstract:

In order to improve the ability of multi-verse optimization algorithm to solve practical problems, a modified multi-verse optimization algorithm with slime mould foraging is proposed. The algorithm uses slime foraging behavior to further seek optimal solutions between local optimum and global optimum. By comparing with 10 other similar algorithms tested on 12 benchmark-functions, the results show that the convergence speed and solution quality of the proposed algorithm in this paper are better than other algorithms, with better solving ability and optimization performance, and can be used as an effective tool for problem optimization.

Key words: computer applications, slime mould foraging behavior, multi-verse optimization（MVO） algorithm, function optimization

中图分类号:

TP393

任丽莉,王志军,闫冬梅. 结合黏菌觅食行为的改进多元宇宙算法[J]. 吉林大学学报(工学版), 2021, 51(6): 2190-2197.

Li-li REN,Zhi-jun WANG,Dong-mei YAN. Improved multi⁃verse algorithm with combined slime mould foraging behavior[J]. Journal of Jilin University(Engineering and Technology Edition), 2021, 51(6): 2190-2197.

图/表 4

表 1

基准函数描述"

函数	函数公式	参数取值	最小值
F₁	$f 1 x = ∑ i = 1 n x i 2$		0
F₂	$f 2 x = x i + ∏ i = 1 n x i$		0
F₃	$f 3 x = ∑ i = 1 n ∑ j - 1 i x j 2$		0
F₄	$f 4 x = m a x i {x i, 1 ≤ i ≤ n}$		0
F₅	$f 5 x = ∑ i = 1 n - 1 [100 (x i + 1 - x i 2) 2 + (x i - 1) 2]$		0
F₆	$f 6 x = ∑ i = 1 n x i + 0.5 2$		0
F₇	$f 7 x = ∑ i = 1 n - x i s i n \| x i \|$		-418.9829×n
F₈	$f 8 x = ∑ i = 1 n [x i 2 - 10 c o s 2 π x i + 10]$	［-5.12，5.12］	0
F₉	$f 9 x = - 20 e x p - 0.2 1 n ∑ i = 1 n x i -$ $e x p 1 n ∑ i = 1 n c o s 2 π x i + 20 + e$		0
F₁₀	$f 10 x = 14000 ∑ i = 1 n x i 2 - ∏ i = 1 n c o s x i i + 1$		0
F₁₁	$f 11 x = π n 10 s i n a y 1 +$ $∑ i = 1 n - 1 (y i - 1) 2 [1 + 10 s i n 2 (π y i + 1)] +$ $???????????????? (y n - 1) 2 + ∑ i = 1 n μ (x i, 10,100,4)$ $y i = 1 + (x i + 1) / 4$ ； $μ x i, a, k, m = k x i - a m, ?????? x i > a 0, ?????? - a < x i < a k - x i - a m, ?????? x i < - a$		0
F₁₂	$f 12 x = 0.1 s i n 2 3 π x i +$ $∑ i = 1 n x i - 1 2 1 + s i n 2 3 π x i + 1 +$ $?????????? x n - 1) 2 1 + s i n 2 2 π x n +$ $∑ i = 1 n μ (x i, 5,100,4)$		0

表 1

表2

SMVO和10个同类算法的比较结果"

函数	指标	算法
函数	指标	SMVO	MVO	ACOR	BA	DE	FA	MFO	PSO	SCA	SSA	FOA
F₁	AVG	0.0000E+00	3.8821E-01	8.3333E+03	9.6820E-01	3.5921E-38	8.9258E+04	1.7885E+04	1.0215E+03	9.2607E+01	7.1331E-08	8.3400E-09
F₁	STD	0.0000E+00	5.7880E-02	7.4664E+03	5.6898E-01	2.3499E-38	4.2672E+03	1.6008E+04	5.5314E+01	2.0806E+02	8.6630E-09	2.4030E-11
F₂	AVG	0.0000E+00	6.8669E+03	9.6333E+01	9.4976E+13	3.0648E-24	1.3083E+16	1.4633E+02	3.7238E+25	1.0159E-10	6.5869E+00	9.1360E-04
F₂	STD	0.0000E+00	3.5845E+04	2.4280E+01	3.7080E+14	1.3807E-24	3.4100E+16	5.1427E+01	2.0365E+26	3.4747E-10	3.4193E+00	1.3357E-06
F₃	AVG	0.0000E+00	2.6883E+03	1.4986E+05	1.7049E+01	2.9061E+05	2.3464E+05	1.3382E+05	1.0788E+04	9.5811E+04	1.9569E+03	2.8263E-05
F₃	STD	0.0000E+00	4.0873E+02	2.8063E+04	2.2746E+01	1.8556E+04	1.9245E+04	6.3781E+04	1.7024E+03	2.6538E+04	8.4069E+02	6.8662E-08
F₄	AVG	0.0000E+00	1.2104E+01	9.6771E+01	3.3869E+01	5.5452E+00	9.2689E+01	9.3025E+01	9.9060E+00	6.9119E+01	2.2962E+01	9.1370E-06
F₄	STD	0.0000E+00	4.5201E+00	1.4074E+00	9.0360E+00	6.6624E-01	3.8012E+00	2.3997E+00	1.1529E+00	4.3507E+00	3.4007E+00	1.3417E-08
F₅	AVG	1.5835E-02	4.9426E+02	1.3349E+07	2.8592E+02	1.0187E+02	1.7606E+08	2.9936E+07	3.1949E+06	3.2992E+06	1.6356E+02	9.8000E+01
F₅	STD	3.7012E-02	6.9841E+02	3.6869E+07	3.5499E+02	1.9726E+01	1.5717E+07	5.3247E+07	3.7002E+05	4.5742E+06	8.3286E+01	9.0545E-05
F₆	AVG	9.0036E-04	3.9619E-01	1.0350E+04	1.1715E+00	0.0000E+00	8.9748E+04	1.8681E+04	1.0071E+03	2.4174E+02	6.9710E-08	2.5001E+01
F₆	STD	1.6295E-03	6.2888E-02	1.0695E+04	7.2217E-01	0.0000E+00	4.6417E+03	1.4721E+04	6.6866E+01	5.5760E+02	6.6761E-09	1.6127E-06
F₇	AVG	-4.1898 E+04	-2.6001 E+04	-2.7968 E+04	-2.3691 E+04	-3.0562 E+04	-7.4199 E+03	-2.4779 E+04	-2.1629 E+04	-8.2331 E+03	-2.5007 E+04	-3.8652 E+02
F₇	STD	2.2476E-03	1.1331E+03	9.8801E+02	1.3029E+03	3.4339E+03	3.3381E+02	3.2373E+03	2.6617E+03	5.2180E+02	1.4100E+03	1.0746E+02
F₈	AVG	0.0000E+00	5.5830E+02	8.1668E+02	1.1135E+03	4.5580E+02	1.1000E+03	6.1028E+02	1.5153E+03	1.1892E+02	1.9594E+02	1.6559E-06
F₈	STD	0.0000E+00	7.9842E+01	2.6996E+02	8.4706E+01	1.5662E+01	2.6471E+01	9.1932E+01	6.0336E+01	7.1792E+01	4.2158E+01	5.8328E-09
F₉	AVG	8.8818E-16	5.8807E+00	2.0469E+01	4.4138E+00	2.7060E-14	1.8817E+01	1.9839E+01	1.1143E+01	1.8607E+01	3.6859E+00	3.6561E-05
F₉	STD	0.0000E+00	7.6754E+00	3.4023E-01	4.2681E+00	2.7174E-15	1.3307E-01	2.6975E-01	1.9434E-01	5.9012E+00	7.5550E-01	5.4312E-08
F₁₀	AVG	0.0000E+00	4.3777E-01	1.0842E+02	1.8523E+01	0.0000E+00	8.0778E+02	1.5486E+02	1.2549E+00	2.3668E+00	2.6268E-03	2.1868E-10
F₁₀	STD	0.0000E+00	5.6867E-02	1.1457E+02	2.2898E+01	0.0000E+00	4.3289E+01	1.2573E+02	1.6028E-02	5.9518E+00	5.6705E-03	6.5896E-13
F₁₁	AVG	9.5530E-07	4.2929E+00	3.4150E+07	1.4669E+01	4.7116E-33	2.4717E+08	8.6413E+07	1.9446E+01	6.7238E+06	1.0379E+01	1.3254E+00
F₁₁	STD	1.4455E-06	1.2730E+00	8.8505E+07	3.3454E+00	1.3918E-48	3.6377E+07	1.3942E+08	6.6756E+00	1.0208E+07	2.4541E+00	4.7128E-08

表2

图1

图2

参考文献 27

1	王伟, 何东之. 基于非线性和遗传变异的灰狼优化算法[J]. 合肥工业大学学报: 自然科学版, 2021, 44(2): 199-205.
	Wang Wei, He Dong-zhi. Gray wolf optimization algorithm based on nonlinearity and genetic variation[J]. Journal of Hefei University of Technology (Natural Science Edition), 2021, 44(2): 199-205.
2	Socha K, Dorigo M. Ant colony optimization for continuous domains[J]. European Journal of Operational Research, 2008, 185(3): 1155-1173.
3	Yang X S. A new metaheuristic bat-inspired algorithm[C]∥Nature inspired cooperative strategies for optimization (NICSO 2010), Springer, , HeidelbergBerlin, 2010: 65-74.
4	Storn R, Price K. Differential evolution—a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization, 1997, 11(4): 341-359.
5	Yang X S. Firefly algorithms for multimodal optimization[C]∥International Symposium on Stochastic Algorithms, Springer, Berlin, Heidelberg, 2009: 169-178.
6	Mirjalili S. Moth-flame optimization algorithm: a novel nature-inspired heuristic paradigm[J]. Knowledge-Based Systems, 2015, 89: 228-249.
7	Poli R, Kennedy J, Blackwell T. Particle swarm optimization[J].Swarm Intelligence, 2007, 1(1): 33-57.
8	Mirjalili S. SCA: a sine cosine algorithm for solving optimization problems[J]. Knowledge-based Systems, 2016, 96: 120-133.
9	Mirjalili S, Gandomi A H, Mirjalili S Z, et al. Salp swarm algorithm: a bio-inspired optimizer for engineering design problems[J]. Advances in Engineering Software, 2017, 114: 163-191.
10	Pan W T. A new fruit fly optimization algorithm: taking the financial distress model as an example[J]. Knowledge-Based Systems, 2012, 26: 69-74.
11	Mirjalili S, Mirjalili S M, Hatamlou A. Multi-verse optimizer: a nature-inspired algorithm for global optimization[J]. Neural Computing and Applications, 2016, 27(2): 495-513.
12	熊保玉. 基于改进多元宇宙算法的零件平面度测量研究[J]. 光电子·激光, 2021, 32(3): 251-256.
	Xiong Bao-yu. Research on part flatness measurement based on improved multiverse algorithm[J]. Journal of Optoelectronics·Laser, 2021, 32(3): 251-256.
13	Yang X H, Chen W K, Li A Y, et al. A Hybrid machine‐learning method for oil‐immersed power transformer fault diagnosis[J]. IEEJ Transactions on Electrical and Electronic Engineering, 2020, 15(4): 501-507.
14	Zhu L, Lin J, Wang Z J. A discrete oppositional multi-verse optimization algorithm for multi-skill resource constrained project scheduling problem[J]. Applied Soft Computing, 2019, 85: No.105805.
15	Yildiz A R, Mirjalili S, Sait S, et al. The Harris hawks, grasshopper and multi-verse optimization algorithms for the selection of optimal machining parameters in manufacturing operations[J]. Materials Testing, 2019, 61(8): 725-733.
16	Singh A, Suhag S. Frequency regulation in an AC microgrid interconnected with thermal system employing multiverse-optimised fractional order-PID controller[J]. International Journal of Sustainable Energy, 2020, 39(3): 250-262.
17	Lin J, Zhu L, Wang Z J. A hybrid multi-verse optimization for the fuzzy flexible job-shop scheduling problem[J]. Computers & Industrial Engineering, 2019, 127: 1089-1100.
18	Li L L, Wen S Y, Wang C S, et al. Renewable energy prediction: a novel short-term prediction model of photovoltaic output power[J]. Journal of Cleaner Production, 2019, 228: 359-375.
19	Geng K F, Ye C M, Cao L, et al. Multi-objective reentrant hybrid flowshop scheduling with machines turning on and off control strategy using improved multi-verse optimizer algorithm[J]. Mathematical Problems in Engineering, 2019, 2019: 1-18.
20	Chauhan U, Rani A, Kumar B, et al. A multi verse optimization based MPPT controller for drift avoidance in solar system[J]. Journal of Intelligent & Fuzzy Systems, 2019, 36(3): 2175-2184.
21	Buch H, Trivedi I N. On the efficiency of metaheuristics for solving the optimal power flow[J]. Neural Computing and Applications, 2019, 31(9): 5609-5627.
22	Al-qaness M A A, Elaziz M A, Ewees A A, et al. A modified adaptive neuro-fuzzy inference system using multi-verse optimizer algorithm for oil consumption forecasting[J]. Electronics, 2019, 8(10): 1071.
23	Liu Xiao-long. Application of improved multiverse algorithm to large scale optimization problems[J]. Journal of Electronics & Information Technology, 2019, 41(7): 1666-1673.
24	Ewees A A, Abd El Aziz M, Hassanien A E. Chaotic multi-verse optimizer-based feature selection[J]. Neural Computing and Applications, 2019, 31(4): 991-1006.
25	Li S M, Chen H L, Wang M J. et al. Slime mould algorithm: A new method for stochastic optimization[J]. Future Generation Computer Systems, 2020, 111: 300-323.
26	García S, Fernández A, Luengo J, et al. Advanced nonparametric tests for multiple comparisons in the design of experiments in computational intelligence and data mining: Experimental analysis of power[J]. Information Sciences, 2010, 180(10): 2044-2064.
27	Derrac J, García S, Molina D, et al. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms[J]. Swarm and Evolutionary Computation, 2011, 1(1): 3-18.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

[1]	赵宏伟,霍东升,王洁,李晓宁. 基于显著性检测的害虫图像分类[J]. 吉林大学学报(工学版), 2021, 51(6): 2174-2181.
[2]	孙东明,胡亮,邢永恒,王峰. 基于文本融合的物联网触发动作编程模式服务推荐方法[J]. 吉林大学学报(工学版), 2021, 51(6): 2182-2189.
[3]	王生生,陈境宇,卢奕南. 基于联邦学习和区块链的新冠肺炎胸部CT图像分割[J]. 吉林大学学报(工学版), 2021, 51(6): 2164-2173.
[4]	林俊聪,雷钧,陈萌,郭诗辉,高星,廖明宏. 基于电影视觉特性的动态多目标实时相机规划[J]. 吉林大学学报(工学版), 2021, 51(6): 2154-2163.
[5]	姚引娣,贺军瑾,李杨莉,谢荡远,李英. 自构建改进型鲸鱼优化BP神经网络的ET₀模拟计算[J]. 吉林大学学报(工学版), 2021, 51(5): 1798-1807.
[6]	赵宏伟,张子健,李蛟,张媛,胡黄水,臧雪柏. 基于查询树的双向分段防碰撞算法[J]. 吉林大学学报(工学版), 2021, 51(5): 1830-1837.
[7]	张萌谡,刘春天,李希今,黄永平. 基于K⁃means聚类算法的绩效考核模糊综合评价系统设计[J]. 吉林大学学报(工学版), 2021, 51(5): 1851-1856.
[8]	曹洁,屈雪,李晓旭. 基于滑动特征向量的小样本图像分类方法[J]. 吉林大学学报(工学版), 2021, 51(5): 1785-1791.
[9]	杨勇,陈强,曲福恒,刘俊杰,张磊. 基于模拟划分的SP⁃k⁃means-+算法[J]. 吉林大学学报(工学版), 2021, 51(5): 1808-1816.
[10]	孙小雪,钟辉,陈海鹏. 基于决策树分类技术的学生考试成绩统计分析系统[J]. 吉林大学学报(工学版), 2021, 51(5): 1866-1872.
[11]	王春波,底晓强. 基于标签分类的云数据完整性验证审计方案[J]. 吉林大学学报(工学版), 2021, 51(4): 1364-1369.
[12]	欧阳丹彤,刘扬,刘杰. 故障响应指导下基于测试集的故障诊断方法[J]. 吉林大学学报(工学版), 2021, 51(3): 1017-1025.
[13]	钱榕,张茹,张克君,金鑫,葛诗靓,江晟. 融合全局和局部特征的胶囊图神经网络[J]. 吉林大学学报(工学版), 2021, 51(3): 1048-1054.
[14]	朱小龙,谢忠. 基于机器学习的地理空间数据抽取算法[J]. 吉林大学学报(工学版), 2021, 51(3): 1011-1016.
[15]	孙宝凤,任欣欣,郑再思,李国一. 考虑工人负荷的多目标流水车间优化调度[J]. 吉林大学学报(工学版), 2021, 51(3): 900-909.