新的6⁃PSS型并联机构正向运动学求解方法

doi:10.13229/j.cnki.jdxbgxb20180636

摘要/Abstract

摘要：

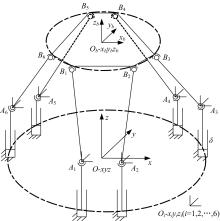
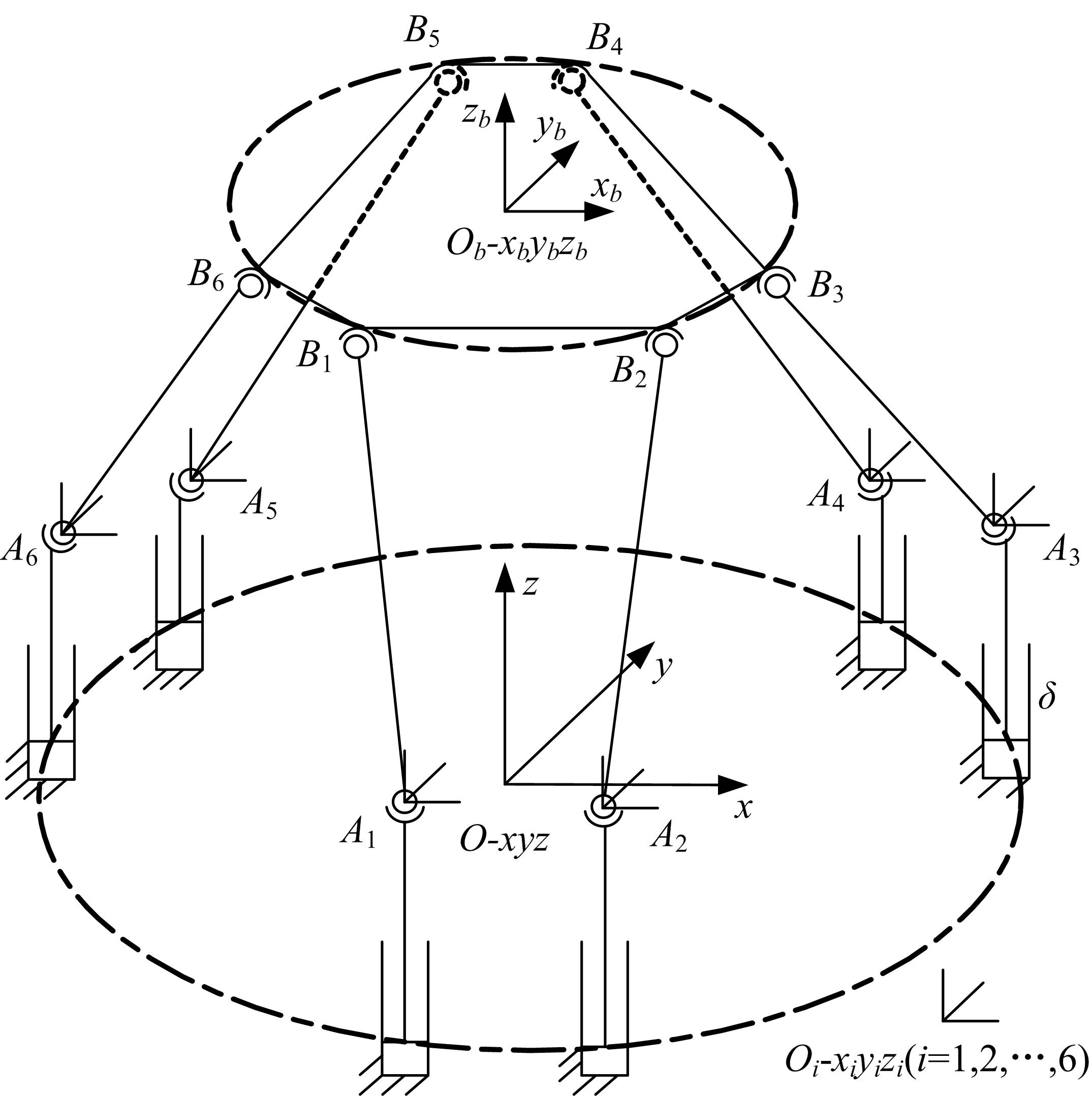
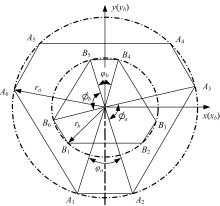
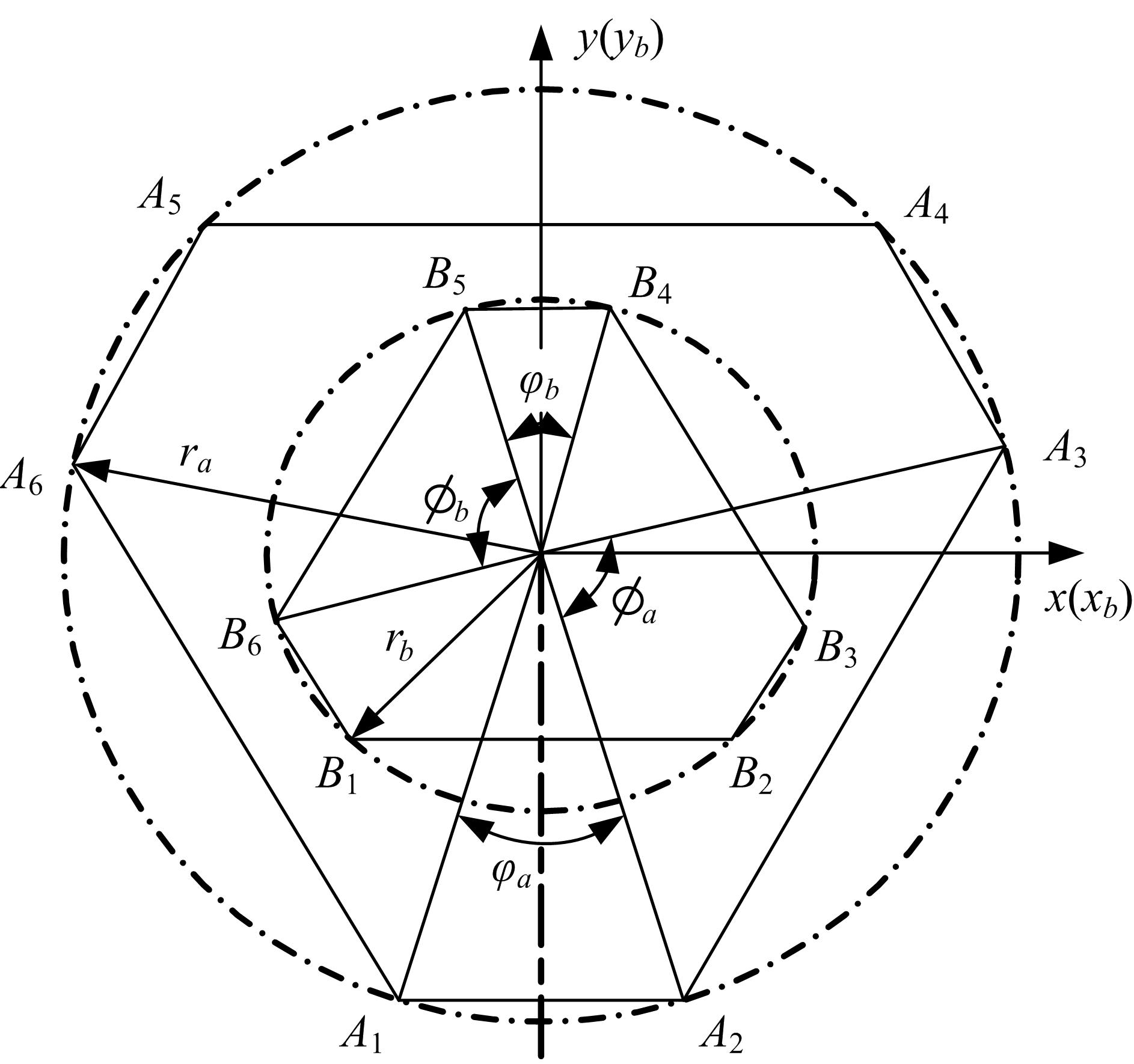
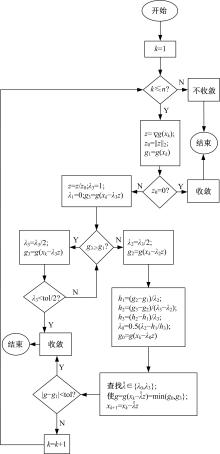
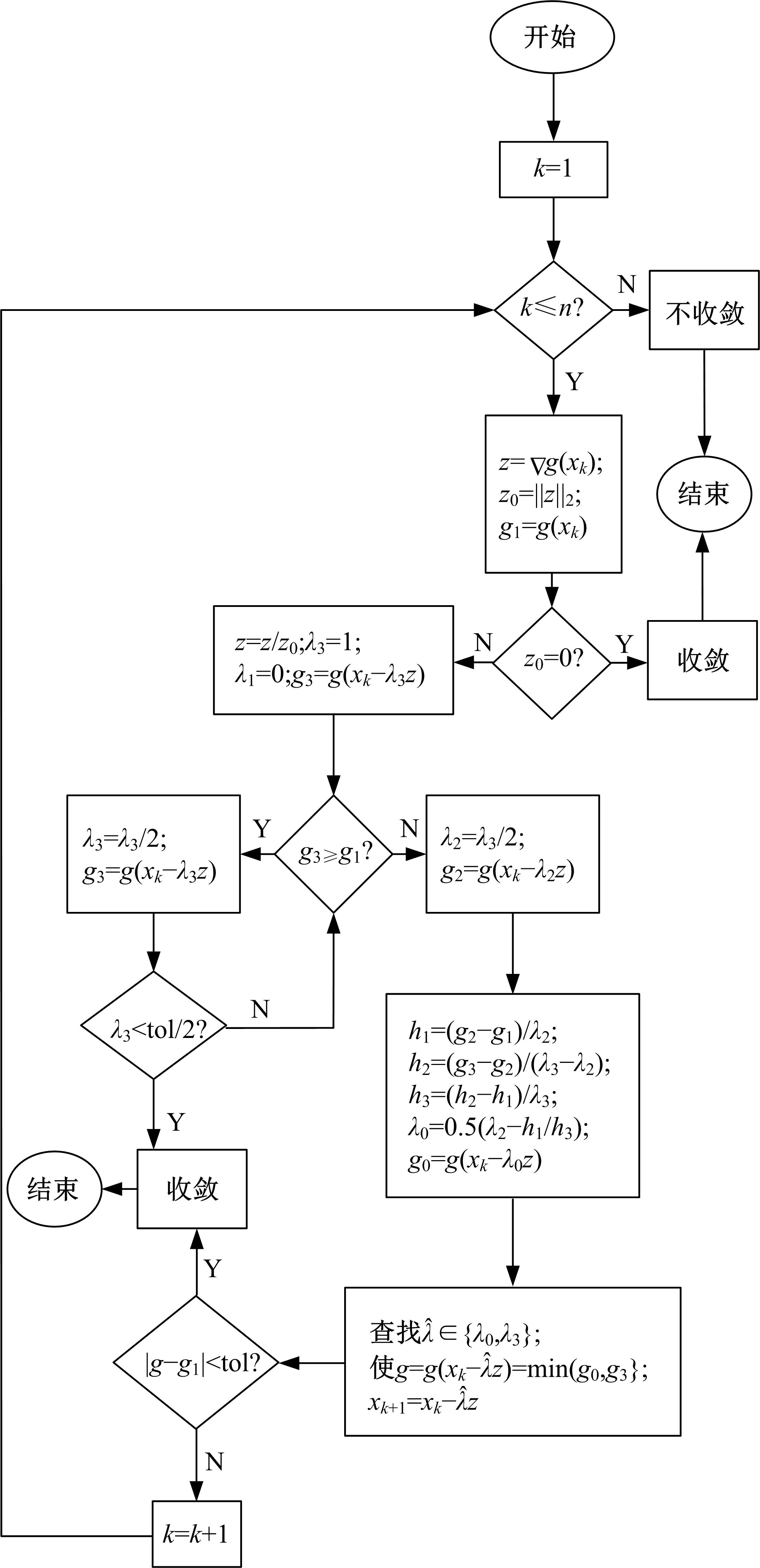
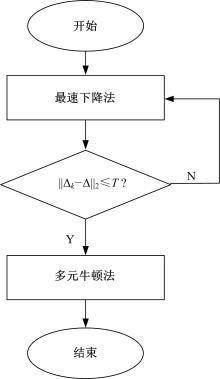
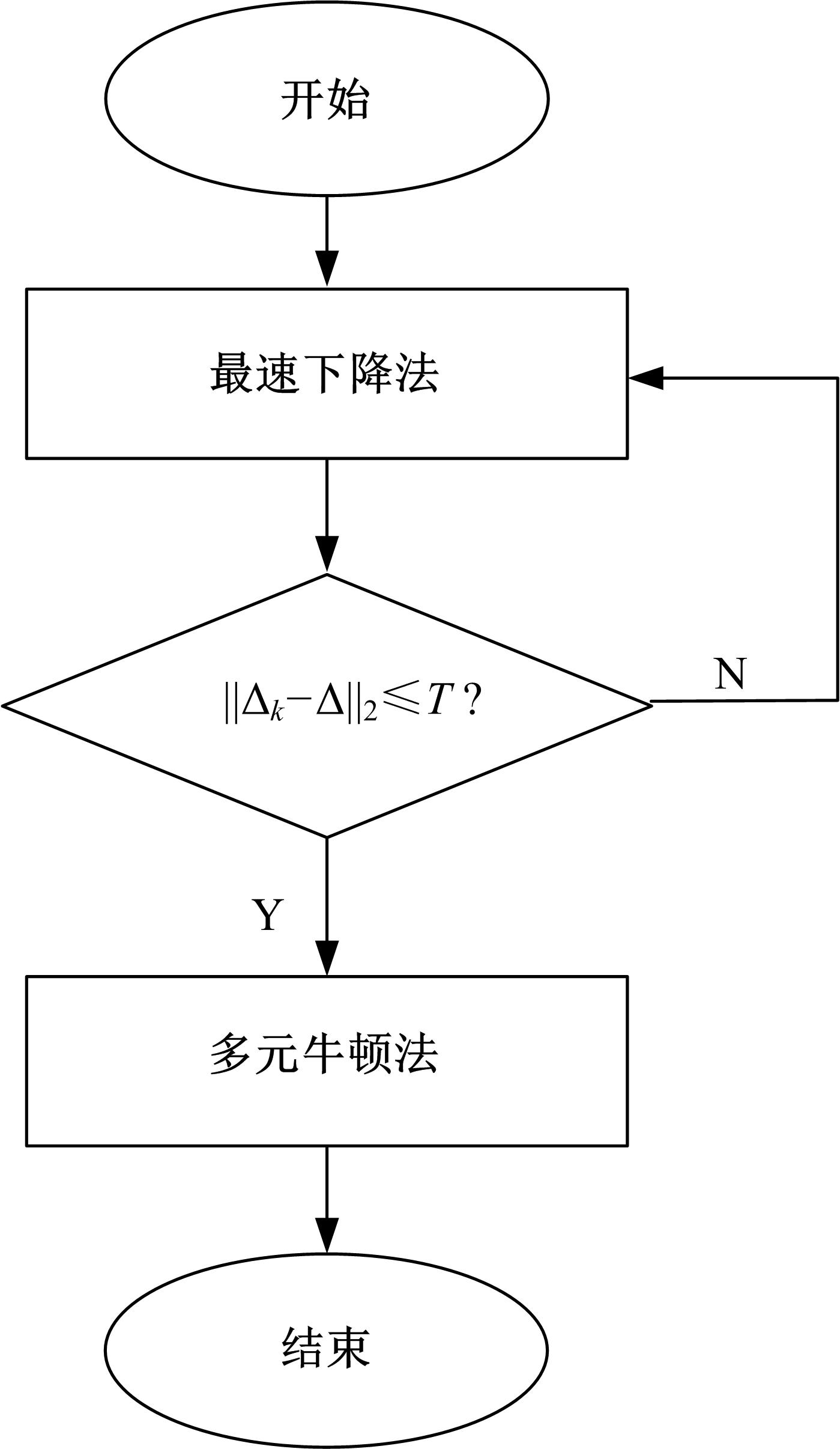
针对6-PSS型并联机构，通过研究其正向运动学，利用各支链铰点在动坐标系、静坐标系和滑块铰点坐标系3种坐标系下的位置关系，推导出6-PSS型并联机构的运动学模型，得到一种简明的运动学正向求解方法。在此基础上，提出了基于多元牛顿法和最速下降法的组合数值方法，并运用数值分析理论和计算机机器算数思想，最大限度提高收敛速度和减少单步迭代计算量。最后，编制了机构运动学的正向求解程序，进行了数值仿真，结果表明：改进的组合数值方法不仅可以更加快速地收敛到真实解，还能降低对初始估计值的依赖，扩大收敛范围，可以有效应用于该型并联机器人系统。

关键词: 机械设计, 6-PSS型并联机构, 运动学正解, 多元牛顿法, 最速下降法, 组合数值方法

Abstract:

Through the research of 6-PSS parallel manipulator, this paper developed the kinematics model based on the relationship between spherical joints' spatial positions in three kinds of coordinate systems, which respectively are the global coordinate system, the local coordinate system and the hinge-point coordinate systems fixed on sliding blocks. A composed numerical method based on multivariate Newton's method and the steepest descent method was proposed. The theories of numerical analysis and machine computation were used to improve the convergence speed and decrease the amount of operations in a single-step iterative process. Finally, the forward kinematics solution program was written for the numerical simulation. The results show that the improved composed numerical method can not only decrease the computational time and converge to the solution accurately, but also reduce the dependence on the initial estimate and expand the convergence range. This method can be effectively applied in robot system based on 6-PSS parallel manipulator.

Key words: mechanical design, 6-PSS parallel manipulator, forward kinematics solution, multivariate Newton's method, the steepest descent method, composed numerical method

中图分类号:

TH113

谢志江,王昆,皮阳军,吴小勇,郭映位. 新的6⁃PSS型并联机构正向运动学求解方法[J]. 吉林大学学报(工学版), 2019, 49(6): 1977-1985.

Zhi-jiang XIE,Kun WANG,Yang-jun PI,Xiao-yong WU,Ying-wei GUO. Novel method for forward kinematics of 6⁃PSSparallel manipulator[J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(6): 1977-1985.

图/表 6

图1

图2

图3

图4

表1

6?PSS机器人结构参数表"

$l$ /mm	$r a$ /mm	$r b$ /mm	$? a$	$φ a$	$? b$	$φ b$
1 000	500	250	$π / 2$	$π / 6$	$π / 2$	$π / 6$

表1

表2

部分点的仿真结果统计表"

序号	输入量 $Δ i (i = 1,2, …, 6)$ /mm	最速下降法迭代次数	多元牛顿法迭代次数	组合方法总时间/s	组合方法输出 $α, β, γ, x c, y c, z c$ $/ (r a d ? ? ? ? ? ? o r ? ? ? ? ? ? ? m m)$	单独牛顿法迭代次数	单独牛顿法总时间 /s	单独牛顿法输出 $α, β, γ, x c, y c, z c$ $/ (r a d ? ? ? ? ? ? o r ? ? ? ? ? ? ? m m)$
1	-52.978，75.410， 126.710，47.602， -12.726，-35.234	无	无	无	无	5	0.001 74	0.100 000，0.199 999， 0.299 998，60.001 5， 39.998 6，20.000 0
2	-42.318，194.962， 332.980，168.590， 27.590，60.318	1	5	0.001 83	0.400 008，0.299 999， 0.700 001，199.999 5， 119.999 3，79.999 994	6	0.002 02	0.400 008，0.299 999， 0.700 001，199.999 5， 119.999 3，80.000 0
3	-14.826，222.002， 319.326，244.300， 127.828，179.708	2	5	0.001 92	0.700 001，0.400 001， 0.600 001，139.999 6， 200.001 5，119.999 4	7	0.002 11	0.700 001，0.400 001， 0.600 001，139.999 6， 200.001 5，119.999 4
4	-80.150，187.780， 310.226，160.274， 60.206，17.606	2	5	0.001 85	0.400 003，0.499 998， 0.699 999，100.000 4， 139.999 7，80.000 0	7	0.002 13	0.400 003，0.499 998， 0.699 999，100.000 4， 139.999 7，80.000 0
5	53.542，296.142， 475.294，401.766， 292.904，215.102	2	5	0.001 89	0.400 000，0.599 999， 0.500 003，159.999 776， 200.001 1，239.999 9	7	0.002 24	0.400 000，0.599 999， 0.500 003，159.999 8， 200.001 1，239.999 9
6	-46.182，212.540， 402.078，338.712， 184.406，140.414	2	5	0.001 93	0.599 998，0.600 002， 0.600 002，199.9998， 200.000 8，139.9996	7	0.002 16	0.599 998，0.600 002 0.600 002，199.999 8 200.000 8，139.999 6
7	-33.282，27.601， 171.838，517.644， 476.066，344.207	2	5	0.002 06	0.600 006，0.600 001 -0.499 998，209.998 5 240.000 9，149.999 8	不收敛	无	无
8	530.796，724.202， 152.260，-137.024， 186.516，727.426	6	5	0.002 95	0.799 996，-0.700 001， 0.999 999，-400.000 2， 250.001 0，120.000 0	不收敛	无	无
9	183.230，510.146， 951.193，822.089， 521.558，443.330	10	7	0.004 68	0.799 996，0.800 002， 0.999 998，400.000 4， 250.000 0，400.000 0	不收敛	无	无
10	-167.026，131.332， 533.602，835.502， 445.204，149.052	10	7	0.004 86	1.499 985，1.199 999， 0.999 989，360.001 4， 319.999 4，100.000 0	不收敛	无	无

表2

参考文献

1	Merlet J P . Parallel Robots[M]. The Netherlands: Springer, 2006.
2	程世利, 吴洪涛, 姚裕,等 . 6-SPS并联机构运动学正解的一种解析化方法[J]. 机械工程学报, 2010, 46(9): 26-31.
2	Cheng Shi-li , Wu Hong-tao , Yao Yu , et al . An analytical method for the forward kinematics analysis of 6-SPS parallel mechanisms[J]. Journal of Mechanical Engineering, 2010, 46(9): 26-31.
3	Innocenti C , Parenti-Castelli V . Closed-form direct position analysis of a 5-5 parallel mechanism[J]. Journal of Mechanical Design, 1993, 115(3): 515-521.
4	Boyd D W . Non-convergence in Bairstow's method[J]. SIAM Journal on Numerical Analysis, 1977, 14(3): 571-574.
5	Mcnamee J M , Pan V Y . Jenkins–Traub, Minimization, and Bairstow methods—chapter 11[J]. Studies in Computational Mathematics, 2013, 16: 461-526.
6	李鹭扬 . 6-SPS型并联机床若干关键理论研究[D].南京：南京航空航天大学机电学院, 2007.
6	Li Lu-yang . Research on some key theoretical issues of 6-SPS parallel kinematic machines[D]. Nanjing: College of Mechanical and Electrical Engineering, Nanjing University of Aeronautics and Astronautics, 2007.
7	Markley F L , Cheng Y , Crassidis J L , et al . Averaging quaternions[J]. Journal of Guidance, Control, and Dynamics, 2007, 30(4): 1193-1197.
8	Hanson A J . Visualizing Quaternions[M]. San Francisco:Morgan Kaufmann Publishers Inc., 2006.
9	Raghavan M . The Stewart platform of general geometry has 40 configurations[J]. Journal of Mechanical Design, 1993, 115(2): 277-282.
10	?ika Z , Ko?andrle V , Stejskal V . An investigation of properties of the forward displacement analysis of the generalized Stewart platform by means of general optimization methods[J]. Mechanism and Machine Theory, 1998, 33(3): 245-253.
11	Didrit O , Petitot M , Walter E . Guaranteed solution of direct kinematic problems for general configurations of parallel manipulators[J]. IEEE Transactions on Robotics and Automation, 1998, 14(2): 259-266.
12	Kang J Y , Kim D H , Lee K I . Robust estimator design for forward kinematics solution of a Stewart platform[J]. Journal of Robotic Systems, 1998, 15(1): 29-42.
13	Zhao Xing-hua , Peng Shang-xian . Direct displacement analysis of parallel manipulators[J]. Journal of Robotic Systems, 2000, 17(6): 341-345.
14	Der-Ming K . Direct displacement analysis of a Stewart platform mechanism[J]. Mechanism and Machine Theory, 1999, 34(3): 453-465.
15	王启明, 苏建, 张兰, 等 . 基于L-M算法的正交Stewart平台位姿正解的初值补偿[J]. 吉林大学学报:工学版, 2017, 47(1): 97-104.
15	Wang Qi-ming , Su Jian , Zhang Lan , et al . Forward kinematics of orthogonal Stewart platform based on L-M algorithm[J]. Journal of Jilin University (Engineering and Technology Edition), 2017, 47(1): 97-104.
16	孙小勇, 郑彬, 鲍捷, 等 . 高速6-PSS并联机器人参数优化设计[J]. 农业机械学报, 2015, 46(5): 372-378.
16	Sun Xiao-yong , Zheng Bin , Bao Jie , et al . Parameter optimization design of high-speed 6-PSS parallel robot [J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(5): 372-378.
17	谢志江,等 . 测量空间六自由度运动的滑块式并联机构[P].中国:CN 102645170A, 2014-07-05.
18	Sauer T . Numerical Analysis[M]. 2nd ed. Boston, USA: Pearson Education, 2011.
19	Burden R L , Faires J D . Numerical Analysis[M]. 9th ed.Boston, USA: Brooks Cole, 2010.
20	Boyd S , Vandenberghe L . Convex Optimization [M]. London, UK: Cambridge University Press, 2004.
21	Nocedal J , Wright S J . Numerical Optimization[M]. 2nd ed.New York, USA: Springer-Verlag, 2006.
22	Angeles J . Is there a characteristic length of a rigid-body displacement?[J]. Mechanism & Machine Theory, 2006, 41(8):884-896.
23	Garrido M , K?llstr?m P , Kumm M , et al . CORDIC II: a new improved CORDIC algorithm[J]. IEEE Transactions on Circuits & Systems II Express Briefs, 2016, 63(2):186-190.
24	Tajima S , Ohara K , Terui A . An extension and efficient calculation of the Horner's rule for matrices[C]∥International Congress on Mathematical Software, Heidelberg, Germany, 2014: 346-351.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

[1]	贾富淳,孟宪皆,雷雨龙. 基于多目标遗传算法的二自由度动力吸振器优化设计[J]. 吉林大学学报(工学版), 2019, 49(6): 1969-1976.
[2]	曹恩国,刘坤,吉硕,孙震源,徐洪伟,骆星吉. 减重站起康复训练系统机械结构设计与优化[J]. 吉林大学学报(工学版), 2019, 49(5): 1558-1566.
[3]	李俊烨,刘洋,卢慧,孟文卿,杨兆军,张心明. 基于分子动力学的磨粒微切削单晶铁数值分析[J]. 吉林大学学报(工学版), 2019, 49(5): 1567-1574.
[4]	张艳芹,冯雅楠,孔鹏睿,于晓东,孔祥滨. 基于热油携带的静压支承油膜温度场及试验[J]. 吉林大学学报(工学版), 2019, 49(4): 1203-1211.
[5]	杨成,赵永胜,刘志峰,蔡力钢. 基于多尺度理论的栓接结合部动力学建模[J]. 吉林大学学报(工学版), 2019, 49(4): 1212-1220.
[6]	刘坤,吉硕,孙震源,徐洪伟,刘勇,赵静霞. 多功能坐站辅助型如厕轮椅机械结构设计与优化[J]. 吉林大学学报(工学版), 2019, 49(3): 872-880.
[7]	王兴野,张进秋,李国强,彭志召. 惯性质量对齿轮齿条式作动器阻尼特性的影响[J]. 吉林大学学报(工学版), 2019, 49(3): 881-887.
[8]	王家序,倪小康,韩彦峰,向果,肖科. 轴向往复运动下微槽轴承混合润滑数值模型[J]. 吉林大学学报(工学版), 2019, 49(3): 888-896.
[9]	毕秋实,王国强,黄婷婷,毛瑞,鲁艳鹏. 基于DEM-FEM耦合的双齿辊破碎机辊齿强度分析[J]. 吉林大学学报(工学版), 2018, 48(6): 1770-1776.
[10]	朱伟,王传伟,顾开荣,沈惠平,许可,汪源. 一种新型张拉整体并联机构刚度及动力学分析[J]. 吉林大学学报(工学版), 2018, 48(6): 1777-1786.
[11]	刘建芳, 王记波, 刘国君, 李新波, 梁实海, 杨志刚. 基于PMMA内嵌三维流道的压电驱动微混合器[J]. 吉林大学学报(工学版), 2018, 48(5): 1500-1507.
[12]	毛宇泽, 王黎钦. 鼠笼支撑一体化结构对薄壁球轴承承载性能的影响[J]. 吉林大学学报(工学版), 2018, 48(5): 1508-1514.
[13]	王涛, 伞晓刚, 高世杰, 王惠先, 王晶, 倪迎雪. 光电跟踪转台垂直轴系动态特性[J]. 吉林大学学报(工学版), 2018, 48(4): 1099-1105.
[14]	刘坤, 刘勇, 闫建超, 吉硕, 孙震源, 徐洪伟. 基于体外传感检测的人体站起动力学分析[J]. 吉林大学学报(工学版), 2018, 48(4): 1140-1146.
[15]	吉野辰萌, 樊璐璐, 闫磊, 徐涛, 林烨, 郭桂凯. 基于MBNWS算法的假人胸部结构多目标优化设计[J]. 吉林大学学报(工学版), 2018, 48(4): 1133-1139.