吉林大学学报(工学版) ›› 2022, Vol. 52 ›› Issue (11): 2644-2652.doi: 10.13229/j.cnki.jdxbgxb20210393
• 交通运输工程·土木工程 • 上一篇
不同吊杆形式悬索桥人致振动分析及舒适度评价
张彦玲1,2( ),王灿1,2,张旭1,2,王昂洋3,李运生1,2(
),王灿1,2,张旭1,2,王昂洋3,李运生1,2( )
)
- 1.石家庄铁道大学 土木工程学院,石家庄 050043
2.石家庄铁道大学 道路与铁道工程安全保障省部共建教育部重点实验室,石家庄 050043
3.国网河北省电力有限公司 沧州市供电分公司,河北 沧州 061000
Human⁃induced vibration analysis and pedestrian comfort evaluation for suspension footbridge with different hunger systems
Yan-ling ZHANG1,2( ),Can WANG1,2,Xu ZHANG1,2,Ang-yang WANG3,Yun-sheng LI1,2(
),Can WANG1,2,Xu ZHANG1,2,Ang-yang WANG3,Yun-sheng LI1,2( )
)
- 1.School of Civil Engineering,Shijiazhuang Tiedao University,Shijiazhuang 050043,China
2.Key Laboratory of Roads and Railway Engineering Safety Control of Ministry of Education,Shijiazhuang Tiedao University,Shijiazhuang 050043,China
3.Cangzhou Power Supply Branch of State Grid Hebei Electric Power Co. ,Ltd. ,Cangzhou 061000,China
摘要:
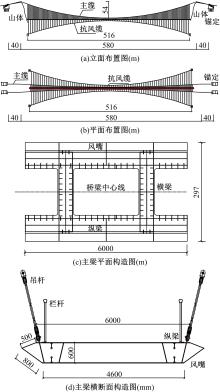
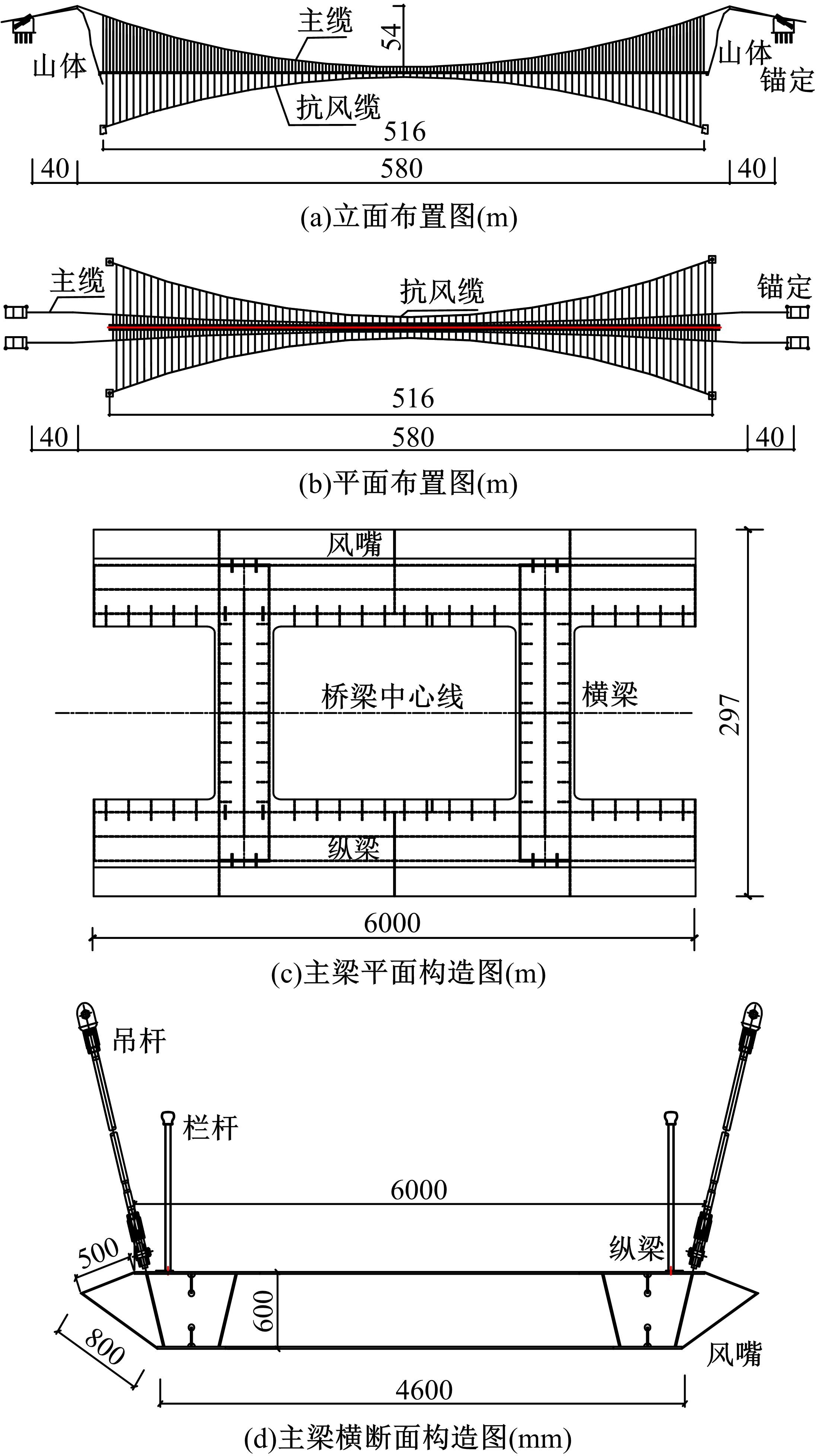
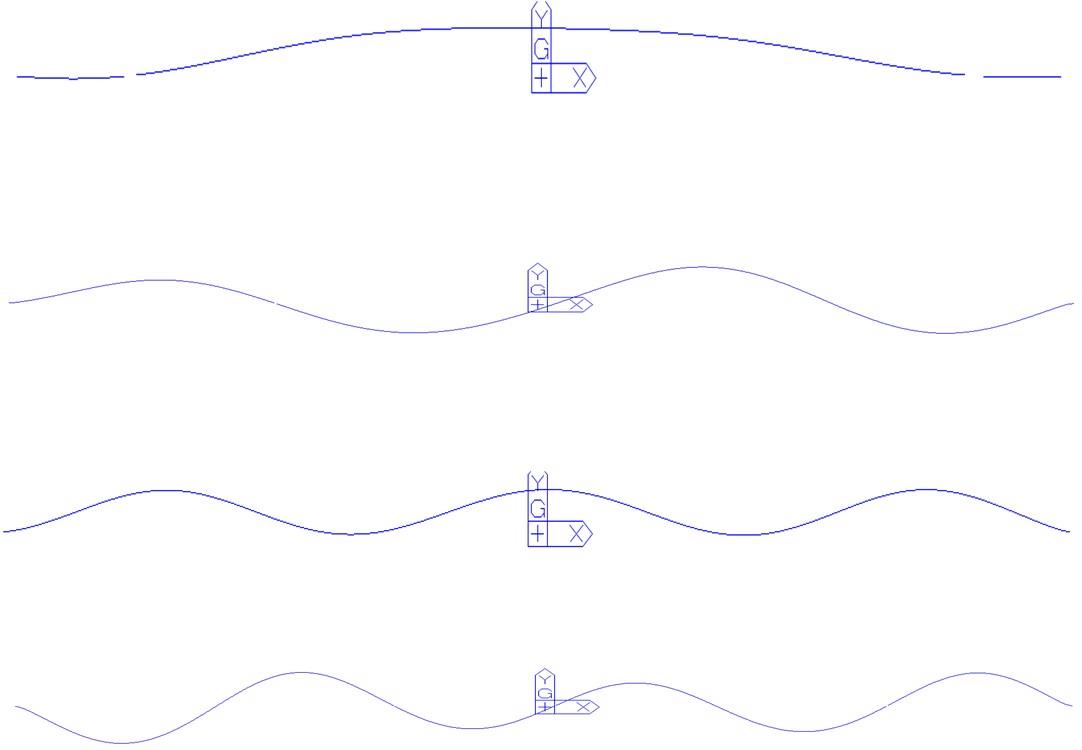
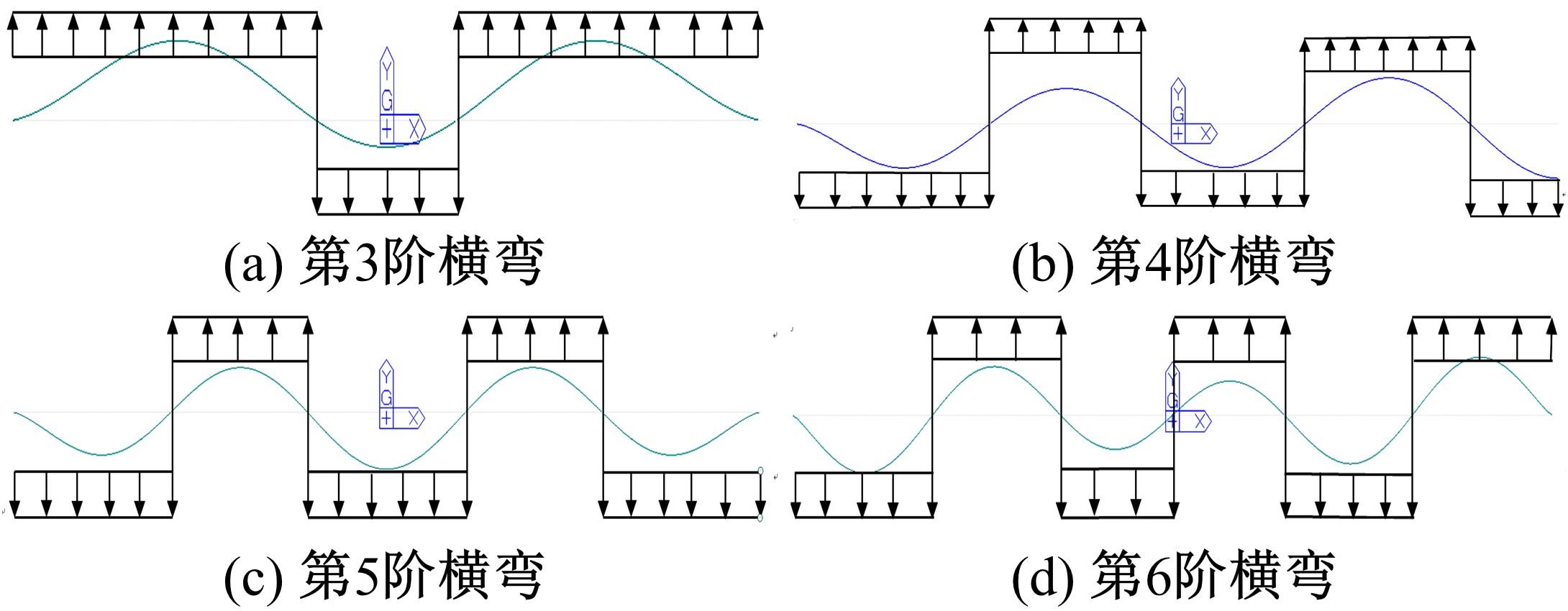
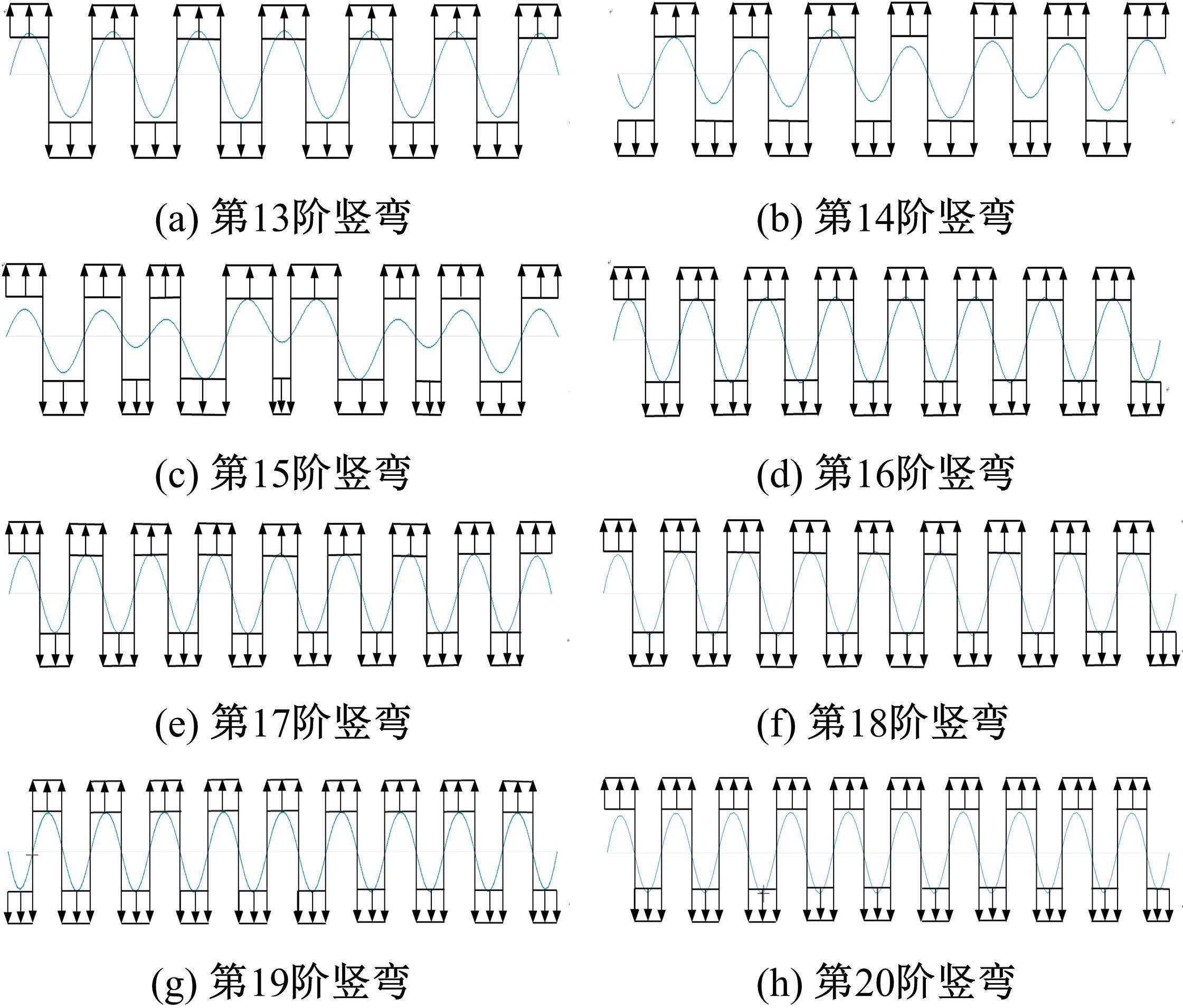
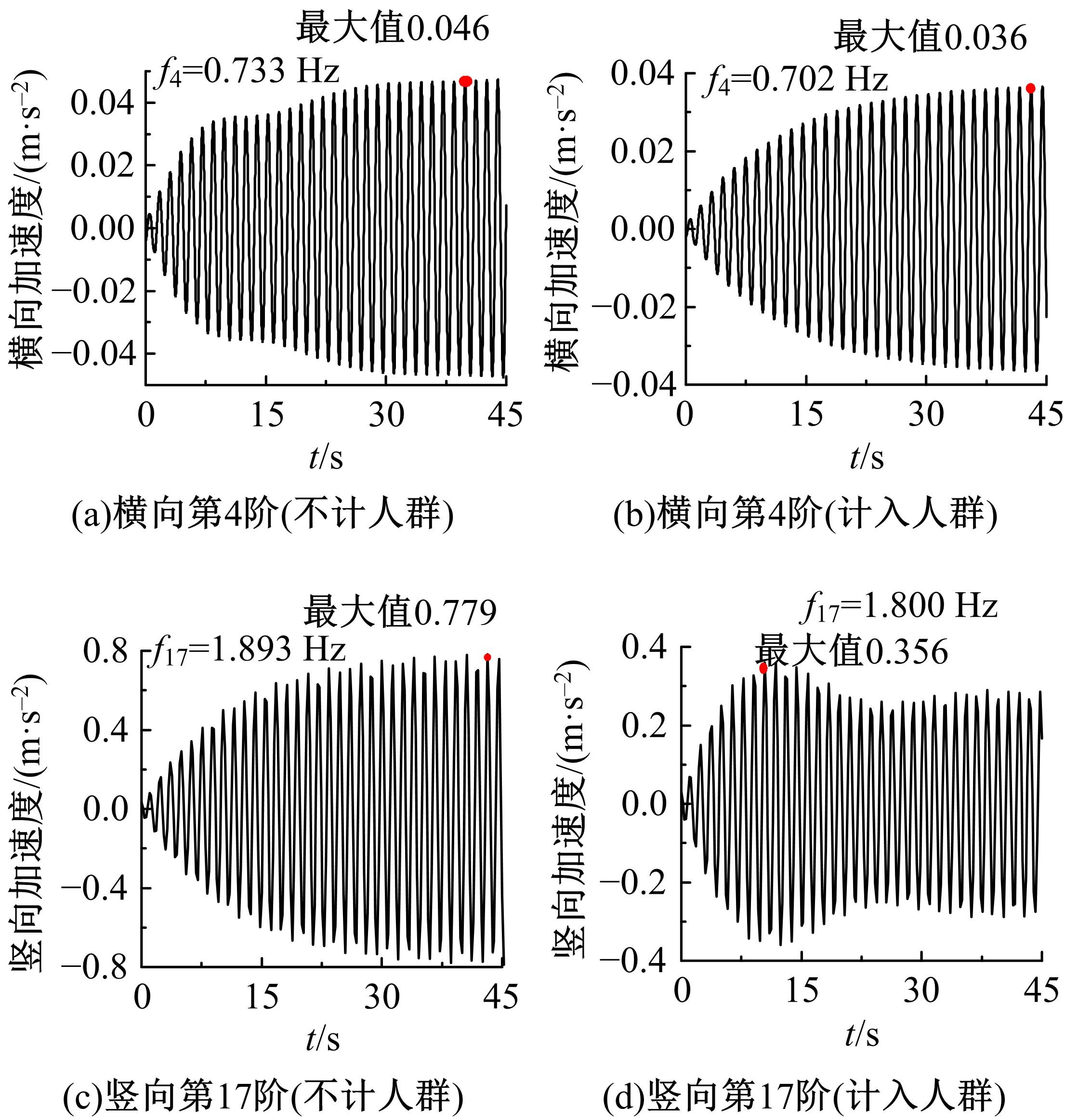
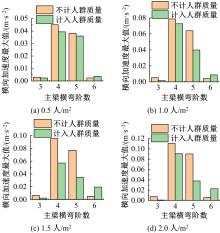
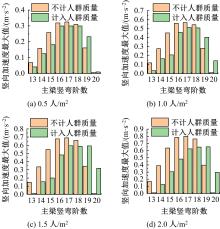
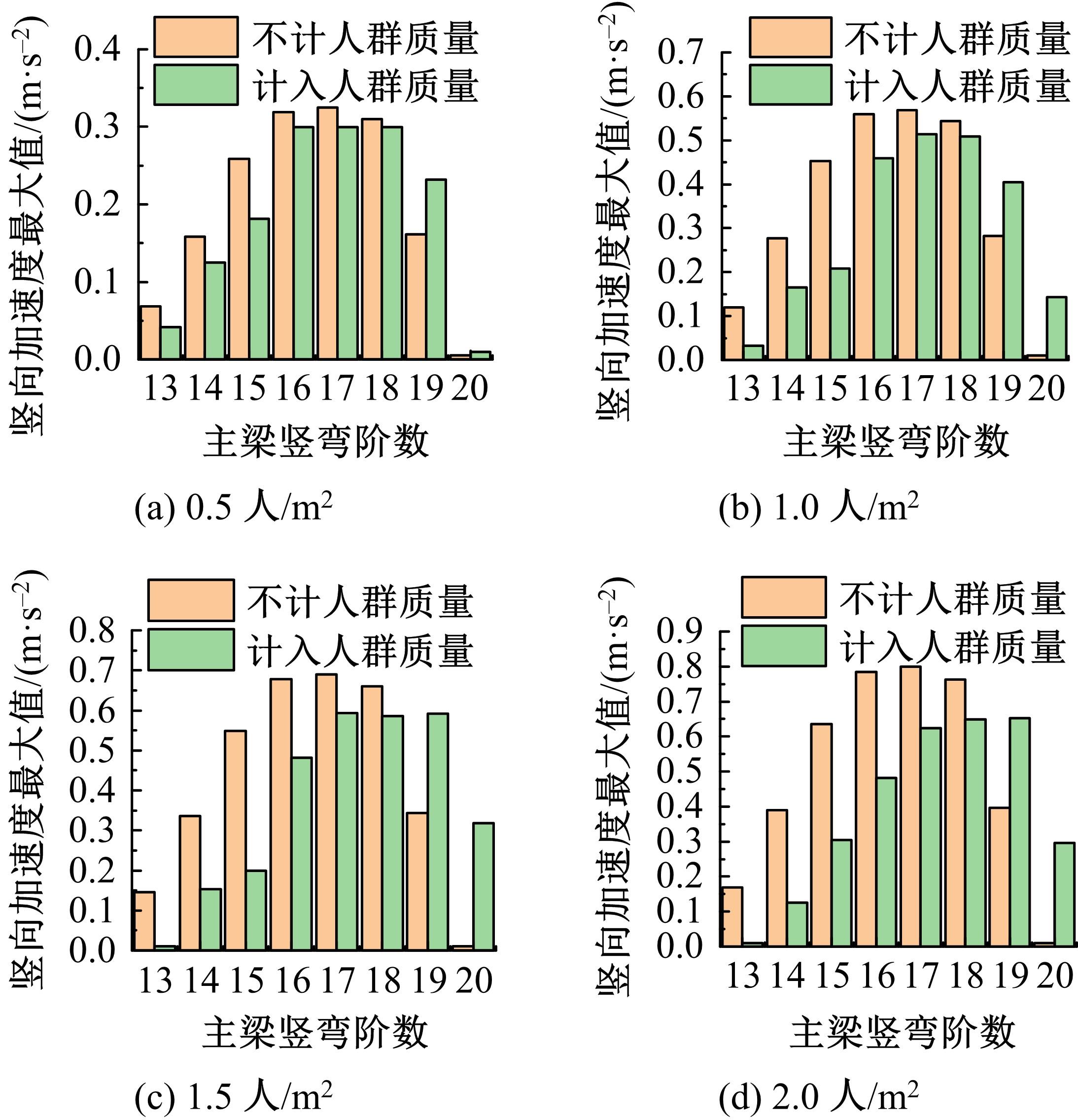
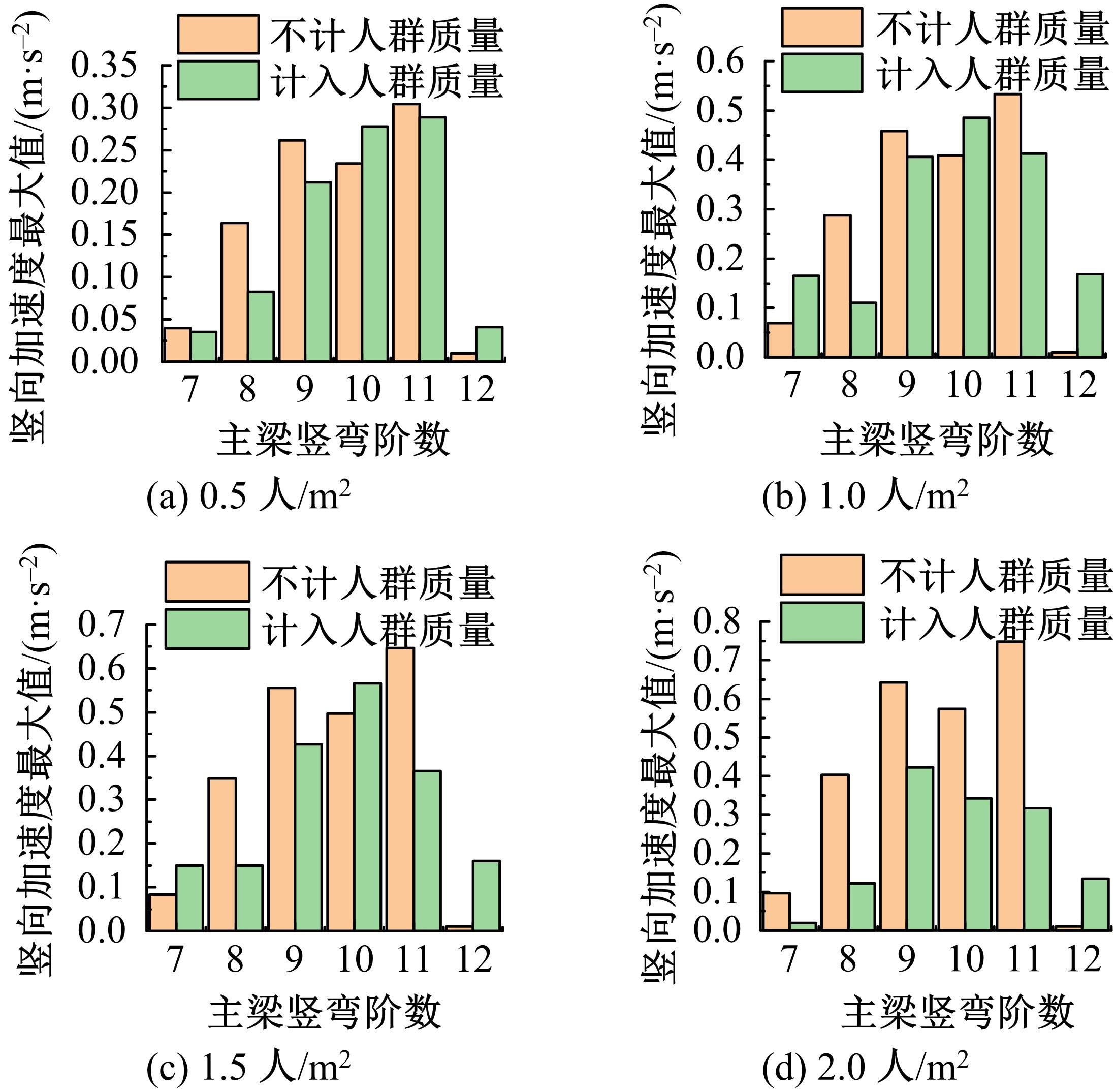
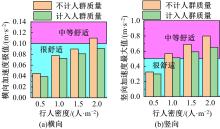
为研究结构细节对人行悬索桥人致振动响应及行人舒适度的影响,以某人行玻璃悬索桥为工程实例,分别建立了竖直吊杆模型和倾斜吊杆模型,分析了不同吊杆对自振特性和人致振动响应的影响,并基于德国EN03规范对行人舒适度进行了评估.结果表明:竖直吊杆模型横向及竖向基频均小于倾斜吊杆模型,但两种吊杆模型下该桥的振动频率均较低,说明结构整体柔性较大;两种吊杆模型中,计入人群质量后,各阶自振频率和主梁最大加速度均随行人密度的增加而减小;同一人流量下,主梁在对应不同模态的行人步频下加速度最大值均不同,但同一工况下倾斜吊杆模型的横弯和竖弯加速度数值均较竖直吊杆模型有所下降;两种吊杆模型的横向舒适度综合评价相同,竖向舒适度综合评价倾斜吊杆模型更优,倾斜吊杆可以有效加强改人行悬索桥的横向和竖向刚度。
中图分类号:
- U448.25
| 1 | 陈舟, 颜全胜, 贾布裕, 等. 行走激励下人行桥振动响应简化计算[J]. 哈尔滨工程大学学报, 2018, 39(3): 483-489. |
| Chen Zhou, Yan Quan-sheng, Jia Bu-yu, et al. Simplified calculation on the vibration response of a footbridge under human walking loads[J]. Journal of Harbin Engineering University, 2018, 39(3): 483-489. | |
| 2 | 李泽民,吴冬雁,刘宣含,等. 真实步伐荷载作用下人行桥振动及共振加速分析[J]. 噪声与振动控制, 2019, 39(6): 164-168. |
| Li Ze-min, Wu Dong-yan, Liu Xuan-han, et al. Vibration and resonance response analysis of footbridges under actual walking load[J]. Noise and Vibration Control, 2019, 39(6): 164-168. | |
| 3 | 汪志昊,寇琛,刘召朋,等. 人体姿态对人-结构耦合系统竖向动力特性影响试验研究[J]. 振动与冲击,2019, 38(19): 58-63. |
| Wang Zhi-hao, Kou Chen, Liu Zhao-peng, et al. Tests for effects of human body posture on vertical dynamic characteristics of a human- structure interaction system[J]. Jounal of Vibation and Shock, 2019, 38(19): 58-63. | |
| 4 | 谢伟平,汤宗恒,何卫. 多人-桥竖向动力相互作用研究[J]. 振动与冲击, 2020, 39(11): 76-82. |
| Xie Wei-ping, Tang Zong-heng, He Wei. Study on vertical vibration of bridge-pedestrians dynamic interaction system[J]. Journal of Vibration and Shock, 2020, 39(11): 76-82. | |
| 5 | 张琼, 南娜娜, 朱前坤, 等. 基于社会力模型的人群-桥梁竖向动力耦合效应研究[J]. 振动与冲击,2020, 39(9): 71-79. |
| Zhang Qiong, Na-na Nan, Zhu Qian-kun, et al. Analysis on the vertical coupled dynamic effect of a crowd-bridge system based on the social force model [J]. Journal of Vibration and Shock, 2020, 39(9):71-79. | |
| 6 | 操礼林,吕亚兵,曹栋,等. 行人动力学参数对大跨简支人行桥人致振动的影响分析[J]. 东南大学学报: 自然科学版, 2020, 50(2): 260-266. |
| Cao Li-lin, Ya-bing Lyu, Cao Dong, et al. Influence analysis of pedestrian dynamic parameters on human- induced vibration of long span simply supported footbridge[J]. Journal of Southeast University(Natural Science Edition), 2020, 50(2): 260-266. | |
| 7 | 王晋平,熊杰程,陈隽.人群步行荷载的互谱模型及应用[J]. 土木工程学报, 2020, 53(7): 12-20. |
| Wang Jin-ping, Xiong Jie-cheng, Chen Jun. Cross-spectral model for crowd walking load and its application[J]. China Civil Engineering Journal, 2020, 53(7): 12-20. | |
| 8 | 贾布裕,颜全胜,余晓琳,等. 考虑行人随机性的人行桥人致横向振动稳定性分析[J]. 工程力学, 2019, 36(1): 155-164. |
| Jia Bu-yu, Yan Quan-sheng, Yu Xiao-lin, et al. Stability analysis on pedestrian-induced lateral vibration of footbridges considering pedestrian stochastic excitation[J]. Engineering Mechanics, 2019, 36(1): 155-164. | |
| 9 | Han H, Zhou D, Ji T, et al. Modelling of lateral forces generated by pedestrians walking across footbridges[J]. Applied Mathematical Modelling, 2021, 89: 1775-1791. |
| 10 | Lai E, Gentile C, Mulas M G. Experimental and numerical serviceability assessment of a steel suspension footbridge[J]. Journal of Constructional Steel Research, 2017, 132: 16-28. |
| 11 | Bedon C. Diagnostic analysis and dynamic identification of a glass suspension footbridge via on-site vibration experiments and FE numerical modeling[J]. Composite Structures, 2019, 216: 366-378. |
| 12 | Bedon C. Experimental investigation on vibration sensitivity of an indoor glass footbridge to walking conditions[J]. Journal of Building Engineering, 2020, 29: 1-17. |
| 13 | 邹卓,宋旭明,李璋,等. 基于TMD的自锚式人行悬索桥人致振动控制研究[J]. 铁道科学与工程学报, 2018, 15(10): 2574-2582. |
| Zou Zhuo, Song Xu-ming, Li Zhang, et al. Study of pedestrian-induced vibration of self-anchored suspension footbridge based on TMD[J]. Journal of Railway Science and Engineering, 2018, 15(10): 2574-2582. | |
| 14 | Dong C Z, Bas S, Catbas N. Investigation of vibration serviceability of a footbridge using computer vision-based methods[J]. Engineering Structures, 2020, 224: 1-13. |
| 15 | Pampa D, Sriram N, Scott W. Reliability-based assessment and calibration of standards for the lateral vibration of pedestrian bridges[J]. Engineering Structures, 2021, 239: 1-13. |
| 16 | Research Fund for Coal and Steel, HiVoSS: Design of Footbridges [S]. |
| 17 | 王保群,张强勇,张凯,等. 自锚式斜拉-悬吊协作体系桥梁动力性能[J]. 吉林大学学报: 工学版, 2009, 39(3): 686-690. |
| Wang Bao-qun, Zhang Qiang-yong, Zhang Kai, et al. Dynamic characteristics for self-anchored cable-stayed suspension bridges[J]. Journal of Jilin University(Engineering and Technology Edition), 2009, 39(3): 686-690. | |
| 18 | 钟昌均,王忠彬,柳晨阳.悬索桥主索鞍承载力影响因素及结构优化[J]. 吉林大学学报: 工学版, 2021, 51(6): 2068-2078. |
| Zhong Chang-jun, Wang Zhong-bin, Liu Chen-yang. Influencing factors and structural optimization of main cable saddle bearing capacity of suspension bridge[J]. Journal of Jilin University(Engineering and Technology Edition), 2021, 51(6): 2068-2078. |
| [1] | 叶华文,段智超,刘吉林,周渝,韩冰. 正交异性钢⁃混组合桥面的轮载扩散效应[J]. 吉林大学学报(工学版), 2022, 52(8): 1808-1816. |
| [2] | 王立峰,肖子旺,于赛赛. 基于Bayesian网络的多塔斜拉桥挂篮系统风险分析的新方法[J]. 吉林大学学报(工学版), 2022, 52(4): 865-873. |
| [3] | 钟昌均,王忠彬,柳晨阳. 悬索桥主索鞍承载力影响因素及结构优化[J]. 吉林大学学报(工学版), 2021, 51(6): 2068-2078. |
| [4] | 陈巍,万田保,王忠彬,厉萱,沈锐利. 悬索桥主缆除湿的内部送气管道设计与性能[J]. 吉林大学学报(工学版), 2021, 51(5): 1749-1755. |
| [5] | 郭殊伦,钟铁毅,闫志刚. 大跨度斜拉桥拉索的抖振响应计算方法[J]. 吉林大学学报(工学版), 2021, 51(5): 1756-1762. |
| [6] | 高凯,刘纲. 全局临界强度分枝-约界法的有效强度改进[J]. 吉林大学学报(工学版), 2021, 51(2): 597-603. |
| [7] | 宫亚峰,宋加祥,谭国金,毕海鹏,刘洋,单承新. 多车桥梁动态称重算法[J]. 吉林大学学报(工学版), 2021, 51(2): 583-596. |
| [8] | 孔庆雯,谭国金,王龙林,王勇,魏志刚,刘寒冰. 基于有限元方法的裂缝箱梁桥自振特性分析[J]. 吉林大学学报(工学版), 2021, 51(1): 225-232. |
| [9] | 陈华,陈耀嘉,谢斌,王鹏凯,邓朗妮. CFRP筋粘结式锚固体系界面失效演化机制及粘结强度计算[J]. 吉林大学学报(工学版), 2020, 50(5): 1698-1708. |
| [10] | 宫亚峰,宋加祥,毕海鹏,谭国金,胡国海,林思远. 装配式箱涵结构缩尺模型静载试验及有限元分析[J]. 吉林大学学报(工学版), 2020, 50(5): 1728-1738. |
| [11] | 高昊,王君杰,刘慧杰,王剑明. 连续梁桥地震行为可控设计准则及实用装置[J]. 吉林大学学报(工学版), 2020, 50(5): 1718-1727. |
| [12] | 蒲黔辉,刘静文,赵刚云,严猛,李晓斌. 高性能树脂混凝土加固混凝土偏压柱承载力理论分析[J]. 吉林大学学报(工学版), 2020, 50(2): 606-612. |
| [13] | 张云龙,郭阳阳,王静,梁东. 钢-混凝土组合梁的固有频率及其振型[J]. 吉林大学学报(工学版), 2020, 50(2): 581-588. |
| [14] | 王伯昕,杨海涛,王清,高欣,陈小旭. 基于补充改进集合经验模态分析法⁃多尺度排列熵分析桥梁振动信号优化滤波方法[J]. 吉林大学学报(工学版), 2020, 50(1): 216-226. |
| [15] | 张淼,钱永久,张方,朱守芹. 基于增大截面法的混凝土加固石拱桥空间受力性能试验分析[J]. 吉林大学学报(工学版), 2020, 50(1): 210-215. |
|
||