车辆转向非线性平衡状态求解及其稳定性确定

doi:10.13229/j.cnki.jdxbgxb.20220061

摘要/Abstract

摘要：

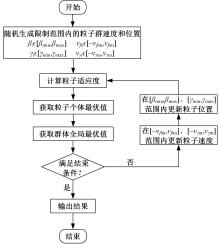
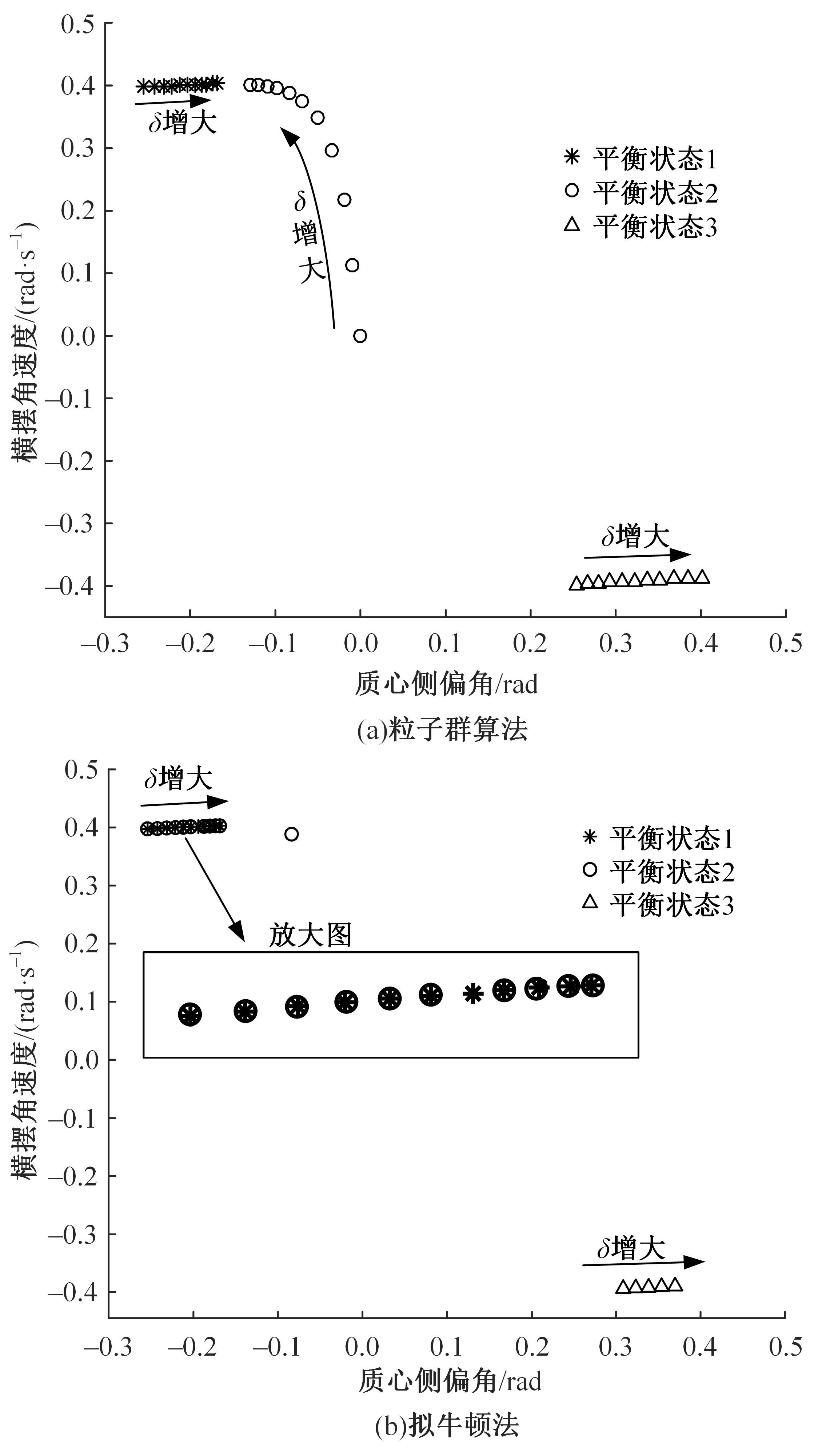
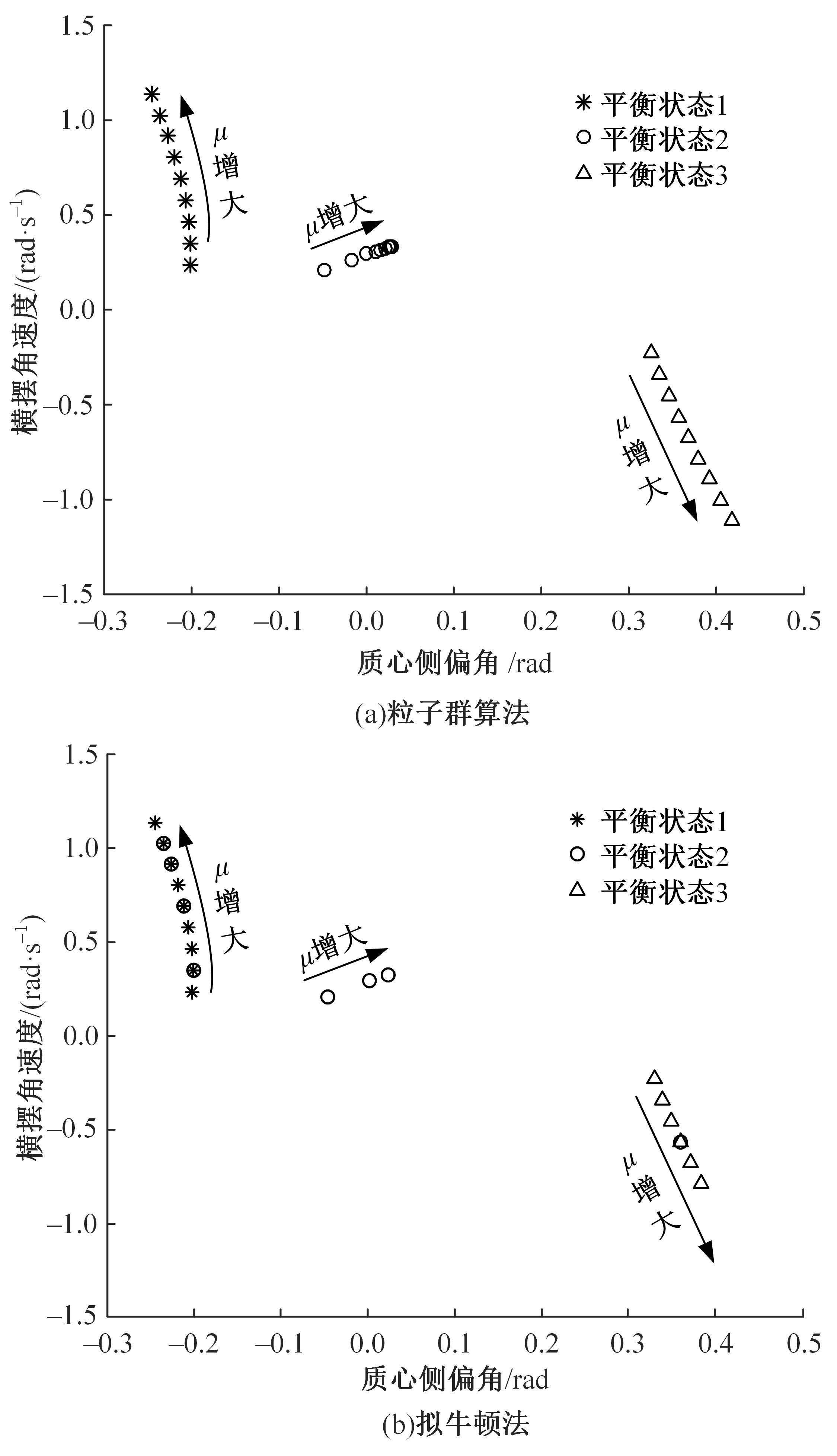
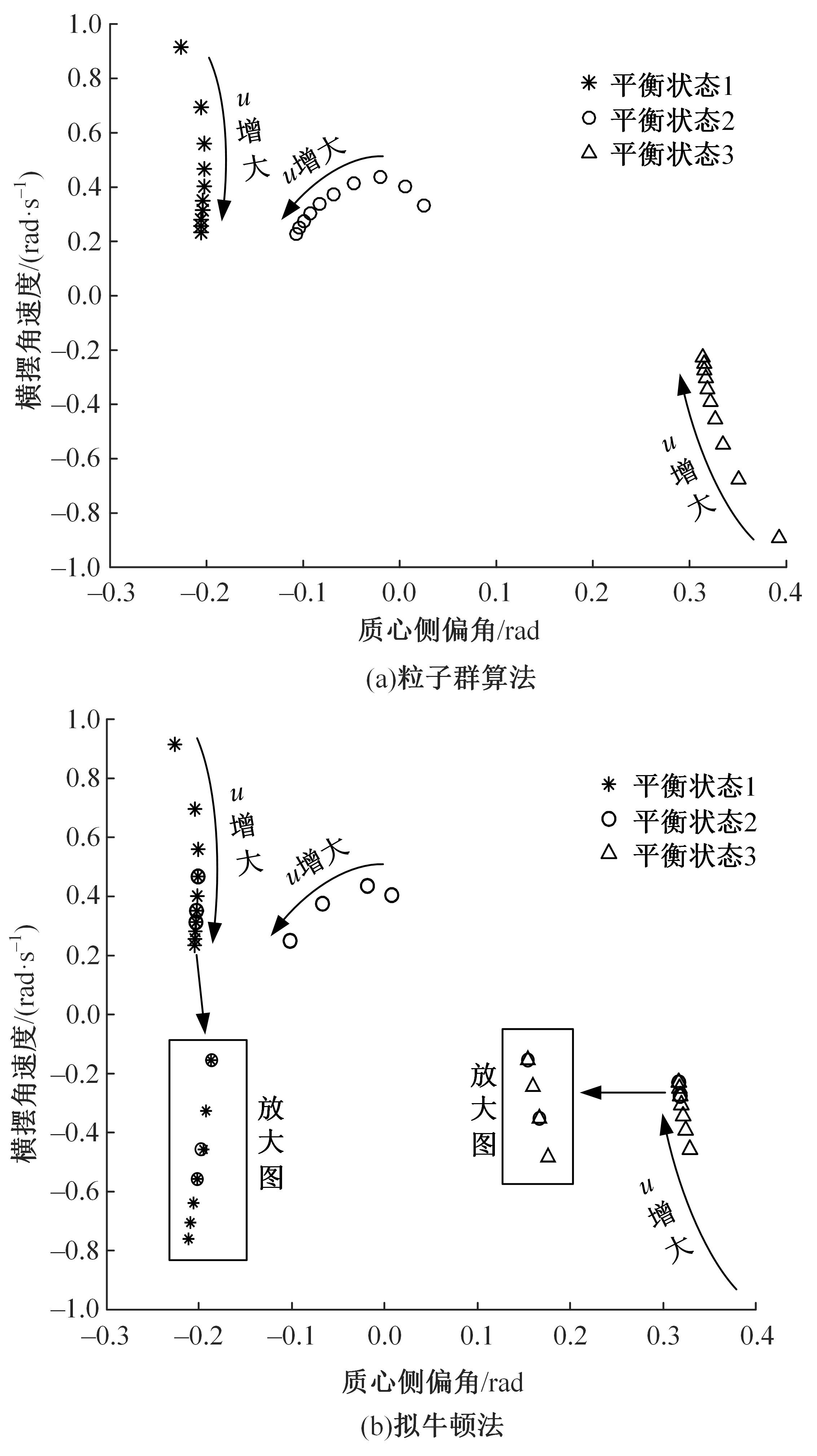
针对车辆转向非线性平衡状态及其稳定性确定问题，提出了求解车辆转向非线性二自由度模型平衡状态的一种新方法及其稳定性判据。首先，建立了车辆转向非线性二自由度模型，采用简化魔术公式轮胎模型描述了轮胎非线性侧向力。然后，提出了求解相应模型转向非线性平衡状态的粒子群算法，通过理论分析得到平衡状态稳定性判据。最后，设计了前轮转角、路面附着系数和车速分别变化的3种行驶条件，应用粒子群算法和拟牛顿法对3种行驶条件下的转向非线性平衡状态进行了求解和稳定性判断。结果表明，本文方法可以准确求解车辆转向非线性二自由度模型平衡状态，求解效果优于拟牛顿法，稳定性判据适用于确定平衡状态的稳定性。

关键词: 车辆工程, 非线性, 转向稳定性, 平衡状态, 车辆转向二自由度模型, 粒子群算法

Abstract:

Aiming at the problem of vehicle steering nonlinear equilibrium state and its stability determination， a new method for solving the equilibrium state of vehicle steering nonlinear two degree of freedom model and its stability criterion was proposed. Firstly， the nonlinear two degree of freedom model of vehicle steering was established， and the simplified magic formula tire model was used to describe the nonlinear tire lateral force. Then， the particle swarm optimization algorithm for solving the nonlinear equilibrium state of the corresponding model was established， and the stability criterion of the equilibrium state was deduced through theoretical analysis. Finally， three driving conditions with different front wheel steer angle， road adhesion coefficient and vehicle speed were designed， and the particle swarm optimization algorithm and the quasi Newton method were used to solve the steering nonlinear equilibrium state under the three driving conditions and to judge the stability of three kinds of driving conditions respectively. The results show that the proposed method can accurately solve the equilibrium state of the vehicle steering nonlinear two degree of freedom model， the solution effect is better than the quasi Newton method， and the stability criterion is suitable for determining the stability of the equilibrium state.

Key words: vehicle engineering, nonlinearity, steering stability, equilibrium state, two degree of freedom vehicle steering model, particle swarm optimization （PSO）

中图分类号:

U461.6

李杰,贾长旺,赵旗. 车辆转向非线性平衡状态求解及其稳定性确定[J]. 吉林大学学报(工学版), 2023, 53(12): 3326-3334.

Jie LI,Chang-wang JIA,Qi ZHAO. Solution of nonlinear equilibrium state of vehicle steering and its stability determination[J]. Journal of Jilin University(Engineering and Technology Edition), 2023, 53(12): 3326-3334.

图/表 7

图1

表1

车辆参数"

参数	数值
车辆总质量 $m$ /kg	1022
横摆转动惯量 $I z$ /（kg·m²）	1471.7
质心到前轴距离 $a$ /m	1.197
质心到后轴距离 $b$ /m	1.123
前轴轮胎参数 $C f$	1.162
前轴轮胎参数 $B f$	0.2
后轴轮胎参数 $C r$	1.313
后轴轮胎参数 $B r$	0.25

表1

表2

粒子群算法参数"

参数	数值
维数 $n$	2
粒子数目 $N$	50
最大迭代数 $M$	200
精度 $ε$	$10 - 4$
学习因子 $c 1$	1.5
学习因子 $c 2$	2.5
惯性权重 $w$	0.5
侧偏角位置范围 $[β m i n, β m a x]$	［-1，1］
横摆角速度位置范围 $[γ m i n, γ m a x]$	［-2，2］
侧偏角速度范围 $[- v β m, v β m]$	［-0.2，0.2］
横摆角速度范围 $[- v γ m, v γ m]$	［-0.5，0.5］

表2

表3

u=70 km/h和μ=0.8时粒子群算法求解转向平衡状态"

平衡状态	前轮转角 $δ$ /rad	质心侧偏角 $β$ /rad	横摆角速度 $γ$ /（rad·s^-1）	适应值/10^-4
1	0	-0.2541	0.3975	0.5443
	0.02	-0.2425	0.3984	0.6840
	0.04	-0.2315	0.3993	0.9469
	0.06	-0.2213	0.3999	0.9681
	0.08	-0.2118	0.4006	0.8373
	0.10	-0.2030	0.4012	0.4632
	0.12	-0.1949	0.4017	0.0342
	0.14	-0.1875	0.4022	0.2721
	0.16	-0.1807	0.4025	0.6581
	0.18	-0.1745	0.4028	0.3866
	0.20	-0.1690	0.4030	0.9367
2	0	0	0	0.4808
	0.02	-0.0089	0.1135	0.6065
	0.04	-0.0197	0.2167	0.6575
	0.06	-0.0339	0.2974	0.4478
	0.08	-0.0510	0.3485	0.6475
	0.1	-0.0684	0.3753	0.2146
	0.12	-0.0842	0.3887	0.2247
	0.14	-0.0981	0.3955	0.0242
	0.16	-0.1101	0.3991	0.8736
	0.18	-0.1208	0.4010	0.9344
	0.20	-0.1304	0.4023	0.6673
3	0	0.2540	-0.3976	0.5801
	0.02	0.2664	-0.3966	0.5494
	0.04	0.2793	-0.3956	0.4685
	0.06	0.2929	-0.3948	0.8474
	0.08	0.3070	-0.3938	0.8171
	0.1	0.3217	-0.3927	0.9006
	0.12	0.3368	-0.3917	0.7133
	0.14	0.3523	-0.3906	0.4010
	0.16	0.3682	-0.3897	0.3474
	0.18	0.3845	-0.3888	0.3639
	0.20	0.4011	-0.3878	0.7732

表3

图2

图3

图4

参考文献 25

1	One E, Hosoe S, Tuan H D, et al. Bifurcation in vehicle dynamics and robust front wheel steering control[J]. IEEE Trans Control Systems Technology, 1998, 6(3): 412-420.
2	Azadi S, Naghibian M, Kazemi R. Adaptive integrated control design for vehicle dynamics using phase-plane analysis[J]. Journal of Mechanical Science and Technology, 2015, 29(6): 2477-2485.
3	刘飞, 熊璐, 邓律华, 等. 基于相平面法的车辆行驶稳定性判定方法[J]. 华南理工大学学报: 自然科学版, 2014, 42(11): 63-70.
	Liu Fei, Xiong Lu, Deng Lv-hua, et al. Vehicle stability criterion based on phase plane method[J]. Journal of South China University of Technology(Natural Science Edition), 2014, 42(11): 63-70.
4	熊璐, 曲彤, 冯源, 等. 极限工况下车辆行驶的稳定性判据[J]. 机械工程学报, 2015, 51(10): 103-111.
	Xiong Lu, Qu Tong, Feng Yuan, et al. Stability criterion for the vehicle under critical driving situation[J]. Journal of Mechanical Engineering, 2015, 51(10): 103-111.
5	Wei L, Lu X, Bo L, et al. Vehicle stability criterion research based on phase plane method[C]∥SAE Paper, 2017-01-1560.
6	张玮, 张树培, 罗崇恩, 等. 智能汽车紧急工况避撞轨迹规划[J]. 吉林大学学报:工学版, 2022, 52(7): 1515-1523.
	Zhang Wei, Zhang Shu-pei, Luo Chong-en, et al. Collision avoidance trajectory planning for intelligent vehicles in emergency conditions[J]. Journal of Jilin University (Engineering and Technology Edition), 2022, 52(7): 1515-1523.
7	Chung T, Yi K. Design and evaluation of side slip angle-based vehicle stability control scheme on a virtual test track[J]. IEEE Transactions on Control Systems Technology, 2006, 14(2): 224-234.
8	Bobiertiu C G, Beal C E, Keglman J C, et al. Vehicle control synthesis using phase portraits of planar dynamics[J]. Vehicle System Dynamics, 2019, 57(9): 1318-1337.
9	金立生, 谢宪毅, 高琳琳, 等. 基于二次规划的分布式电动汽车稳定性控制[J]. 吉林大学学报: 工学版, 2018, 48(5): 1349-1359.
	Jin Li-sheng, Xie Xian-yi, Gao Lin-lin, et al. Distributed electric vehicle stability control based on quadratic programming[J]. Journal of Jilin University (Engineering and Technology Edition), 2018, 48(5): 1349-1359.
10	Shen S W, Wang J, Shi P, et al. Nonlinear dynamics and stability analysis of vehicle plane motions[J]. Vehicle System Dynamics, 2007, 45(1): 15-35.
11	杨秀建, 王增才. 高维汽车侧向动力学系统的分岔与失稳分析[J]. 农业机械学报, 2008, 39(12): 45-50, 77.
	Yang Xiu-jian, Wang Zeng-cai. Analysis on bifurcation and destabilization of high-dimensional vehicle lateral dynamics[J]. Transactions of the Chinese Society for Agricultural Machinery, 2008, 39(12): 45-50, 77.
12	杨秀建, 王增才, 朱淑亮, 等. 汽车稳态转向失稳的最近分岔点实时追踪[J]. 农业机械学报, 2009, 40(1): 20-25.
	Yang Xiu-jian, Wang Zeng-cai, Zhu Shu-liang, et al. Real-time tracking of the closest bifurcation for vehicle steady-state cornering stability[J]. Transactions of the Chinese Society for Agricultural Machinery, 2009, 40(1): 20-25.
13	Horiuchi S, Okada K, Nohtomi S. Analysis of accelerating and braking stability using constrained bifurcation and continuation methods[J]. Vehicle System Dynamics, 2008, 46(Sup.1): 585-597.
14	Della R F, Gobbi M, Mastinu G, et al. Bifurcation analysis of a car and driver model[J]. Vehicle System Dynamics, 2014, 52(1): 142-156.
15	Della R F, Mastinu G. Analysis of the lateral dynamics of a vehicle and driver model running straight ahead[J]. Nonlinear Dynamics, 2018, 92(1): 97-106.
16	刘丽. 车辆三自由度平面运动稳定性的非线性分析及控制策略评价[D]. 长春:吉林大学交通学院, 2010.
	Liu Li. Nonlinear analysis and control strategy evaluation on the stability of vehicle 3-DOF planar motion[D]. Changchun: College of Transportation, Jilin University, 2010.
17	王宪彬, 施树明, 刘丽, 等. 基于遗传算法和拟牛顿法的车辆动力学平衡点混合求解方法[J]. 机械工程学报, 2014, 50(4): 120-127.
	Wang Xian-bin, Shi Shu-ming, Liu Li, et al. Vehicle dynamics equilibriums solution search based on hybridization of genetic algorithm and quasi-newton method[J]. Journal of Mechanical Engineering, 2014, 50(4): 120-127.
18	王积伟,陆一心,吴振顺,等. 现代控制理论与工程[M]. 北京: 高等教育出版社, 2010.
19	余志生. 汽车理论[M]. 北京: 机械工业出版社, 2009.
20	Bakker E, Nyborg L, Pacejka H B. Tyre modeling for use in vehicle dynamics studies[C]∥SAE Paper, 870421.
21	Pacejka H B. Tyre and Vehicle Dynamic[M]. Oxford: Butterworth-Heinemann, 2002.
22	李杰, 高雄, 王维, 等. 基于UniTire模型的平顺性和操纵稳定性协同研究[J]. 汽车工程, 2018, 40(2): 127-132.
	Li Jie, Gao Xiong, Wang Wei, et al. A collaborative study on ride comfort and handling stability based on UniTire model [J]. Automotive Engineering, 2018, 40(2): 127-132.
23	潘峰, 李位星, 高琪. 粒子群优化算法与多目标优化[M]. 北京: 北京理工大学出版社, 2013.
24	徐开, 陈志刚, 赵靖华, 等. 基于粒子群算法的星敏感器布局设计[J]. 吉林大学学报: 工学版, 2019, 49(3): 972-978.
	Xu Kai, Chen Zhi-gang, Zhao Jing-hua, et al. Layout design method of star sensor based on particle swarm optimization algorithm[J]. Journal of Jilin University (Engineering and Technology Edition), 2019, 49(3): 972-978.
25	马昌凤. 最优化方法及其Matlab程序设计[M]. 北京: 科学出版社, 2010.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

[1]	陈兆玮,蒲前华. 弹性车轮对大跨斜拉桥车桥耦合振动的抑制特性[J]. 吉林大学学报(工学版), 2023, 53(9): 2519-2532.
[2]	刘平义,李晓婷,高偌霖,李海涛,魏文军,王亚. 车辆侧倾驱动机构设计与试验[J]. 吉林大学学报(工学版), 2023, 53(8): 2185-2192.
[3]	黄学劲,钟锦星,路京雨,赵霁,肖伟,袁新枚. 基于用户画像的电动汽车充电负荷预测方法[J]. 吉林大学学报(工学版), 2023, 53(8): 2193-2200.
[4]	张树培,夏明悦,张玮,陈钊,陈义祥. 考虑非线性刚度的间隙球铰碰撞动力学建模与仿真[J]. 吉林大学学报(工学版), 2023, 53(8): 2227-2235.
[5]	陈辉,邵亚军. 基于惯性基准多传感器耦合的路面谱测量方法[J]. 吉林大学学报(工学版), 2023, 53(8): 2254-2262.
[6]	翁渊瀚,李南. 基于时间序列模型的文本数据压缩存储算法[J]. 吉林大学学报(工学版), 2023, 53(7): 2109-2114.
[7]	李岩,张久鹏,陈子璇,黄果敬,王培. 基于PCA-PSO-SVM的沥青路面使用性能评价[J]. 吉林大学学报(工学版), 2023, 53(6): 1729-1735.
[8]	汪少华,储堃,施德华,殷春芳,李春. 基于有限时间扩张状态观测的HEV鲁棒复合协调控制[J]. 吉林大学学报(工学版), 2023, 53(5): 1272-1281.
[9]	陈鑫,张冠宸,赵康明,王佳宁,杨立飞,司徒德蓉. 搭接焊缝对铝合金焊接结构轻量化设计的影响[J]. 吉林大学学报(工学版), 2023, 53(5): 1282-1288.
[10]	张勇,毛凤朝,刘水长,王青妤,潘神功,曾广胜. 基于Laplacian算法的汽车外流场畸变网格优化[J]. 吉林大学学报(工学版), 2023, 53(5): 1289-1296.
[11]	刘洋,刘吉成. 基于大数据与粒子群的清洁能源协同优化调度方法[J]. 吉林大学学报(工学版), 2023, 53(5): 1443-1448.
[12]	陈磊,王杨,董志圣,宋亚奇. 一种基于转向意图的车辆敏捷性控制策略[J]. 吉林大学学报(工学版), 2023, 53(5): 1257-1263.
[13]	于贵申,陈鑫,武子涛,陈轶雄,张冠宸. AA6061⁃T6铝薄板无针搅拌摩擦点焊接头结构及性能分析[J]. 吉林大学学报(工学版), 2023, 53(5): 1338-1344.
[14]	田彦涛,黄兴,卢辉遒,王凯歌,许富强. 基于注意力与深度交互的周车多模态行为轨迹预测[J]. 吉林大学学报(工学版), 2023, 53(5): 1474-1480.
[15]	尹燕莉,黄学江,潘小亮,王利团,詹森,张鑫新. 基于PID与Q⁃Learning的混合动力汽车队列分层控制[J]. 吉林大学学报(工学版), 2023, 53(5): 1481-1489.