螺栓预紧连接可靠性灵敏度分析

doi:10.13229/j.cnki.jdxbgxb.20211164

摘要/Abstract

摘要：

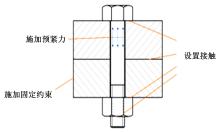
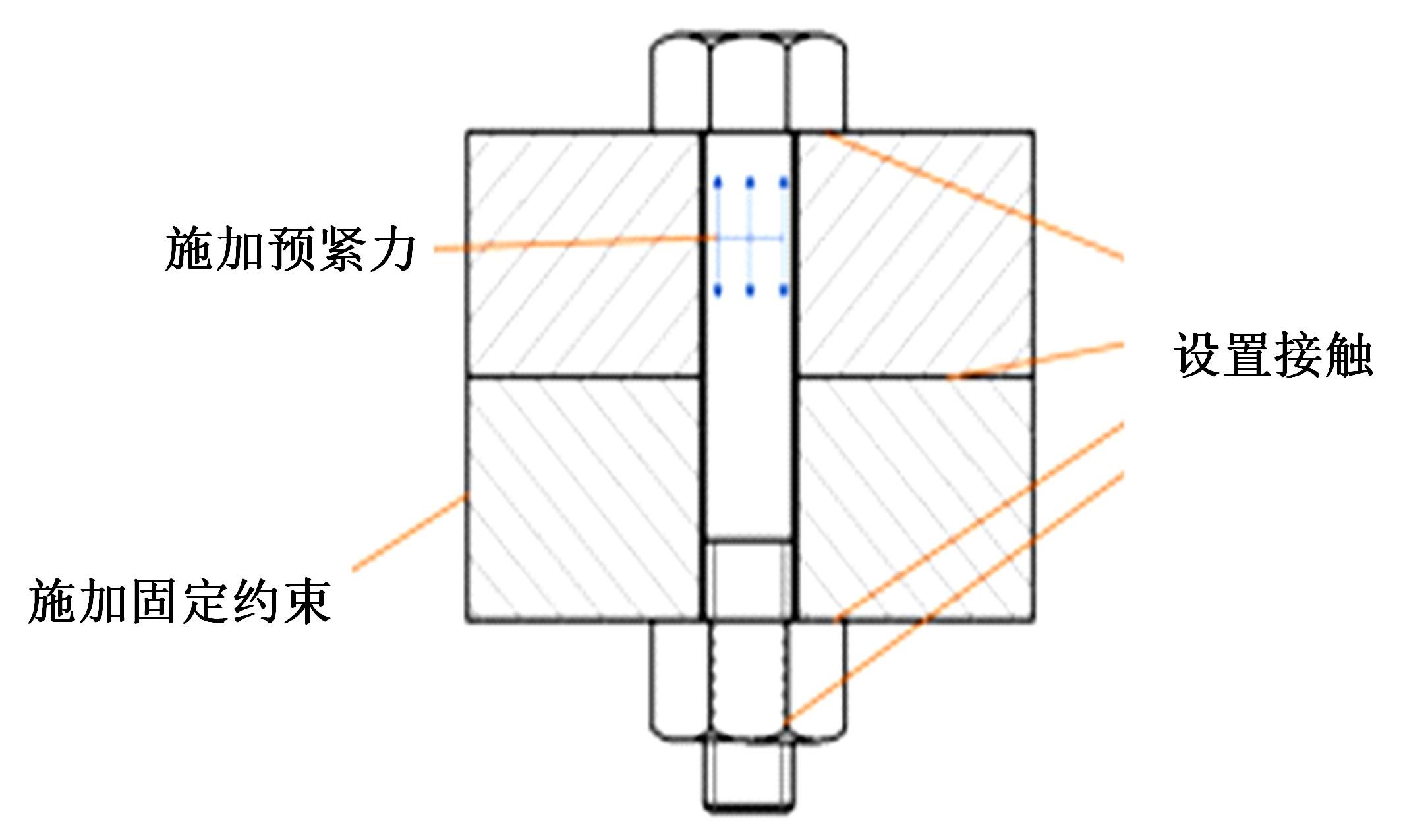
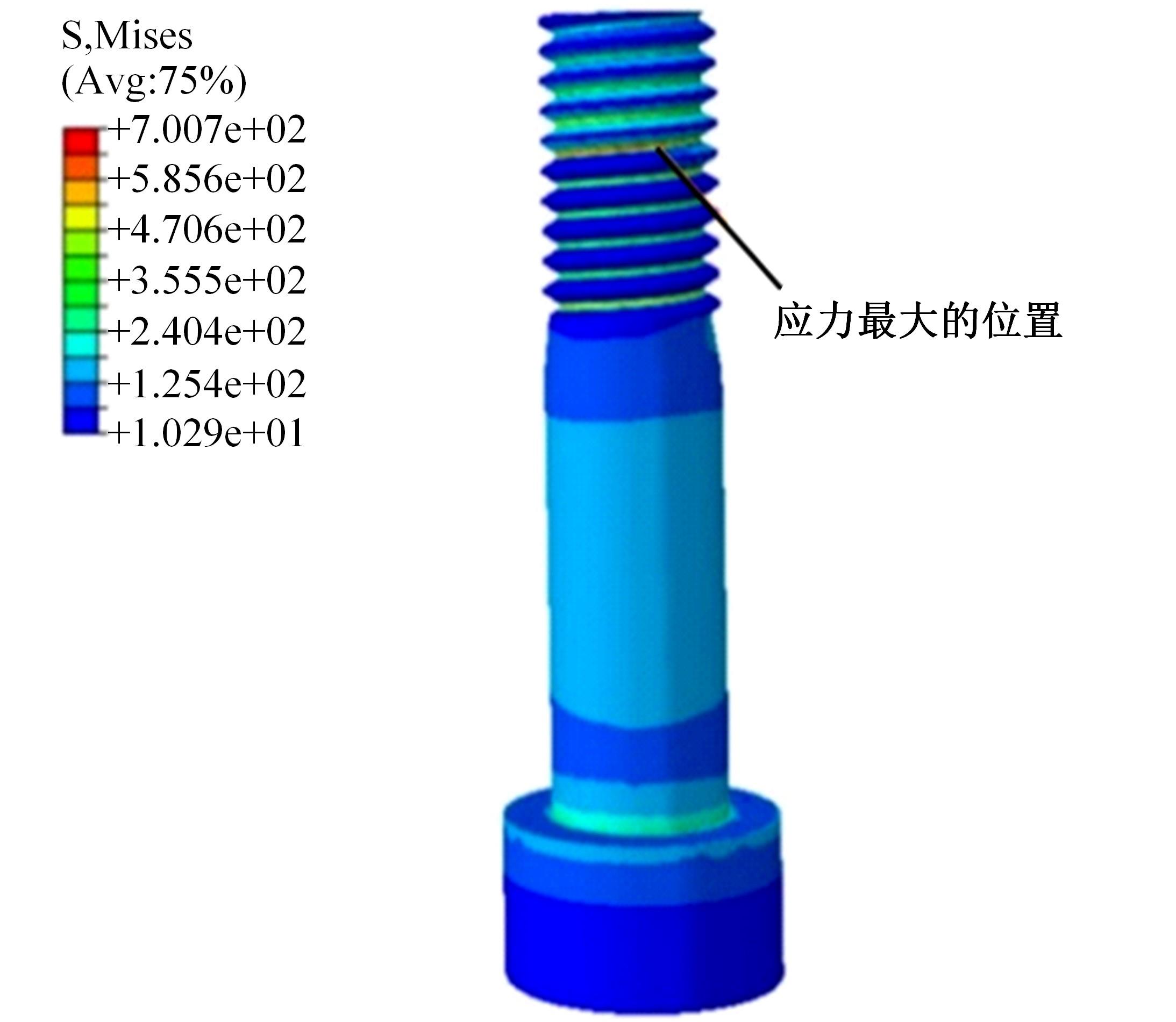
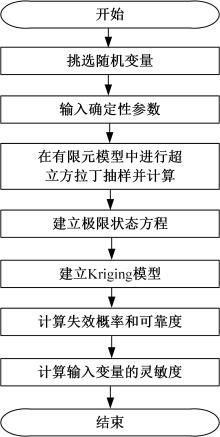
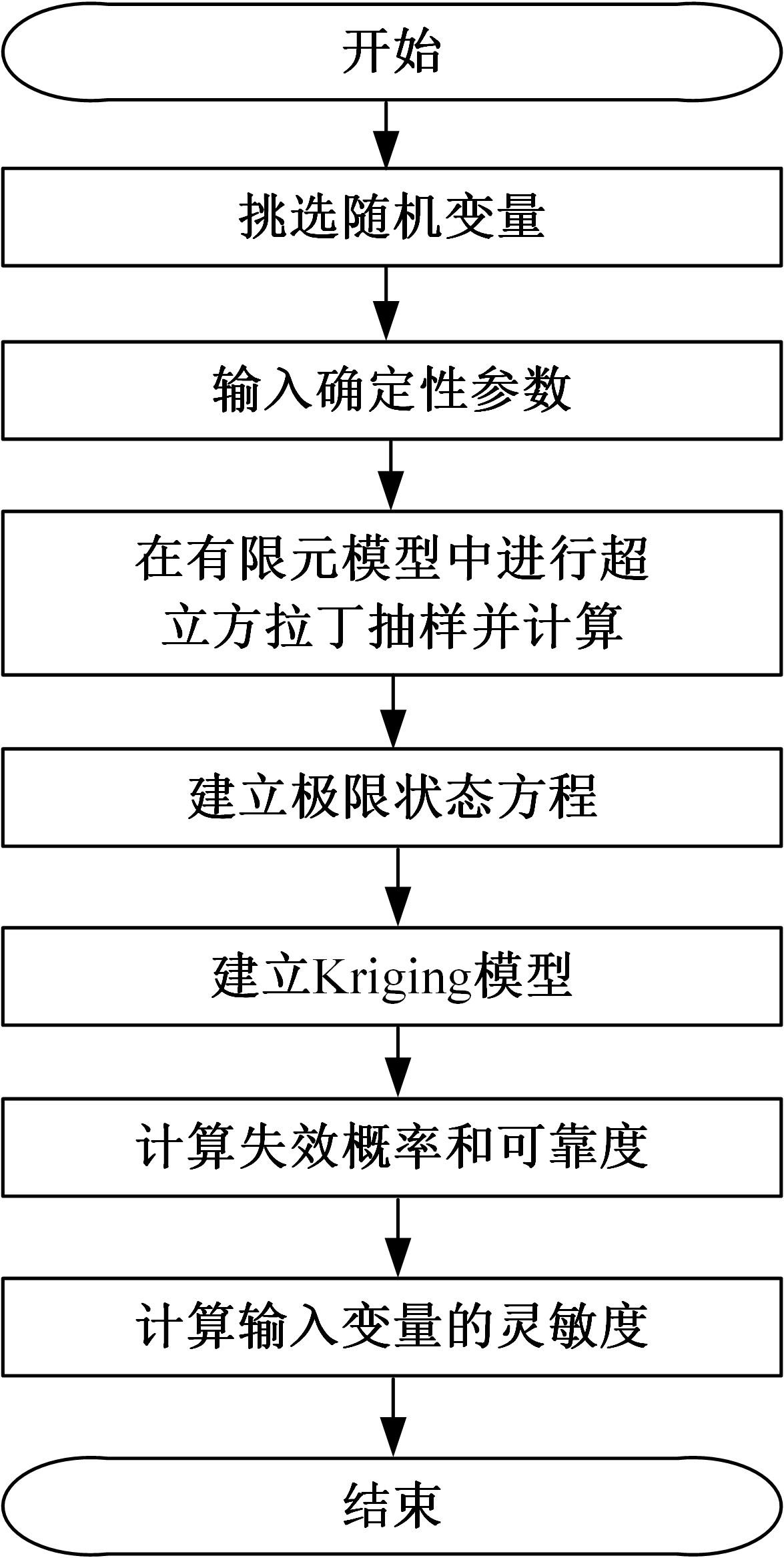
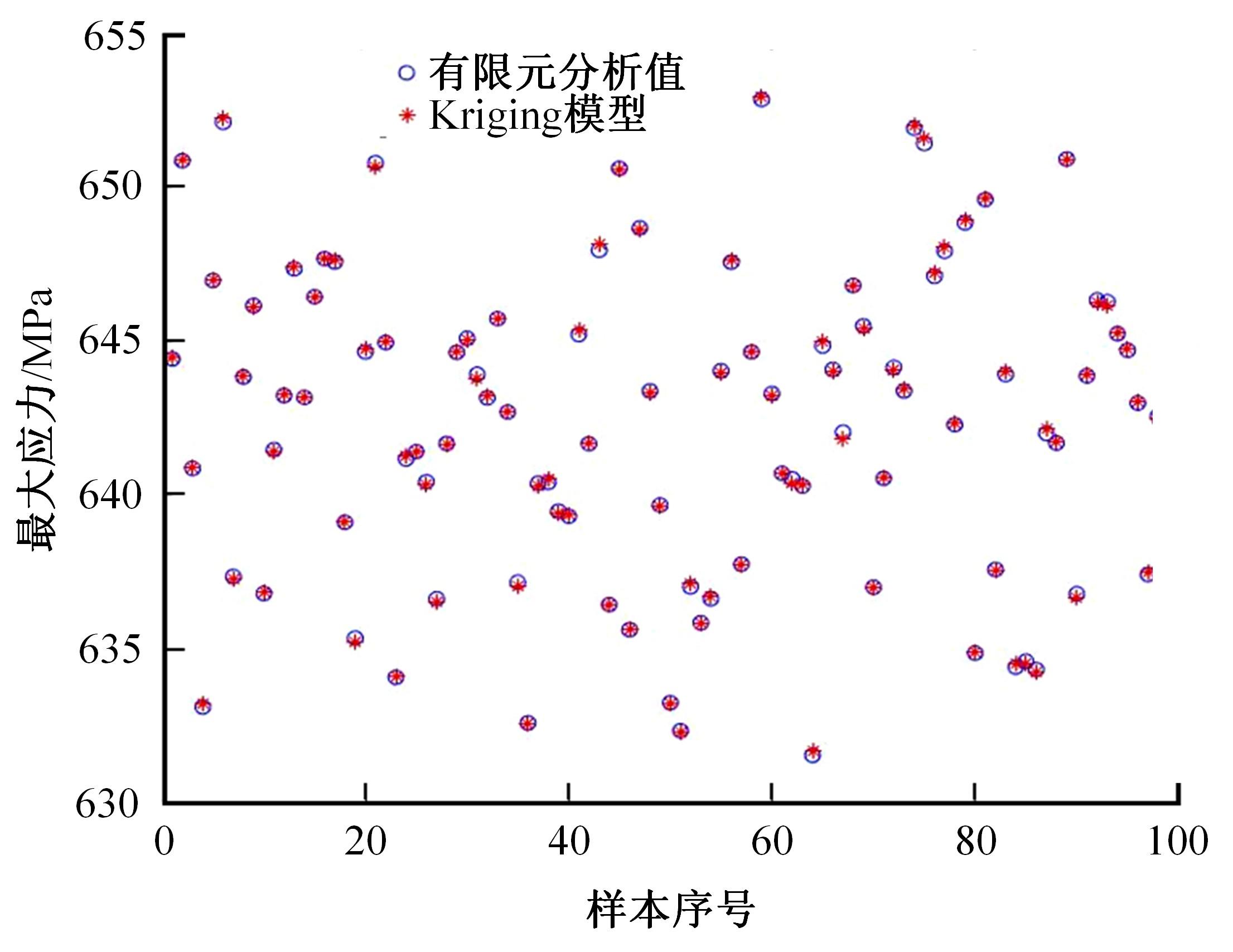
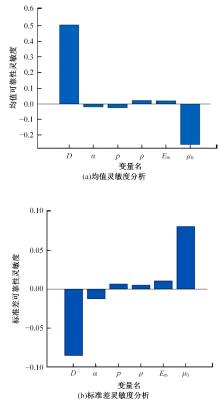
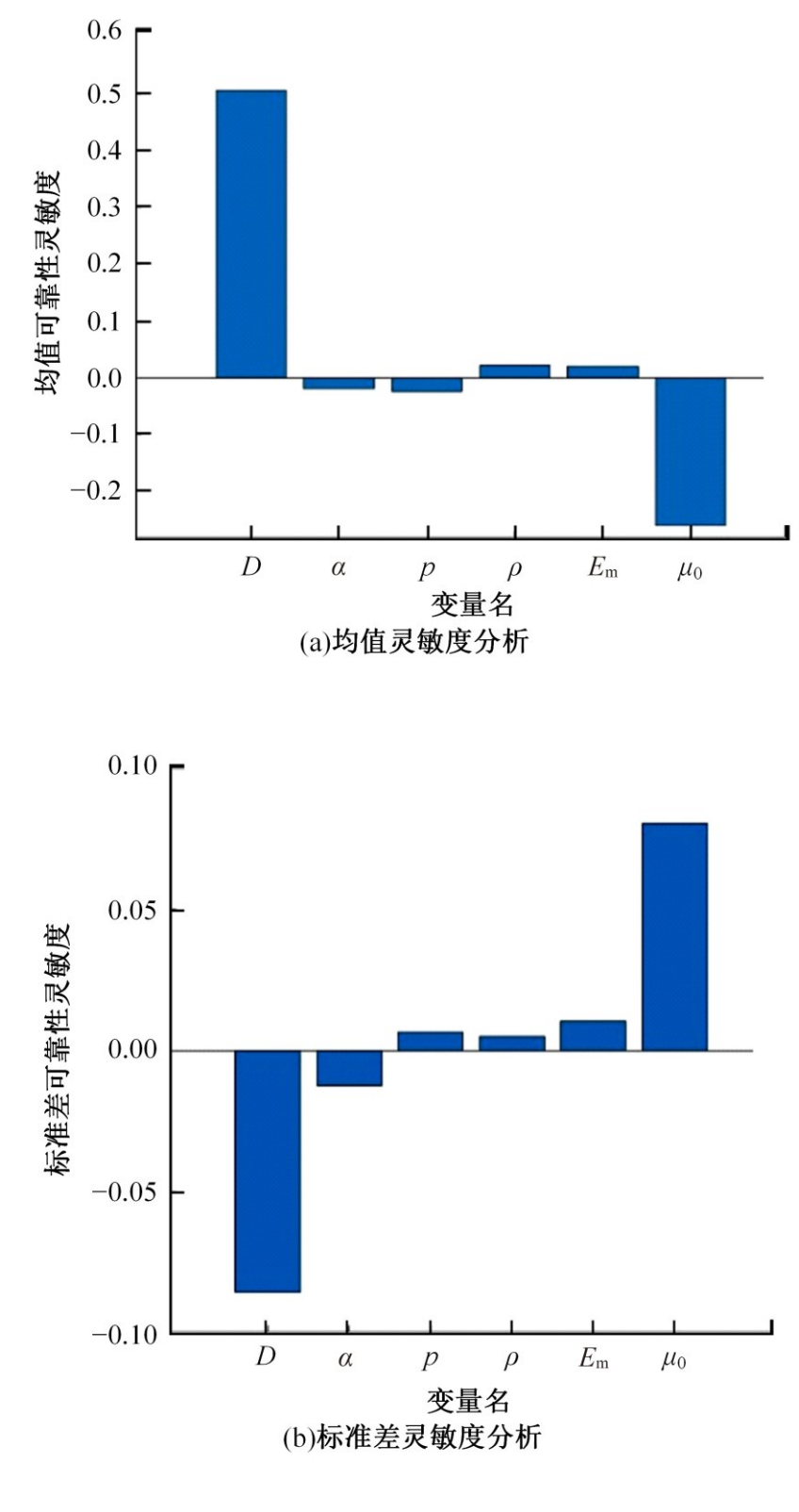
针对传统的螺栓预紧失效分析方法认为螺栓参数是确定的，而在实际螺栓连接中，各种结构参数的随机性将造成较大的分析误差的问题，考虑随机因素的影响，建立了一个螺栓预紧失效行为的有限元分析模型，以螺纹处的应力值是否超过屈服强度为判别条件进行可靠性分析，计算各参数对连接结构失效现象的灵敏度。研究结果表明：螺栓大径的变化对螺栓静强度失效的现象影响最大，材料的泊松比对其影响次之；螺栓连接的可靠度会随螺栓牙型角、螺距和材料泊松比的增大而增加，随螺栓大径以及材料的密度、弹性模量的增大而减小。

关键词: 机械设计, 螺栓连接, 静力学, 可靠性, 灵敏度

Abstract:

In bolt connection， excessive pre-tightening force will make bolts fail in case of accidental overload. Traditional method of bolt pre-tightening analysis considers that the parameters are determined， but the parameters are random in actual working conditions， which causes larger analysis errors. To solve this problem， considering the influence of random factors， a finite element analysis model of bolt pre-tightening failure behavior is proposed in this paper， the reliability analysis is carried out by judging whether the stress value at the thread of bolt exceeds the allowable stress value， and the reliability sensitivity analysis is calculated to evaluate the influence of various parameters on the failure phenomenon in bolt connection. The results show that the change of bolt diameter has the greatest influence on the phenomenon of bolt static strength failure， and the Poisson's ratio of material has the second influence on it. The reliability of bolt connection will increase with the increase of bolt tooth angle， screw pitch and Poisson's ratio of material， and decrease with the increase of bolt diameter， material density and elastic modulus.

Key words: machanical design, bolt connection, statics, reliability, sensitivity

中图分类号:

TH131.3

黄贤振,孙楷铂,栾晓刚,胡兵. 螺栓预紧连接可靠性灵敏度分析[J]. 吉林大学学报(工学版), 2023, 53(8): 2219-2226.

Xian-zhen HUANG,Kai-bo SUN,Xiao-gang LUAN,Bing HU. Reliability sensitivity analysis of bolt pre-tightening connection[J]. Journal of Jilin University(Engineering and Technology Edition), 2023, 53(8): 2219-2226.

图/表 11

图1

图2

表1

图3

图4

表2

表3

图5

表4

图6

图7

参考文献 23

1	Lin Q, Zhao Y, Sun Q, et al. Reliability evaluation method of anti-loosening performance of bolted joints[J]. Mechanical Systems and Signal Processing, 2022, 162(5): 108067.
2	Bozca M, Knt U. Reliability analysis of the mechanical properties of 30MnB4 high strength steel bolts under static loading conditions[J]. Ecological Restoration, 2020, 38(2): 495-512.
3	Öztekin E. Investigation of reliabilities of bolt distances for bolted structural steel connections by Monte Carlo simulation method[J]. Pamukkale University Journal of Engineering Sciences, 2015, 21(6): 213-223.
4	山本晃. 螺纹联接的理论与计算[M]. 1版. 上海: 上海科学技术文献出版社, 1984.
5	Sopwith D G. The distribution of load in screw threads[J]. Proceedings of the Institution of Mechanical Engineers, 2006, 159: 373-383.
6	Dragoni E. Effect of thread pitch and frictional coefficient on the stress concentration in metric nut-bolt connections[J]. Journal of Offshore Mechanics & Arctic Engineering, 1994, 116(1):21-27.
7	Zhao H. Stress concentration factors within bolt-nut connectors under elasto-plastic deformation[J]. International Journal of Fatigue, 1998, 20(9): 651-659.
8	Yokoyama T, Olsson M, Izumi S, et al. Investigation into the self-loosening behavior of bolted joint subjected to rotational loading[J]. Engineering Failure Analysis, 2012, 23(2): 35-43.
9	Dinger G, Friedrich C. Avoiding self-loosening failure of bolted joints with numerical assessment of local contact state[J]. Engineering Failure Analysis, 2011, 18(8): 2188-2200.
10	Fukuoka T, Nomura M. Proposition of helical thread modeling with accurate geometry and finite element analysis[J]. Journal of Pressure Vessel Technology, 2008, 130(1): 135-140.
11	胡大勇. 参数化三维螺纹实体建模技术及仿真研究[D]. 大连: 大连交通大学机械工程学院, 2005.
	Hu Da-yong. Parametric 3D thread solid modeling technology and simulation research[D]. Dalian: School of Mechanical Engineering, Dalian Jiaotong University, 2005.
12	侯世远. 螺纹联接松动机理研究[D]. 北京: 北京理工大学机械与车辆学院, 2015.
	Hou Shi-yuan. Research on the mechanism of thread connection looseness[D]. Beijing: School of Machinery and Vehicle, Beijing University of Technology, 2015.
13	陆秉权, 王海龙, 周小飞, 等. 应用有限元技术计算螺栓联接的方法研究[J]. 黑龙江电力, 2004, 26(2): 100-102.
	Lu Bing-quan, Wang Hai-long, Zhou Xiao-fei, et al. Research on the method of calculating bolted connections using finite element technology[J]. Heilongjiang Electric Power, 2004, 26 (2): 100-102.
14	李军, 杨洁明, 高俊云. 大型风力机组塔架螺栓连接应力分析[J]. 钢结构, 2011, 26(7): 22-25.
	Li Jun, Yang Jie-ming, Gao Jun-yun. Stress analysis of bolt connections in large wind turbine tower frames[J]. Steel Structures, 2011, 26(7): 22-25.
15	邱继伟, 罗海胜. 基于混合不确定性的螺旋锥齿轮结构可靠性分析[J]. 吉林大学学报: 工学版, 2022, 52(2): 466-473.
	Qiu Ji-wei, Luo Hai-sheng. Reliability analysis of spiral bevel gear structure based on mixed uncertainty [J]. Journal of Jilin University (Engineering and Techndogy Edition), 2022, 52(2): 466-473.
16	Jamia N, Jalali H, Taghipour J, et al. An equivalent model of a nonlinear bolted flange joint[J]. Mechanical Systems and Signal Processing, 2021, 153(25/26): 107507.
17	Izumi S, Yokoyama T, Kimura M, et al. Loosening-resistance evaluation of double-nut tightening method and spring washer by three-dimensional finite element analysis[J]. Engineering Failure Analysis, 2009, 16(5): 1510-1519.
18	Zou Q, Sun T S, Nassar S A, et al. Effect of lubrication on friction and torque-tension relationship in threaded fasteners[J]. Tribology Transactions, 2007, 50(1): 127-136.
19	李成, 朱红红, 铁瑛,等. 单搭胶/螺栓混合连接结构的应力分布与载荷分配[J]. 吉林大学学报: 工学版, 2013, 43(4): 933-938.
	Li Cheng, Zhu Hong-hong, Ying Tie, et al. Stress distribution and load distribution of single adhesive/bolt hybrid connection structure[J]. Journal of Jilin University(Engineering and Technology Edition), 2013, 43(4): 933-938.
20	Liu J H, Ouyang H J, Peng J F, et al. Experimental and numerical studies of bolted joints subjected to axial excitation[J]. Wear, 2016, 346(1): 66-77.
21	Yang X, Nassar S A, Wu Z, et al. Nonlinear Behavior of preloaded bolted joints under a cyclic separating load[J]. Journal of Pressure Vessel Technology, 2012, 134(1): 011206.
22	闫明, 张义民, 孙志礼, 等. 机械零件相关失效可靠度及灵敏度计算的Monte Carlo方法[J]. 东北大学学报: 自然科学版, 2011, 32(6): 834-837.
	Yan Ming, Zhang Yi-min, Sun Zhi-li, et al. The Monte Carlo method for calculating the reliability and sensitivity of mechanical component related failures[J]. Journal of Northeast University(Natural Science Edition), 2011, 32(6): 834-837.
23	Jiang C, Qiu H, Gao L, et al. Real-time estimation error-guided active learning Kriging method for time-dependent reliability analysis[J]. Applied Mathematical Modelling, 2020, 77(1): 82-98.

相关文章 15

[1]	杨艳,侍玉青,张晓蓉,罗冠炜. 一类多刚性限幅振动系统的动态稳定性分析[J]. 吉林大学学报(工学版), 2023, 53(2): 364-375.
[2]	刘洋. 动臂塔机卸载冲击仿真及试验[J]. 吉林大学学报(工学版), 2022, 52(6): 1292-1300.
[3]	程亚兵,陈璐翔,葛平玉,杨泽宇,曹鹏宇. 双相正时套筒链的动力学仿真分析及磨损失效[J]. 吉林大学学报(工学版), 2022, 52(4): 781-788.
[4]	赵洋,肖洋,孙皓,霍文浩,冯松,廖勇. 基于围道积分的润滑接触齿轮微点蚀损伤特征模拟[J]. 吉林大学学报(工学版), 2022, 52(4): 799-810.
[5]	张朋成,彭斌,张宇波. 基于圆渐开线建立变截面涡旋齿的方法与理论[J]. 吉林大学学报(工学版), 2022, 52(4): 789-798.
[6]	张龙,徐天鹏,王朝兵,易剑昱,甄灿壮. 基于卷积门控循环网络的齿轮箱故障诊断[J]. 吉林大学学报(工学版), 2022, 52(2): 368-376.
[7]	邱继伟,罗海胜. 基于混合不确定性的螺旋锥齿轮结构可靠性分析[J]. 吉林大学学报(工学版), 2022, 52(2): 466-473.
[8]	王立平,朱斌,吴军,陶子寒. 基于贝叶斯网络的盘式刀库故障分析[J]. 吉林大学学报(工学版), 2022, 52(2): 280-287.
[9]	刘璐,周华西,陈传海,龚梦辉,冯虎田,周长光. 基于竞争失效模型的滚珠丝杠副可靠性设计建模[J]. 吉林大学学报(工学版), 2022, 52(2): 458-465.
[10]	宋林,王立平,吴军,关立文,刘知贵. 基于信息物理融合和数字孪生的可靠性分析[J]. 吉林大学学报(工学版), 2022, 52(2): 439-449.
[11]	陈传海,王成功,杨兆军,刘志峰,田海龙. 数控机床可靠性建模研究现状及发展动态分析[J]. 吉林大学学报(工学版), 2022, 52(2): 253-266.
[12]	赵泓荀,杨兆军,陈传海,田海龙,王立平. 考虑参数权重的数控机床电主轴加速试验优化设计[J]. 吉林大学学报(工学版), 2022, 52(2): 409-416.
[13]	郑伟,孙见君,马晨波,於秋萍,张玉言,牛韬. 汽车轮毂加工夹具的研究现状及展望[J]. 吉林大学学报(工学版), 2022, 52(1): 25-36.
[14]	樊学平,杨光红,尚志鹏,赵小雄,肖青凯,刘月飞. 考虑适用性的大跨桥梁主梁动态可靠性融合预测[J]. 吉林大学学报(工学版), 2022, 52(1): 144-153.
[15]	李国发,陈泽权,何佳龙. 新型结构可靠性分析自适应加点策略[J]. 吉林大学学报(工学版), 2021, 51(6): 1975-1981.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

参数	螺栓	螺母
公称直径/mm	10	10
牙型角/（°）	60	60
螺距/mm	1.5	1.5
弹性模量/GPa	210	210
泊松比	0.3	0.3
密度/（kg·m^-2）	7850	7850

夹紧力/N	仿真值	组别				平均值
夹紧力/N	仿真值	1	2	3	4	平均值
50	3.18	2.87	3.35	3.83	3.23	3.32
100	6.34	6.23	5.27	6.71	6.48	6.17
150	9.52	10.54	9.58	10.06	9.89	10.02
200	12.59	13.41	11.50	12.45	12.93	12.57
250	15.84	14.85	15.33	16.29	16.77	15.81
300	18.99	19.64	18.20	18.68	17.72	18.56
350	22.14	22.99	23.47	20.12	22.04	22.16
400	25.24	24.91	26.35	24.43	23.95	24.91
450	28.55	29.22	28.74	26.83	25.39	27.55
500	31.52	30.18	31.14	32.57	34.49	32.10

夹紧力/N	有限元应力值/MPa	各项夹紧力下对应的实验应力值/MPa
50	0.634	0.664
100	1.255	1.234
150	1.904	2.004
200	2.523	2.514
250	3.171	3.162
300	3.797	3.712
350	4.419	4.432
400	5.066	4.982
450	5.593	5.510
500	6.352	6.420

螺栓参数	数值	分布	变异系数
螺栓大径D/mm	10	正态分布	0.002
螺栓的牙型角α/（°）	60	正态分布	0.005
螺栓的螺距p/mm	1.5	正态分布	0.005
弹性模量E_m/GPa	210	正态分布	0.05
密度ρ/（kg·m^-3）	7850	正态分布	0.05
泊松比μ₀	0.3	正态分布	0.05