单圆管CFST拱桥面外弹性分支屈曲临界荷载计算方法

doi:10.13229/j.cnki.jdxbgxb.20221582

吉林大学学报(工学版) ›› 2024, Vol. 54 ›› Issue (10): 2930-2940.doi: 10.13229/j.cnki.jdxbgxb.20221582

• 交通运输工程·土木工程 • 上一篇

单圆管CFST拱桥面外弹性分支屈曲临界荷载计算方法

黄卿维^1,²(),吴庆雄^1,²(),陈宝春^2,³,陈康明^1,²,叶智威¹

^1.福州大学土木工程学院，福州 350108
^2.福州大学可持续与创新桥梁福建省高校工程研究中心，福州 350108
^3.福建工程学院土木工程学院，福州 350118

收稿日期:2022-12-10 出版日期:2024-10-01 发布日期:2024-11-22
通讯作者: 吴庆雄 E-mail:huangqingwei@fzu.edu.cn;3390351686@qq.com
作者简介:黄卿维（1982-），男，副研究员，博士. 研究方向：大跨度桥梁与组合结构. E-mail： huangqingwei@fzu.edu.cn
基金资助:
国家重点研发计划项目(2017YFE0130300);国家自然科学基金项目(52078137);福建省自然科学基金杰青项目(2019J06009)

Calculation method of out-of-plane elastic stability bearing capacity for concrete-filled steel tubular arch bridges with circular tube ribs

Qing-wei HUANG^1,²(),Qing-xiong WU^1,²(),Bao-chun CHEN^2,³,Kang-ming CHEN^1,²,Zhi-wei YE¹

^1.College of Civil Engineering，Fuzhou University，Fuzhou 350108，China
^2.Sustainable and Innovative Bridge Engineering Research Center of Fujian Province University，Fuzhou University，Fuzhou 350108，China
^3.College of Civil Engineering，Fujian University of Technology，Fuzhou 350118，China

Received:2022-12-10 Online:2024-10-01 Published:2024-11-22
Contact: Qing-xiong WU E-mail:huangqingwei@fzu.edu.cn;3390351686@qq.com

摘要/Abstract

摘要：

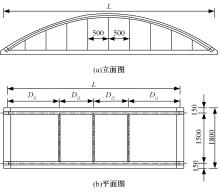
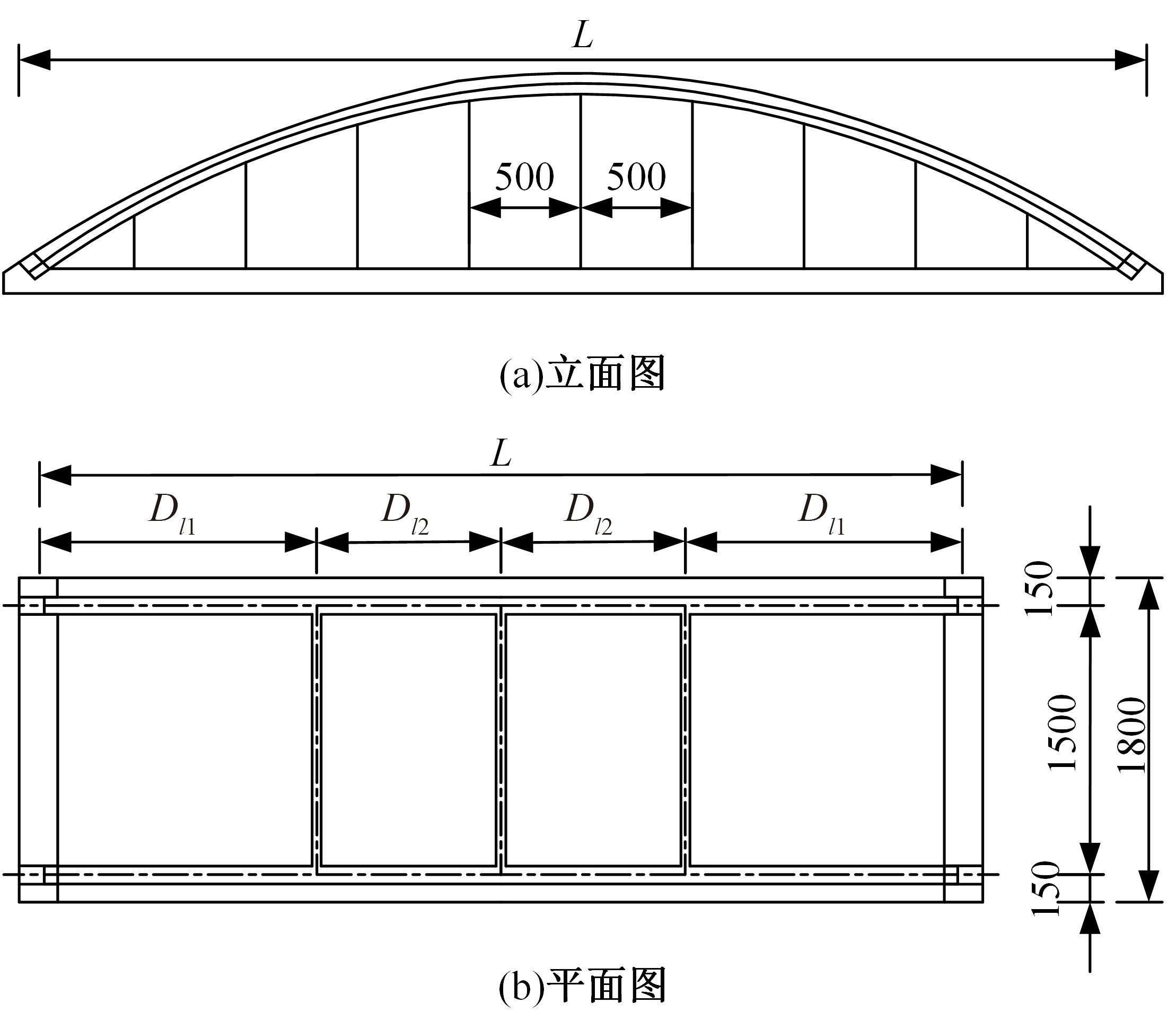
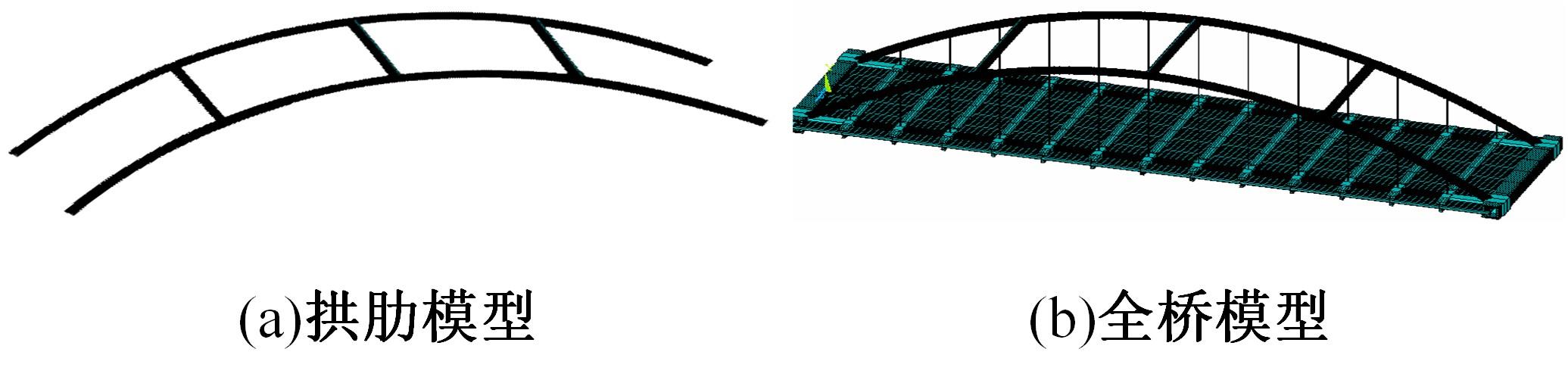
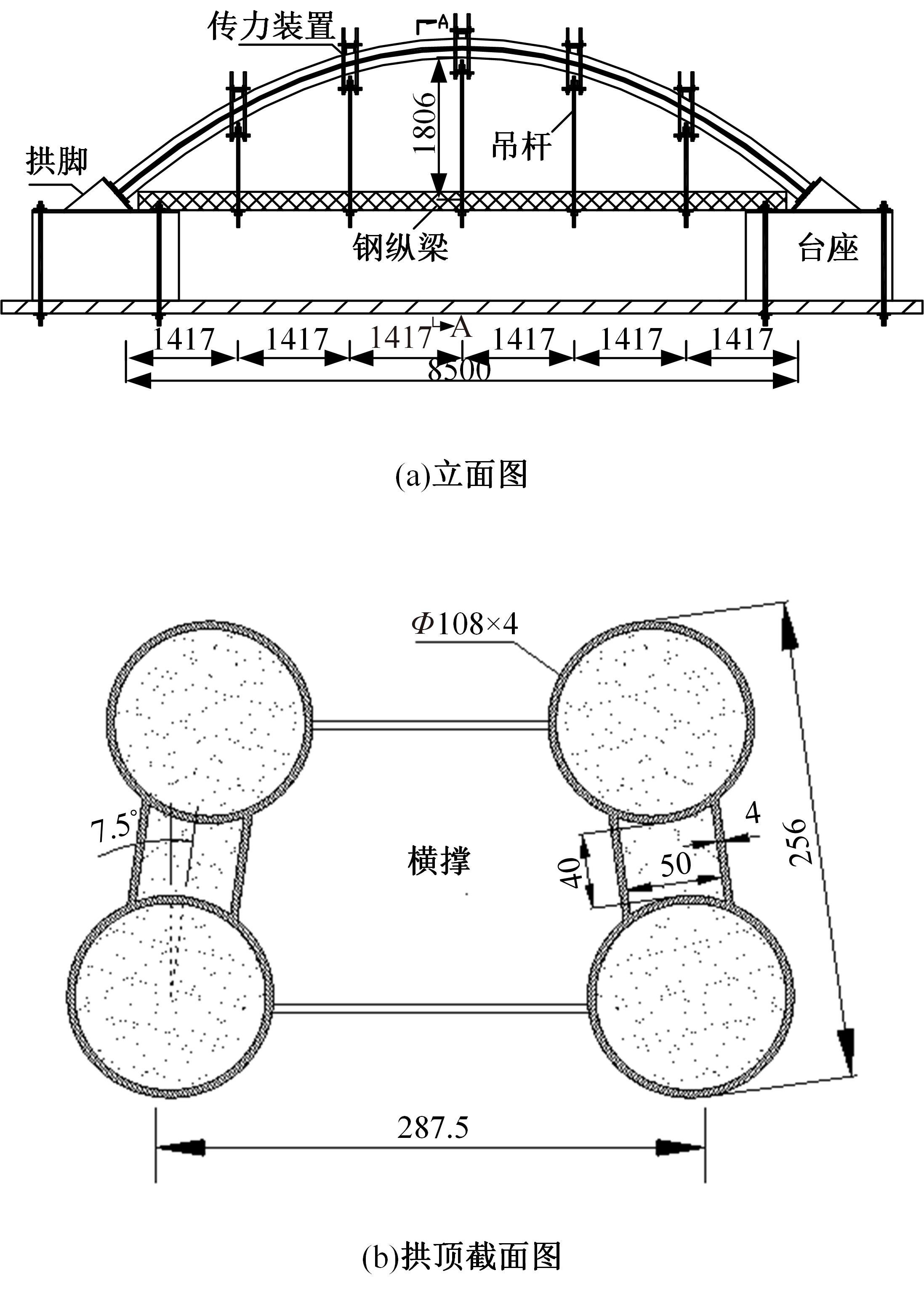
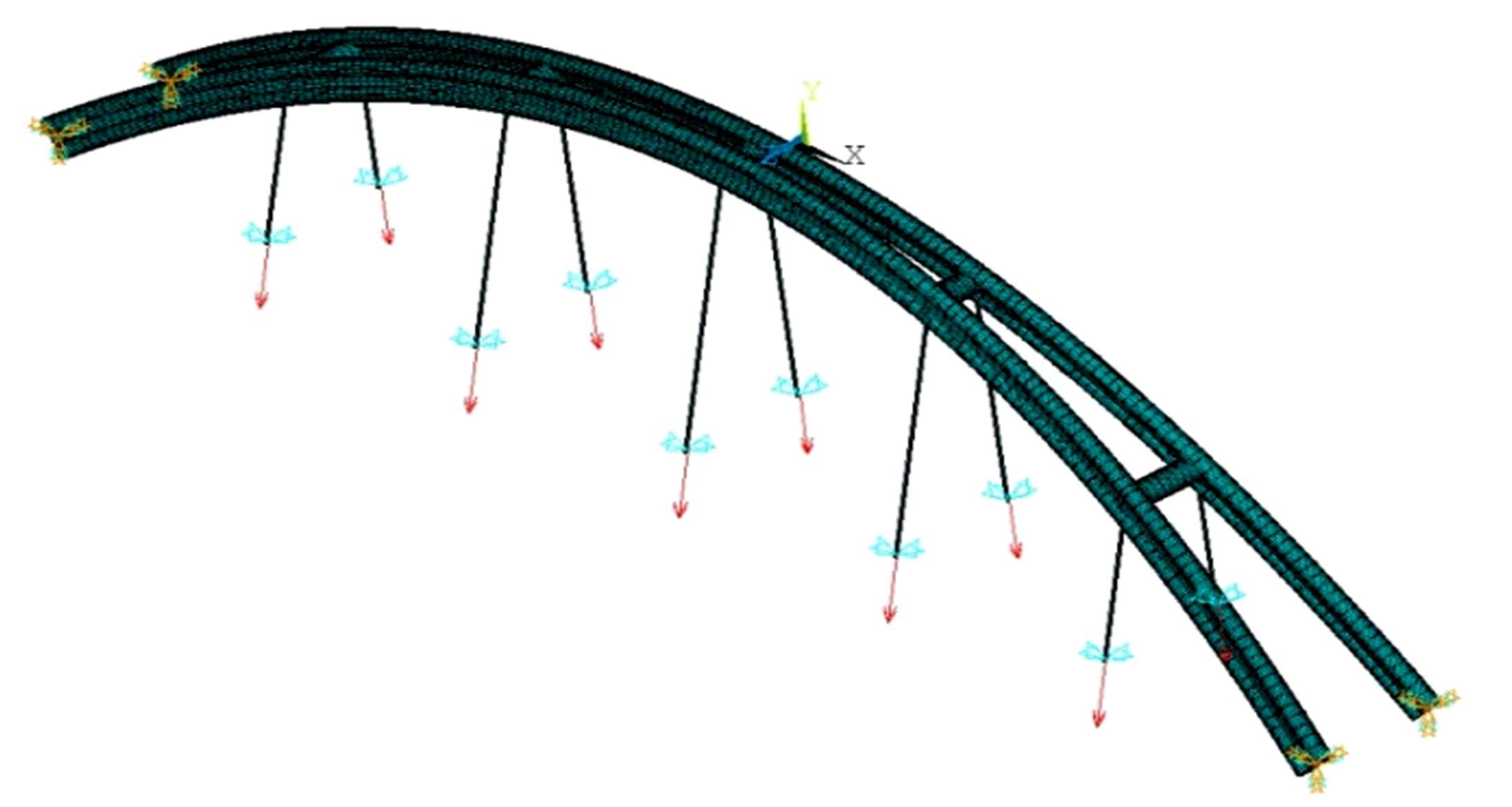
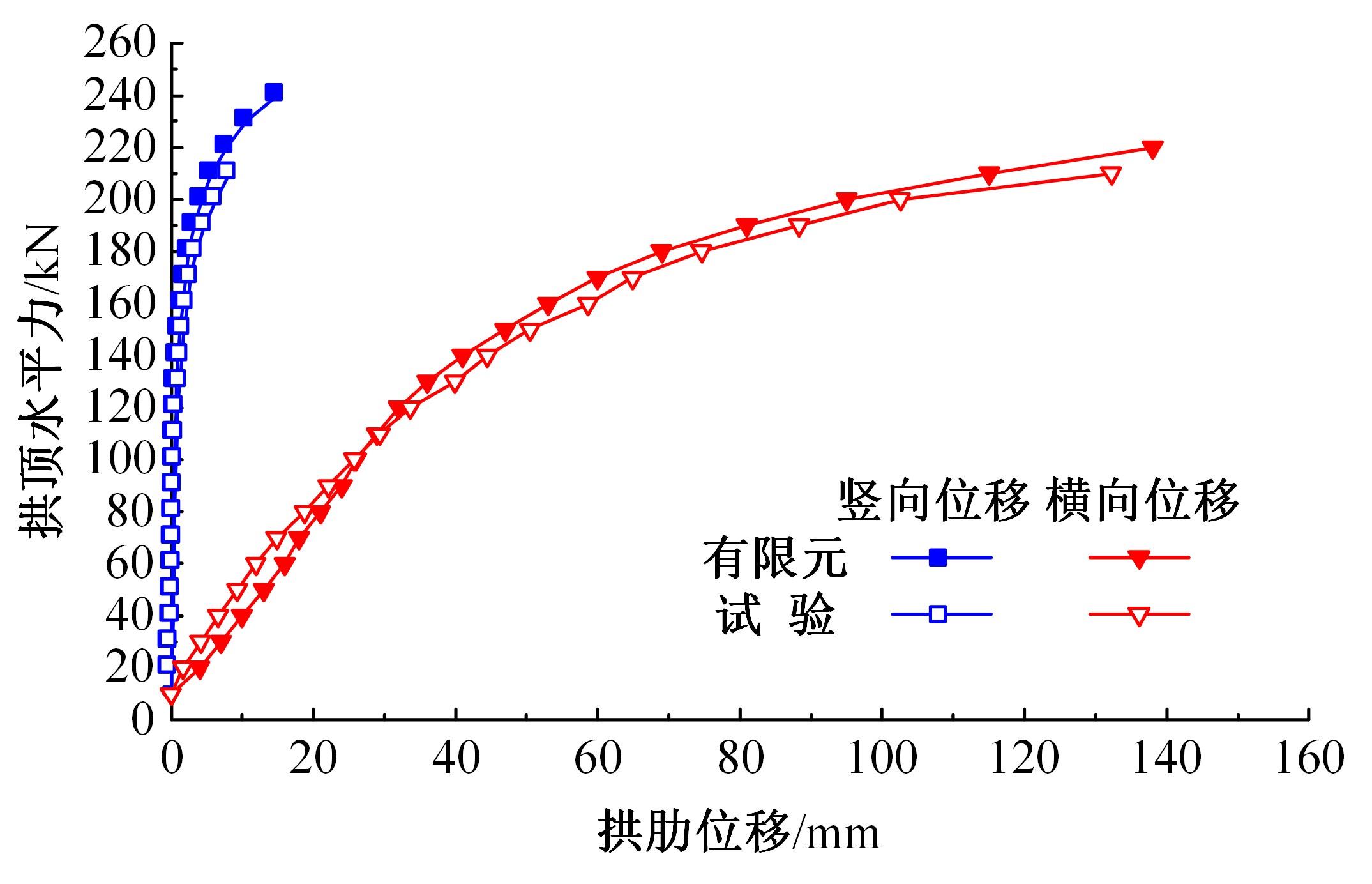
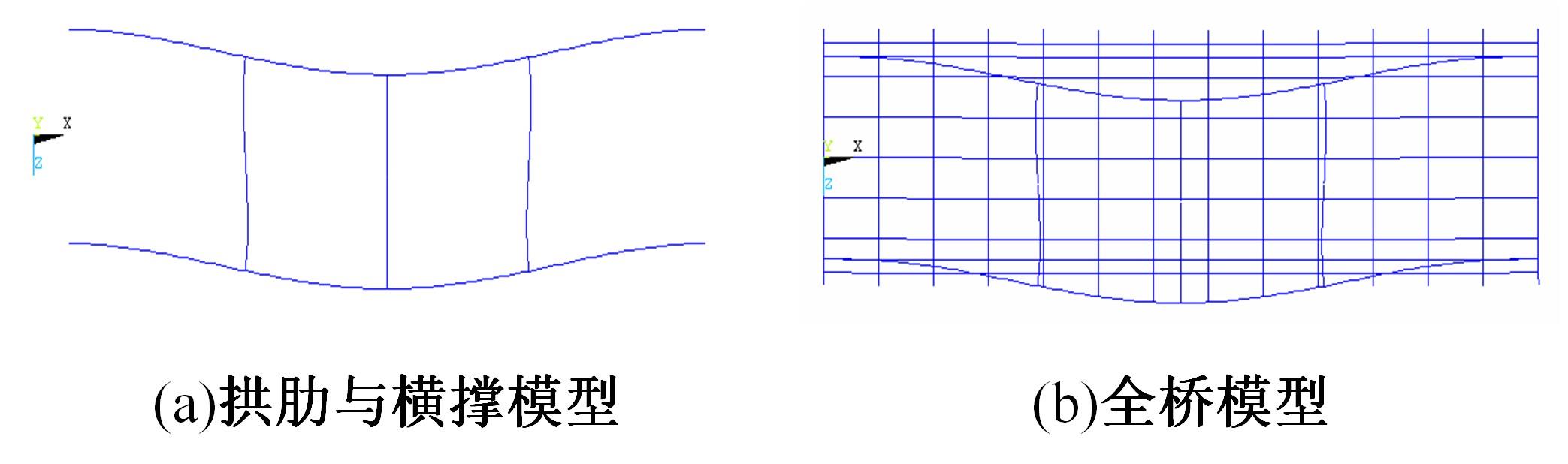
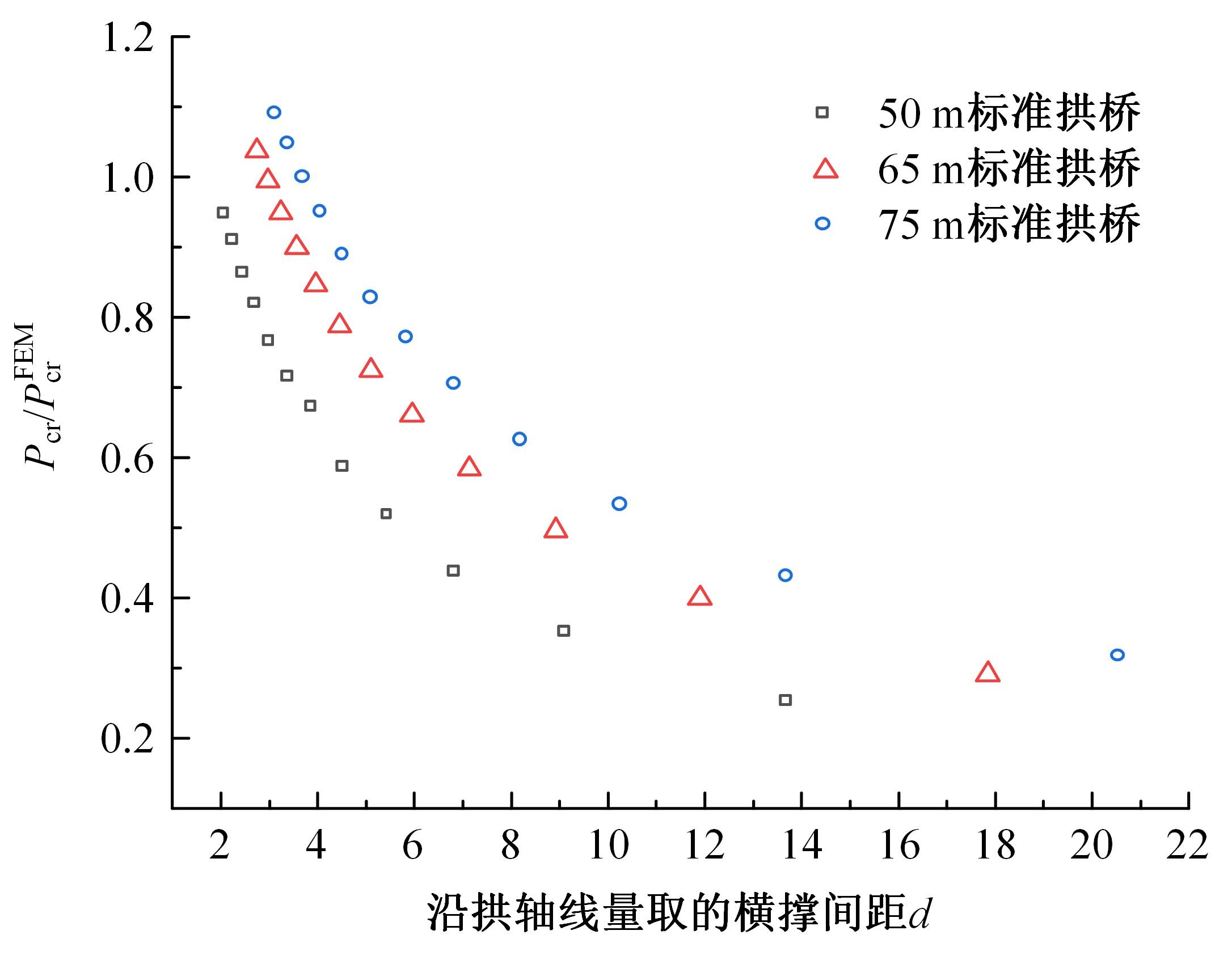
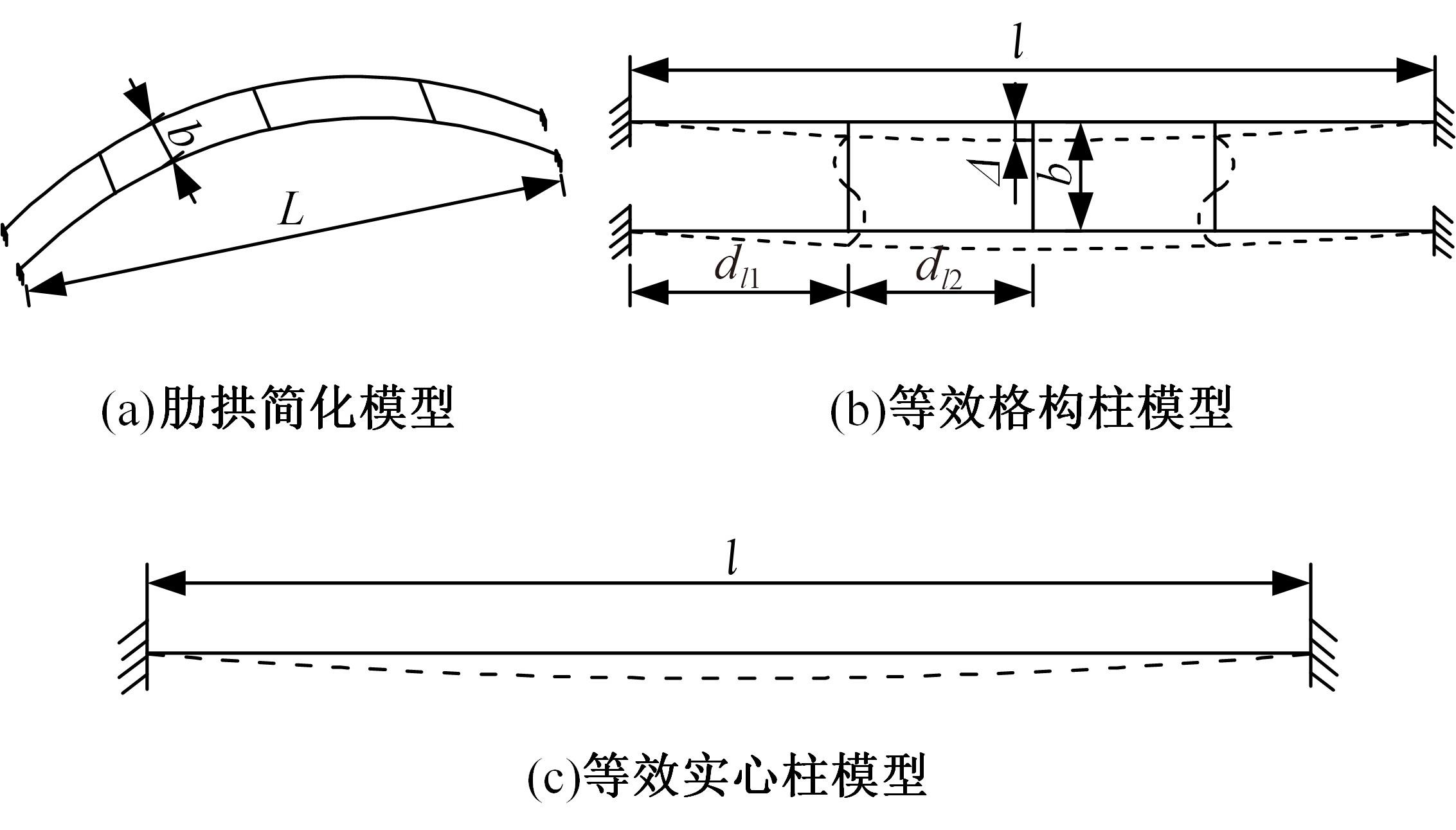
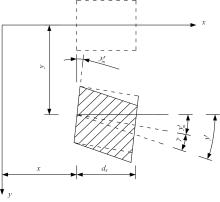
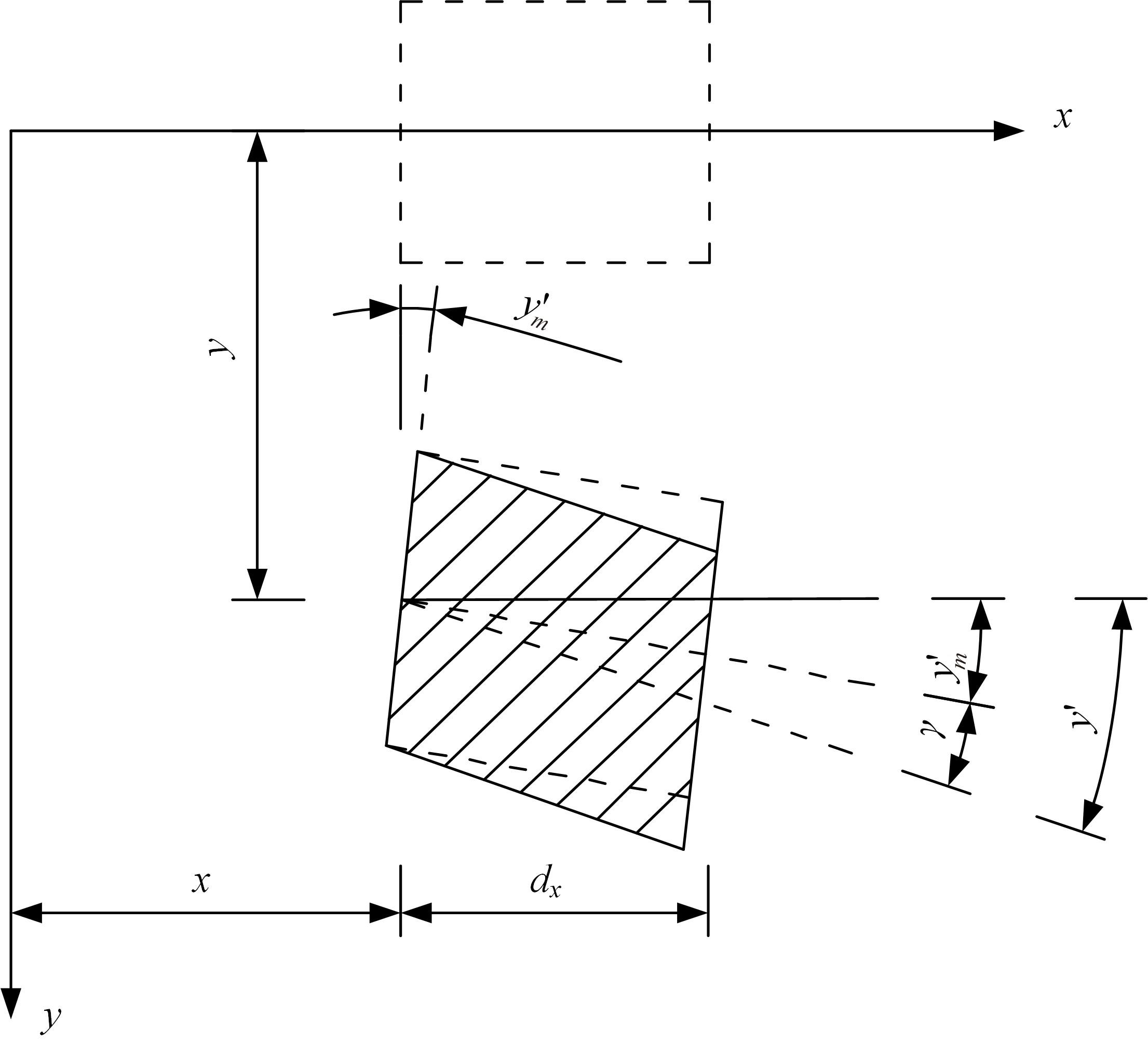
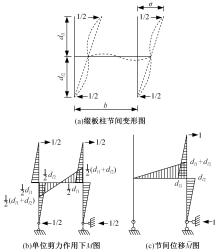
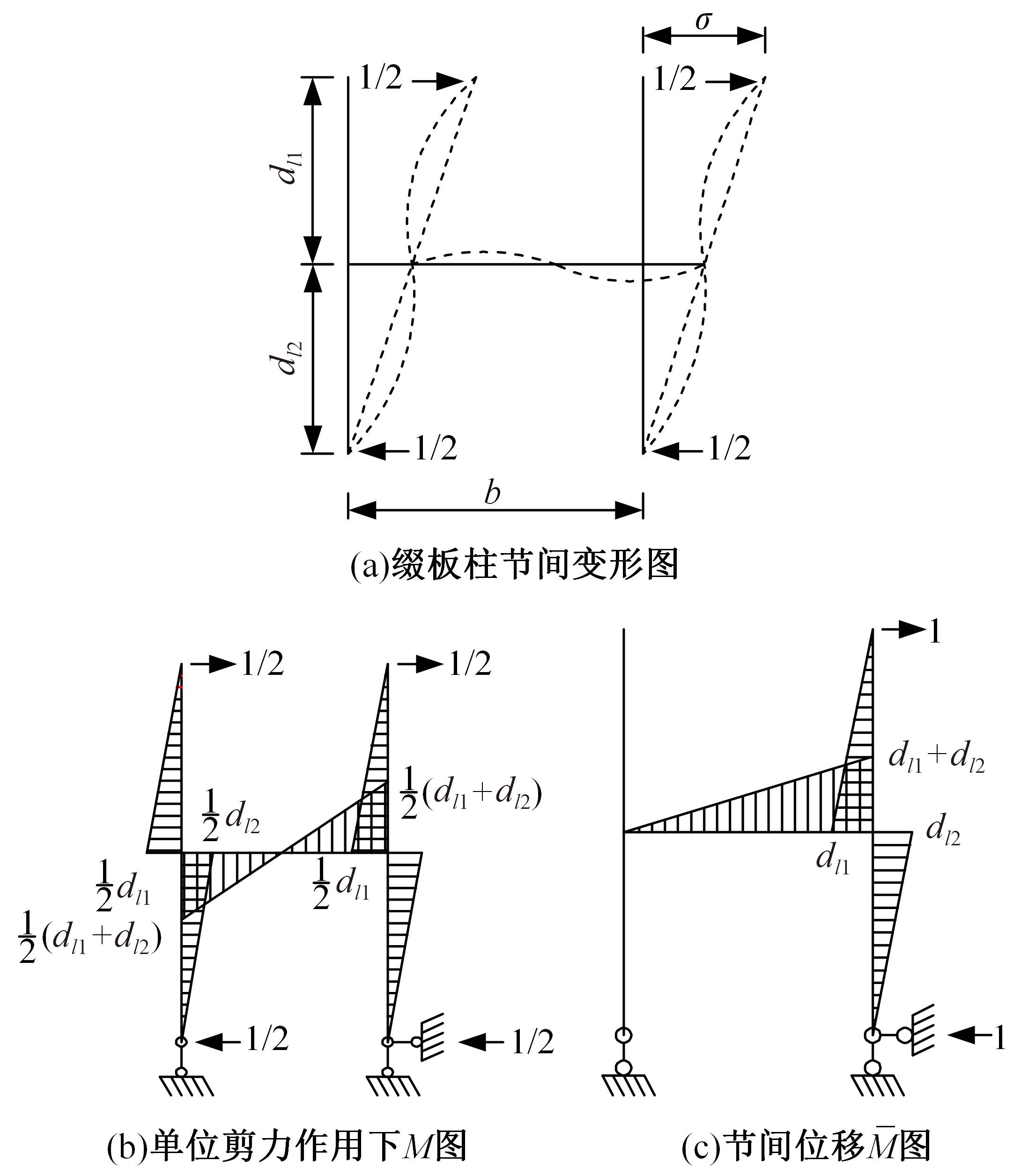
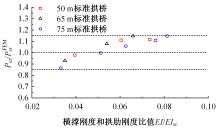
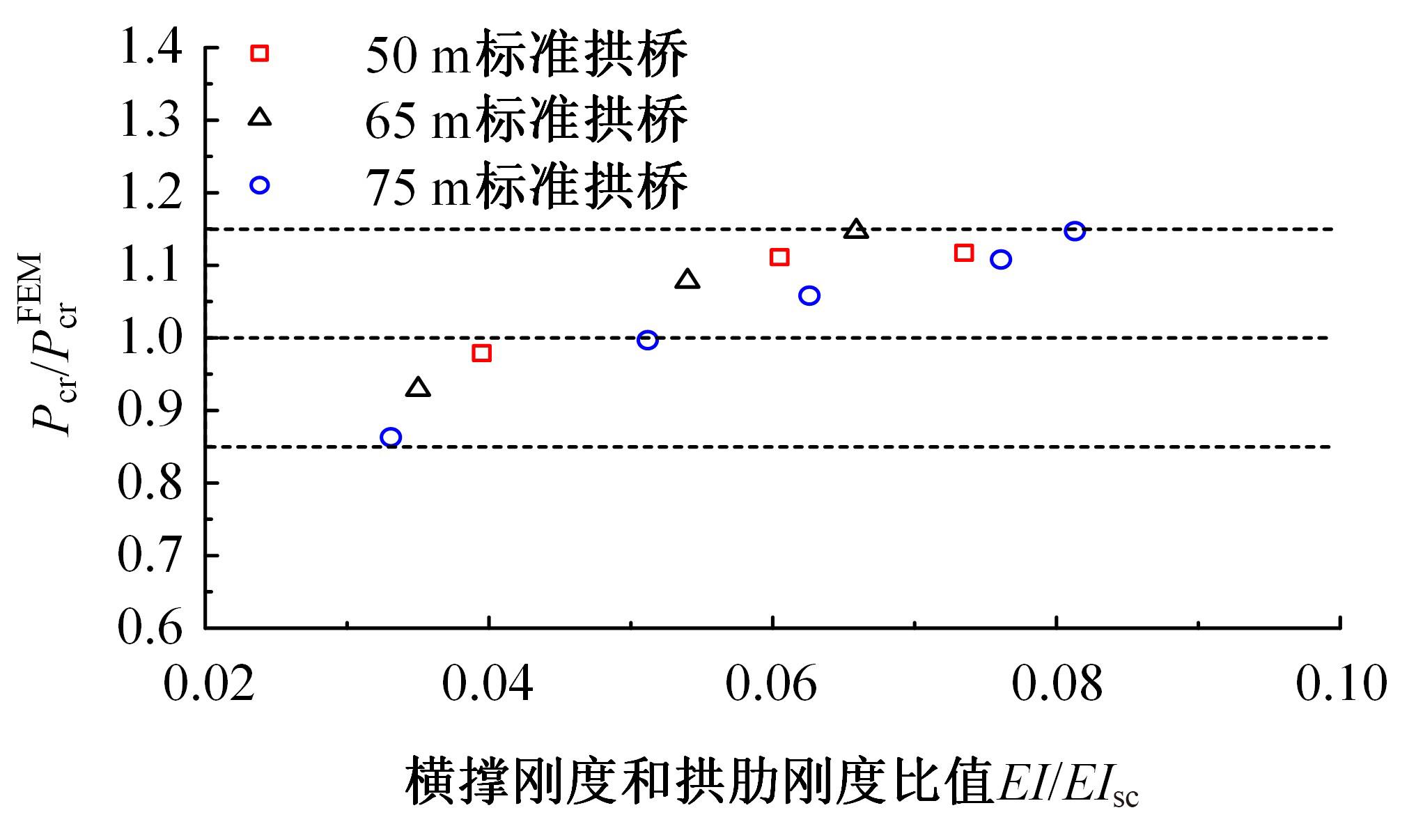
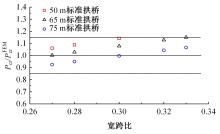
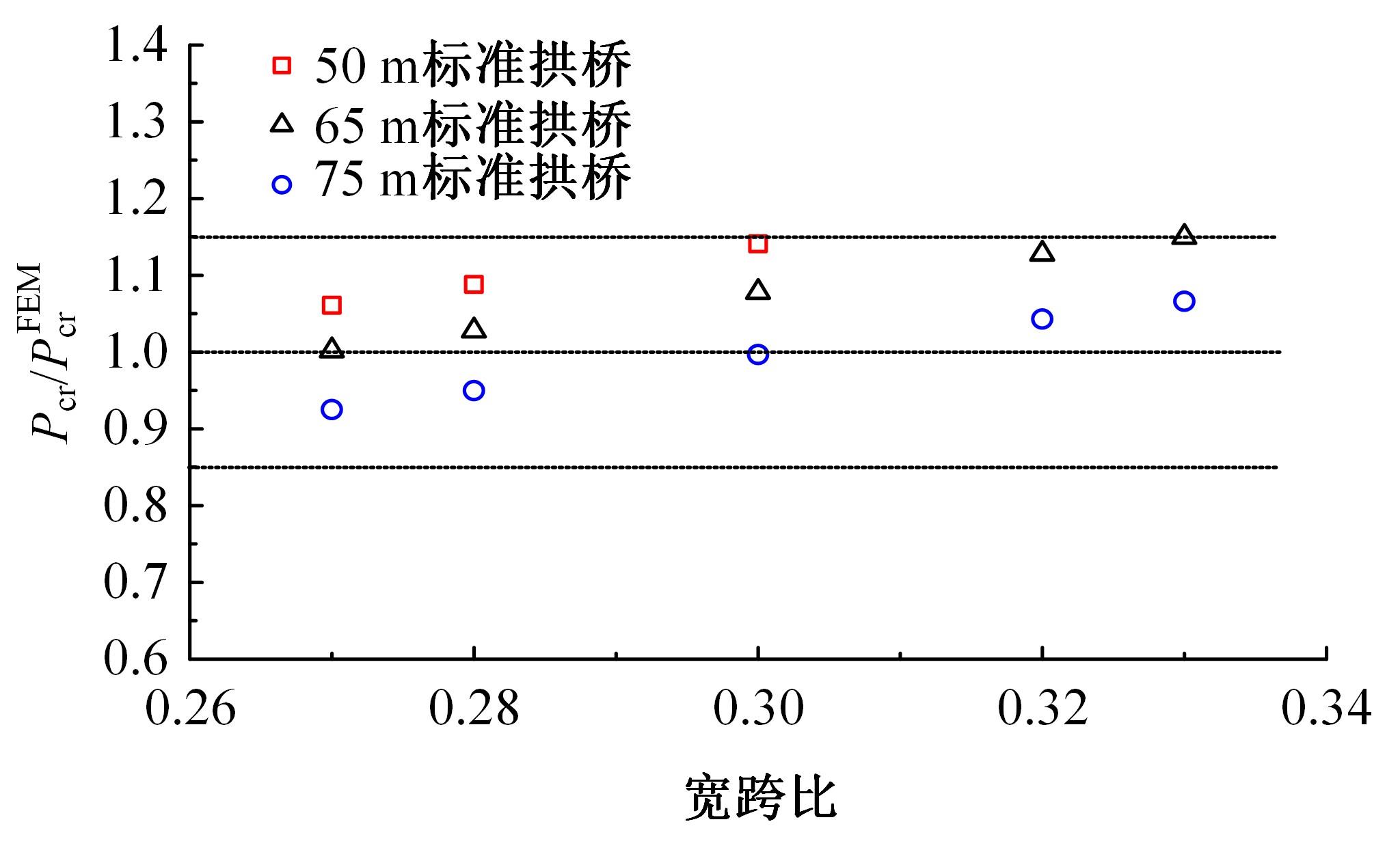
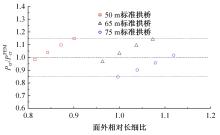
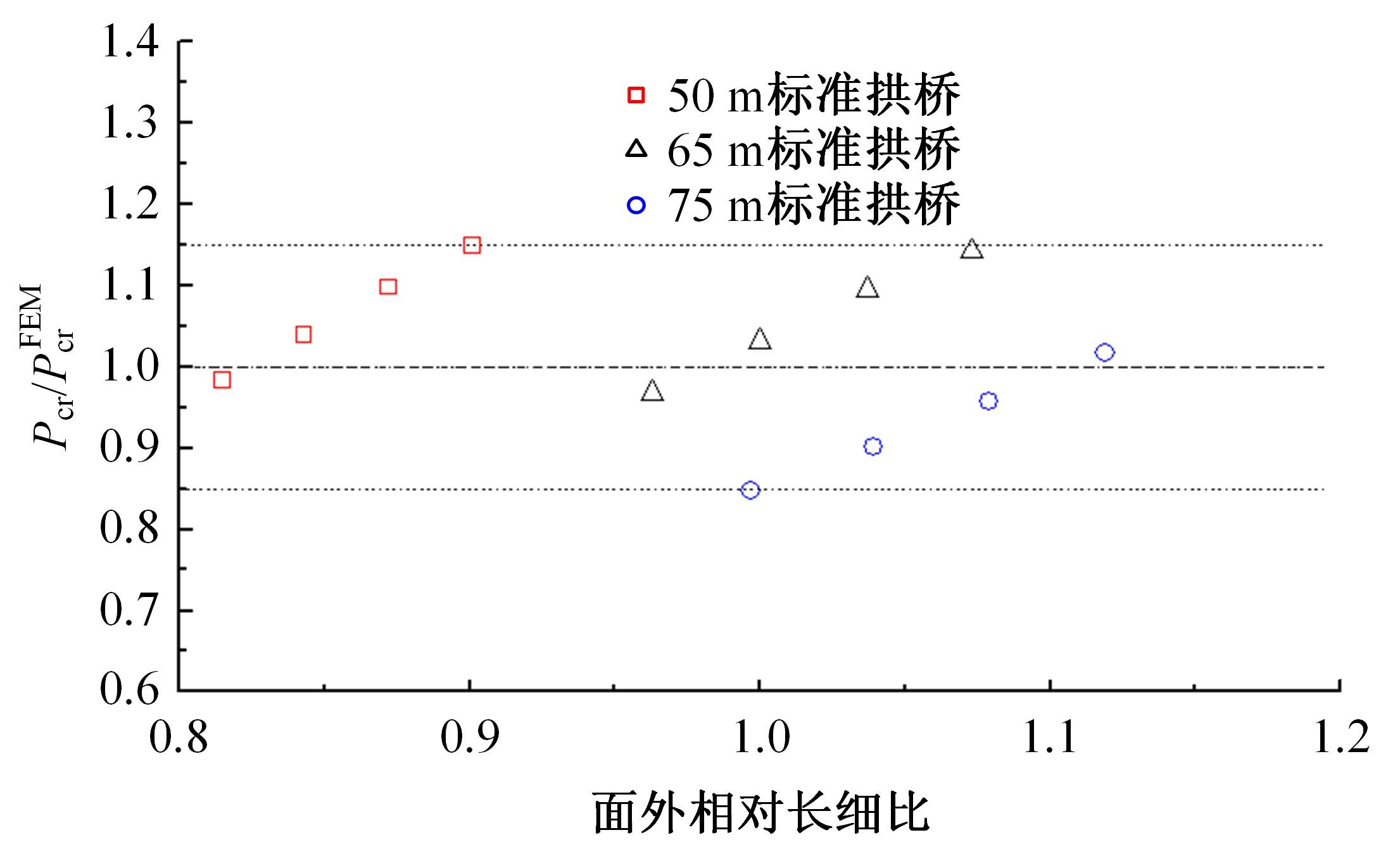
单圆管钢管混凝土（CFST）拱桥常采用稀疏的横撑布置形式，面外失稳时具有较大的剪切变形，不适合采用现有基于不考虑剪切变形假定的计算方法。本文以缀板稀疏布置的格构柱为研究对象，推导得到考虑剪切变形后格构柱弹性分支屈曲临界荷载计算公式，并以格构柱弹性分支屈曲临界荷载计算公式为基础，采用等效梁柱法推导得到考虑剪切变形的单圆管钢管混凝土拱桥面外弹性分支屈曲临界荷载计算公式。开展了单圆管钢管混凝土标准拱桥有限元参数分析，并将有限元分析结果与考虑和不考虑剪切变形计算公式、现有规范与参考文献推荐计算公式的计算结果进行对比分析。研究结果表明：在工程常用的结构尺寸范围内，现有规范和文献推荐公式计算结果比有限元计算结果小了1个数量级，不适用于计算单圆管钢管混凝土拱桥面外弹性分支屈曲临界荷载。本文提出的考虑剪切变形的单圆管钢管混凝土拱桥面外弹性分支屈曲临界荷载计算公式与有限元计算结果的误差在15%之内，具有较大的精度提升和较好的适用性。

关键词: 桥梁工程, 钢管混凝土拱桥, 单圆管, 面外, 弹性稳定, 极限承载力算法

Abstract:

The concrete-filled steel tubular （CFST） arch bridges with circular tube ribs usually adopt the sparsely arranged transverse braces， which have a large shear deformation in the out-of-plane instability， it is not suitable to use the existing calculation method based on the assumption that shear deformation is not considered. Taking the lattice columns with sparsely battened plates as the research object， the calculation formula of elastic stability bearing capacity of lattice columns considering the shear deformation is derived. Based on the calculation formula of elastic stability bearing capacity of lattice column and by employing the equivalent beam-column method， the calculation formula of out-of-plane elastic stability bearing capacity considering shear deformation for CFST arch bridge with circular tube ribs is proposed. The parameter analysis on the standard CFST arch bridges with circular tube ribs are carried out by finite element （FE） method， the results are compared with the calculation results according to formulas considering and without considering shear deformations， and formulas recommended by the existing codes and references. The results of research show that in the scope of structure dimensions commonly used in engineering， the results obtained by recommended formulas in existing codes and references are one order of magnitude smaller than those obtained by finite element method， they are not suitable for the calculation of out-of-plane elastic stability bearing capacity of CFST arch bridge with circular tube ribs. The error between FE analysis and proposed calculation formula of out-of-plane elastic stability bearing capacity considering shear deformation for CFST arch bridge is within 15%， which has a large precision improvement and good applicability.

Key words: bridge engineering, concrete-filled steel tube arch bridge, single circular tube, out-of-plane, elastic stability, bearing capacity calculation

中图分类号:

TU391

黄卿维,吴庆雄,陈宝春,陈康明,叶智威. 单圆管CFST拱桥面外弹性分支屈曲临界荷载计算方法[J]. 吉林大学学报(工学版), 2024, 54(10): 2930-2940.

Qing-wei HUANG,Qing-xiong WU,Bao-chun CHEN,Kang-ming CHEN,Zhi-wei YE. Calculation method of out-of-plane elastic stability bearing capacity for concrete-filled steel tubular arch bridges with circular tube ribs[J]. Journal of Jilin University(Engineering and Technology Edition), 2024, 54(10): 2930-2940.

图/表 18

图1

表1

标准拱桥尺寸汇总表"

跨径/m	D $l 1$ /m	D $l 2$ /m	矢跨比f/l	钢管管径/mm	钢管壁厚/mm	横撑管径/mm	横撑壁厚/mm
50	15	10	1/5	850	16	425	16
65	19.5	13	1/5	1000	16	500	16
75	22.5	15	1/5	1100	16	550	16

表1

图2

图3

图4

图5

图6

图7

表2

50 m标准拱桥弹性分支屈曲临界荷载计算结果汇总"

项目		计算公式
项目		考虑剪切变形	不考虑剪切变形	JTG 3362—2018	吴恒立
剪切系数μ		770.39	770.39	—	—
剪切影响系数α₀		1.140×10^-2	1.315×10^-4	1.313×10^-4	1.319×10^-4
弹性分支屈曲临界荷载P_cr/N		5.405×10⁷	4.986×10⁶	4.979×10⁶	5.001×10⁶
有限元结果P $c r F E M$ /N	拱肋模型	4.656×10⁷
有限元结果P $c r F E M$ /N	全桥模型	4.735×10⁷

表2

图8

图9

图10

图11

图12

图13

图14

图15

图16

参考文献 23

1	陈宝春. 钢管混凝土拱桥[M].3版. 北京: 人民交通出版社, 2016.
2	陈宝春, 韦建刚, 周俊, 等. 我国钢管混凝土拱桥应用现状与展望[J]. 土木工程学报, 2017, 50(6): 50-61.
	Chen Bao-chun, Wei Jian-gang, Zhou Jun, et al. Application of concrete-filled steel tube arch bridges in China: current status and prospects[J]. China Civil Engineering Journal, 2017, 50(6): 50-61.
3	崔军, 王景波, 孙炳楠. 大跨度钢管混凝土拱桥非线性稳定性分析[J]. 哈尔滨工业大学学报, 2003, 35(7): 876-878.
	Cui Jun, Wang Jing-bo, Sun Bing-nan. Nonlinear buckling analysis for large span concrete filled steel tube arc bridge[J]. Journal of Harbin Institute of Technology, 2003, 35(7): 876-878.
4	邵旭东, 何广. 800m级钢-UHPC组合桁式拱桥概念设计与可行性研究[J]. 中国公路学报, 2020, 33(2): 73-82.
	Shao Xu-dong, He Guang. Conceptual design and feasibility study of an 800 m scale steel-UHPC composite truss arch bridge[J]. China Journal of Highway and Transport, 2020, 33(2): 73-82.
5	陈宝春, 刘君平. 世界拱桥建设与技术发展综述[J]. 交通运输工程学报, 2020, 20(1): 27-41.
	Chen Bao-chun, Liu Jun-ping. Review of construction and technology development of arch bridges in the world[J]. Journal of Traffic and Transportation Engineering, 2020, 20(1): 27-41.
6	施洲, 张勇, 张育智, 等. 大跨度铁路下承式钢桁梁柔性拱桥稳定性研究[J].中国铁道科学,2019,40(4): 52-58.
	Shi Zhou, Zhang Yong, Zhang Yu-zhi, et al. Study on stability of long-span railway through bridge with steel truss girder and flexible arch[J]. China Railway Science, 2019, 40(4): 52-58.
7	谢肖礼, 覃霞, 欧阳平, 等. 提高拱梁固结拱桥刚度的有效方法[J]. 同济大学学报:自然科学版, 2019, 47(6): 747-753.
	Xie Xiao-li, Qin Xia, Yang-ping Ou, et al. An effective method to improve the stiffness of arch-beam fixed arch bridges[J]. Journal of Tongji University (Natural Science), 2019, 47(6): 747-753.
8	耿悦, 周昌杰, 王玉银, 等. 抛物线形钢管混凝土无铰拱出平面稳定性能研究[J]. 建筑结构学报, 2015, 36(): 114-119.
	Geng Yue, Zhou Chang-jie, Wang Yu-yin, et al. Out-of-plane buckling behavior of slender parabolic concrete-filled steel tubular arches with fixed ends[J]. Journal of Building Structures, 2015, 36(Sup.1): 114-119.
9	陈宝春, 秦泽豹. 钢管混凝土(单圆管)肋拱面内极限承载力计算的等效梁柱法[J]. 铁道学报, 2006(6): 99-104.
	Chen Bao-chun, Qin Ze-bao. Equivalent beam-column method for calculation of the ultimate load-carrying capacity of concrete filled steel tube(single) arch under in-plane loads[J]. Journal of the China Railway Society, 2006(6): 99-104.
10	陈宝春, 盛叶. 钢管混凝土哑铃形拱面内极限承载力研究[J]. 工程力学, 2009, 26(9): 94-104.
	Chen Bao-chun, Sheng Ye. Research on load-carrying capacity of concrete filled steel tubular dumbbell shaped rib arch under in-plane loads[J]. Engineering Mechanics, 2009, 26(9): 94-104.
11	高婧, 陈宝春. 波形钢腹板钢管混凝土模型拱面内稳定承载力试验研究[J]. 工程力学, 2010, 27(3): 91-100.
	Gao Jing, Chen Bao-chun. Experimental study on in-plane ultimate load-carrying capacity of cfst arches with corrugated steel webs[J]. Engineering Mechanics, 2010, 27(3): 91-100.
12	何晓升. 压弯状态下钢管混凝土圆弧拱的工作机理与应用研究[D]. 北京: 中国矿业大学力学与土木工程学院, 2016.
	He Xiao-sheng. Research on application and behavior of concrete-filled steel tubes arch under bending state[D]. Beijing: School of Mechanical and Civil Engineering, China University of Mining and Technology, 2016.
13	Liu C Y, Wang Y Y, Wu X R, et al. In-plane stability of fixed concrete-filled steel tubular parabolic arches under combined bending and compression[J]. Journal of Bridge Engineering, 2017, 22(2): 1-15.
14	刘福忠, 李广奇, 郭保林. 单圆管钢管混凝土拱桥面内稳定参数分析[J]. 山东交通科技, 2019(4): 55-57.
	Liu Fu-zhong, Li Guang-qi, Guo Bao-lin. Analysis of in-plane stability parameters of single tube CFST arch bridge[J]. Journal of Shandong Transportation Technology, 2019(4): 55-57.
15	吴恒立. 拱式体系的稳定计算[M]. 北京: 人民交通出版社, 1979.
16	陈宝春, 韦建刚, 林嘉阳. 钢管混凝土(单圆管)单肋拱空间受力试验研究[J]. 工程力学, 2006, 23(5): 99-106.
	Chen Bao-chun, Wei Jian-gang, Lin Jia-yang. Experimental study on concrete filled steel tubular (sinle) arch with one rib under spatial loads[J]. Engineering Mechanics, 2006, 23(5): 99-106.
17	李晓辉. 钢管混凝土实肋拱面外稳定性能研究[D]. 福州: 福州大学土木工程学院, 2011.
	Li Xiao-hui. Research on the out-of plane stability of cfst solid rib arches[D]. Fuzhou: College of Civil Engineering, Fuzhou University, 2011.
18	梁勇. 钢管混凝土抛物线拱平面外稳定性能研究[D]. 哈尔滨: 哈尔滨工业大学土木工程学院, 2016.
	Liang Yong. Out-of-plane stability of parabolic concrete-filled steel tubular arches[D]. Harbin: College of Civil Engineering,Harbin Institute of Technology, 2016.
19	宋福春. 钢管混凝土桁肋拱桥面外稳定性研究[D]. 福州: 福州大学土木工程学院, 2009.
	Song Fu-chun. Research on external stability of steel pipe concrete truss arch bridge[D]. Fuzhou: College of Civil Engineering, Fuzhou University, 2009.
20	. 公路钢筋混凝土及预应力混凝土桥涵设计规范 [S]. 北京: 人民交通出版社, 2018.
21	Lothers J E. Elastic restraint equation for semi-rigid connections[J]. ASCE, 1951, 116: 480-502.
22	Maugh L C. Statically Indeterminate Structures[M].2nd ed.New York:John Wiley and Sons, Inc., 1964.
23	王媛, 叶智威, 吴庆雄. 钢管混凝土单圆管标准拱桥面外稳定性有限元分析方法研究[J]. 世界桥梁, 2015, 43(3): 38-42.
	Wang Yuan, Ye Zhi-wei, Wu Qing-xiong. Out-of-plane stability analysis for typical concrete-filled single steel circular tube arch bridge by finite element method[J]. World Bridges, 2015, 43(3): 38-42.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

[1]	孙永新,蔺鹏臻,杨子江,冀伟. 考虑黏结-滑移效应的UHPC梁裂缝宽度计算方法[J]. 吉林大学学报(工学版), 2024, 54(9): 2600-2608.
[2]	薛宇欣,周勇军,王业路,范凯翔,赵煜. 基于悬锤系统的简支梁桥冲击系数测试方法适用性[J]. 吉林大学学报(工学版), 2024, 54(9): 2557-2567.
[3]	郭雪莲,韩万水,王涛,周恺,张修石,张书颖. 大件车通行弯桥抗倾覆稳定安全系数评估方法[J]. 吉林大学学报(工学版), 2024, 54(8): 2229-2237.
[4]	肖林,魏欢博,卫星,康志锐. 钢混组合梁栓钉锈胀下混凝土板开裂行为数值分析[J]. 吉林大学学报(工学版), 2024, 54(7): 1958-1965.
[5]	张春雷,邵长宇,苏庆田,戴昌源. 球扁钢肋钢纤维混凝土组合桥面板正弯矩受力性能试验[J]. 吉林大学学报(工学版), 2024, 54(6): 1634-1642.
[6]	张彦玲,贾云飞,贾晓远,郑旺,李运生. 装配式小箱梁桥内力横向分布系数建议公式[J]. 吉林大学学报(工学版), 2024, 54(6): 1688-1700.
[7]	黄汉辉,陈康明,吴庆雄. 钢管混凝土桁式弦杆组合连续梁抗弯性能[J]. 吉林大学学报(工学版), 2024, 54(6): 1665-1676.
[8]	邵长江,崔皓蒙,漆启明,庄卫林. 近断层大跨RC轻柔拱桥纵向阻尼器减震研究[J]. 吉林大学学报(工学版), 2024, 54(5): 1355-1367.
[9]	赵秋,陈鹏,赵煜炜,余澳. 台后设置拱形结构的无缝桥梁整体受力性能[J]. 吉林大学学报(工学版), 2024, 54(4): 1016-1027.
[10]	张洪,朱志伟,胡天宇,龚燕峰,周建庭. 基于改进YOLOv5s的桥梁螺栓缺陷识别方法[J]. 吉林大学学报(工学版), 2024, 54(3): 749-760.
[11]	韩智强,谢刚,卓亚娟,骆佐龙,李华腾. 基于车轮-桥面相干激励的大跨连续梁桥振动响应[J]. 吉林大学学报(工学版), 2024, 54(2): 436-444.
[12]	杨国俊,齐亚辉,石秀名. 基于数字图像技术的桥梁裂缝检测综述[J]. 吉林大学学报(工学版), 2024, 54(2): 313-332.
[13]	张协力,吴冲,苏庆田. 压型钢板-混凝土组合桥面板极限承载力试验[J]. 吉林大学学报(工学版), 2024, 54(10): 2870-2883.
[14]	谭国金,欧吉,艾永明,杨润超. 基于改进DeepLabv3+模型的桥梁裂缝图像分割方法[J]. 吉林大学学报(工学版), 2024, 54(1): 173-179.
[15]	龙关旭,张修石,辛公锋,王涛,杨干. 融合机器视觉的桥梁动态称重方法[J]. 吉林大学学报(工学版), 2024, 54(1): 188-197.

单圆管CFST拱桥面外弹性分支屈曲临界荷载计算方法

Calculation method of out-of-plane elastic stability bearing capacity for concrete-filled steel tubular arch bridges with circular tube ribs

RICH HTML

PDF (PC)

摘要/Abstract

引用本文

使用本文

图/表 18

参考文献 23

相关文章 15

Metrics

本文评价

推荐阅读 0