温度和车辆作用下梁式桥梁结构固有频率分析方法

doi:10.13229/j.cnki.jdxbgxb.20230263

摘要/Abstract

摘要：

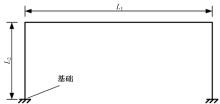
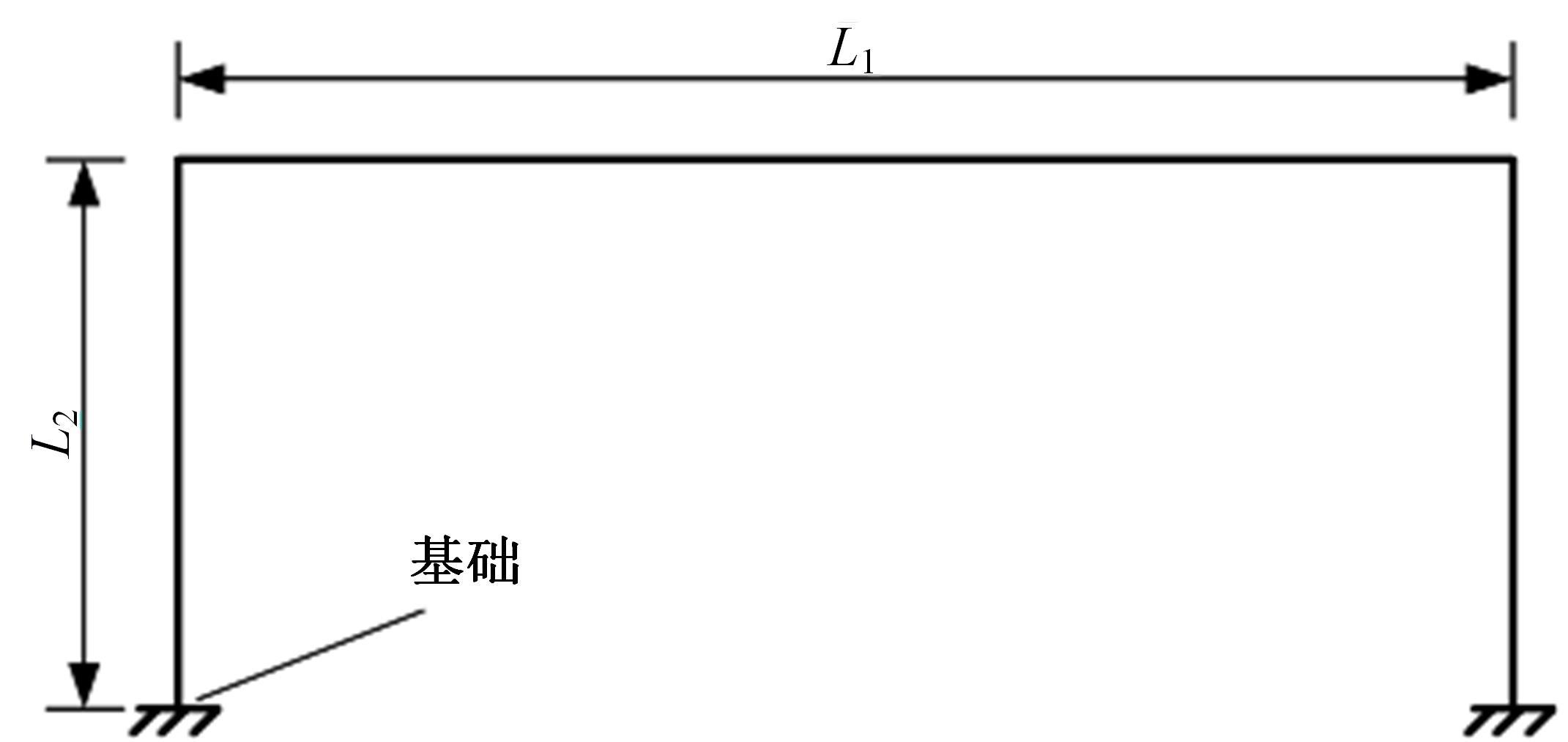
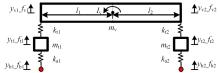
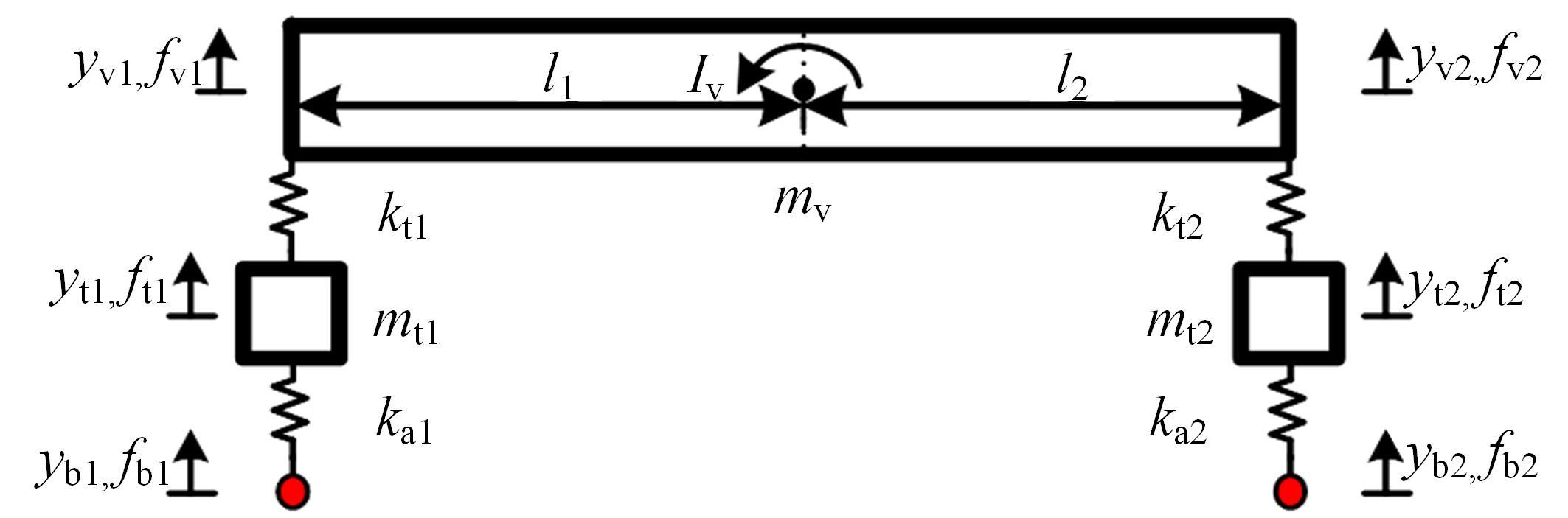
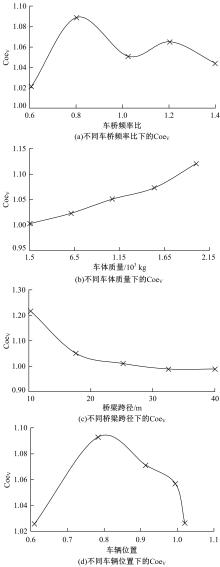
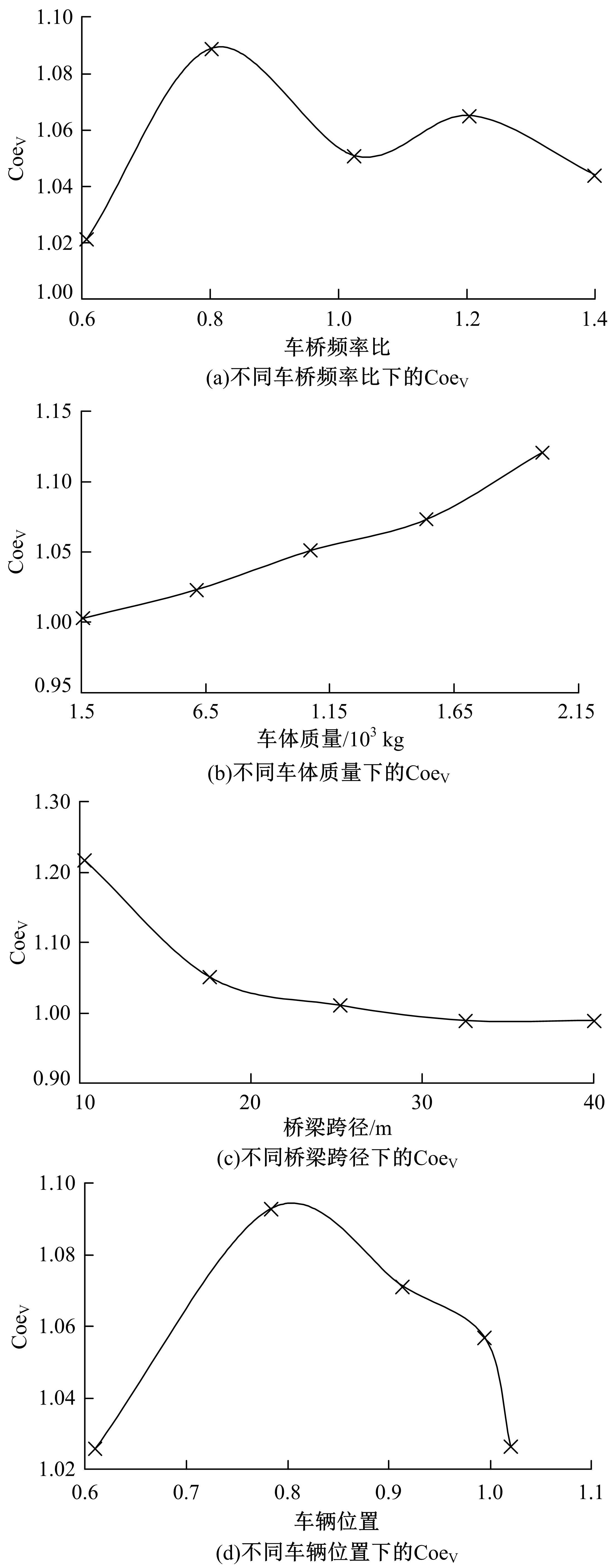
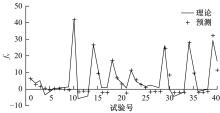
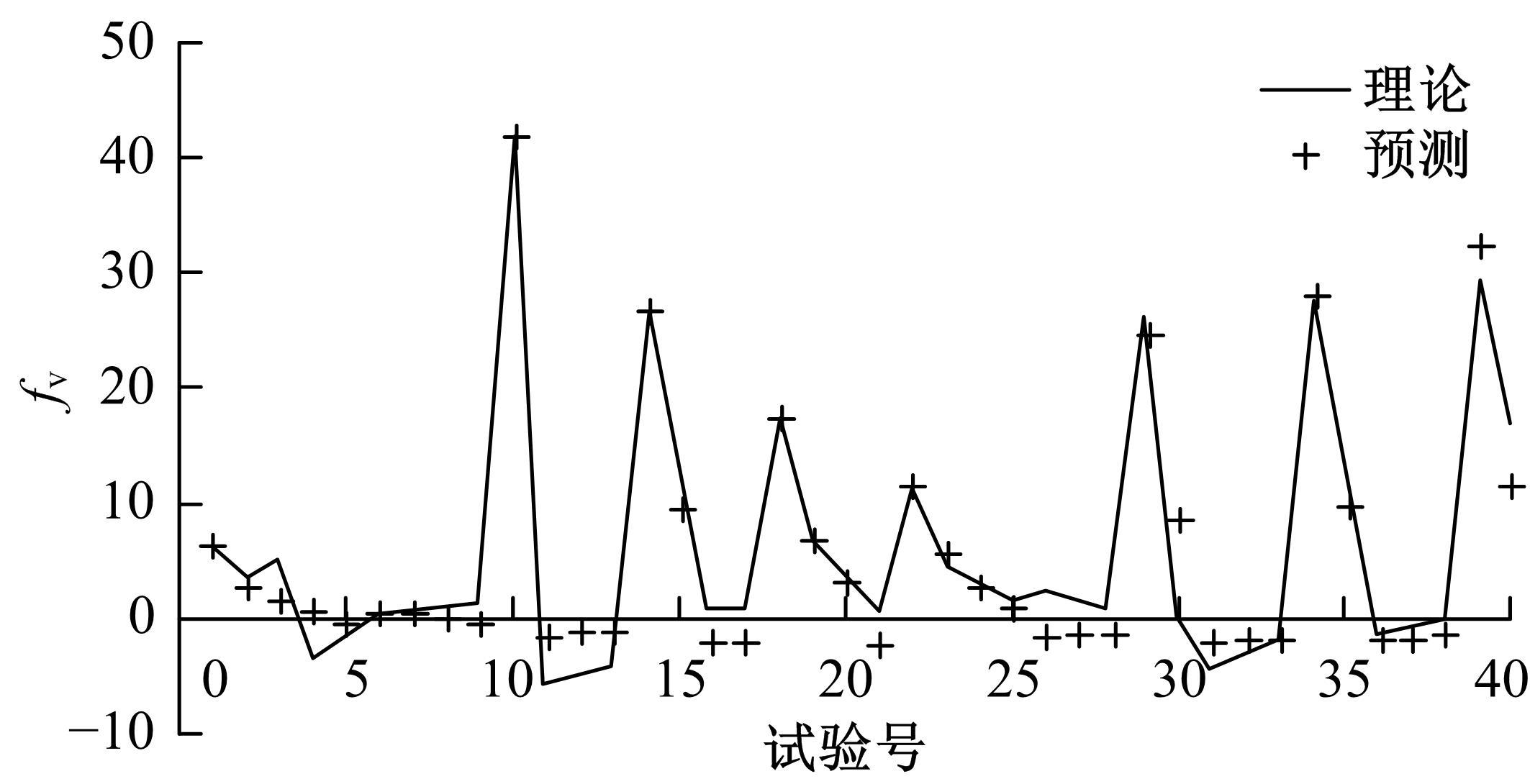
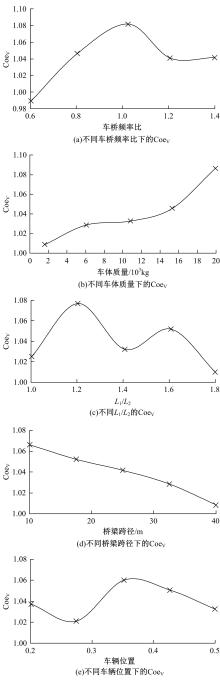
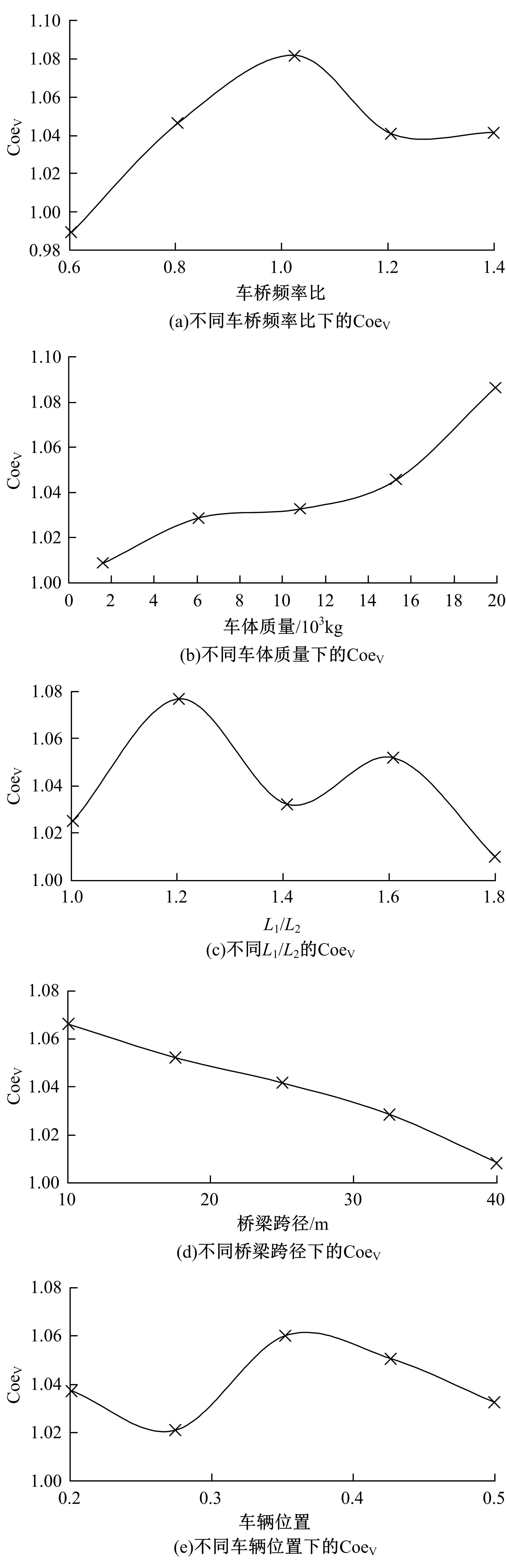
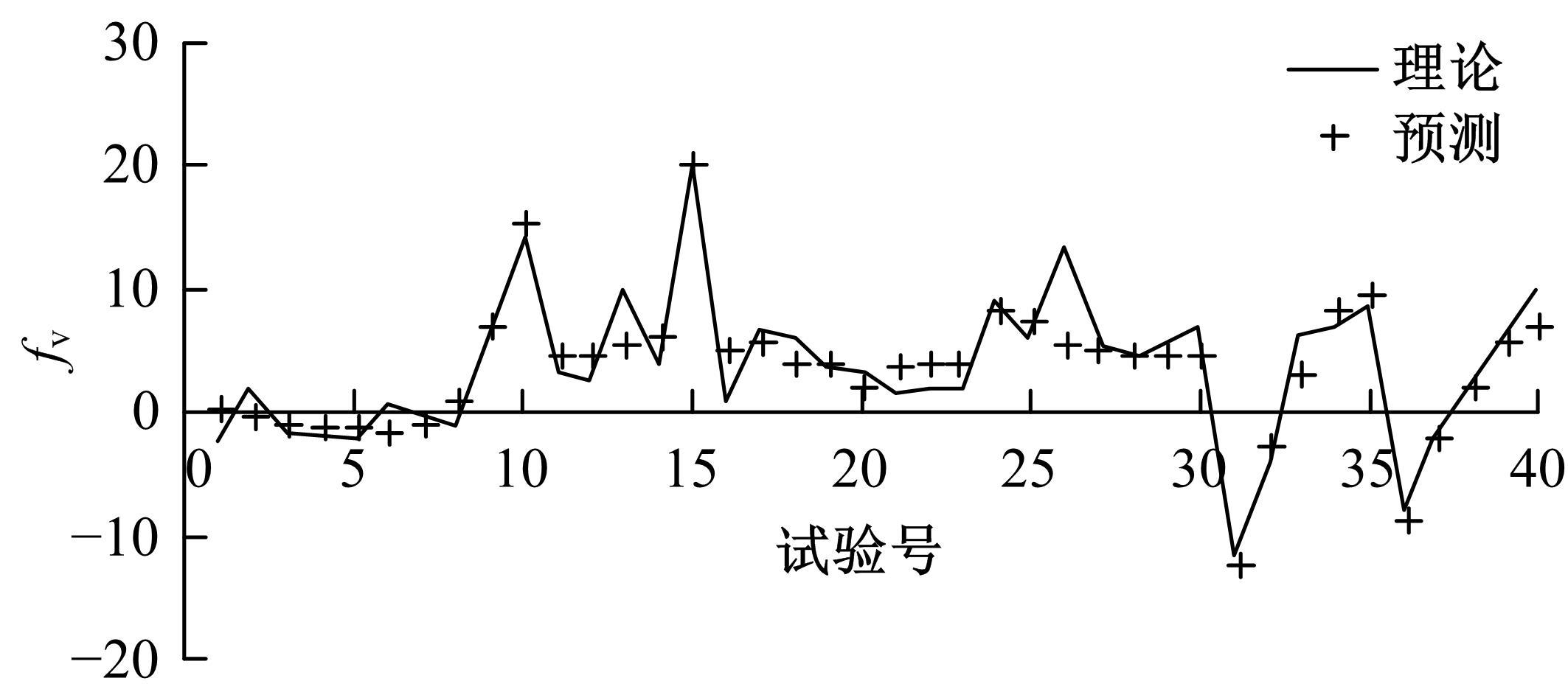
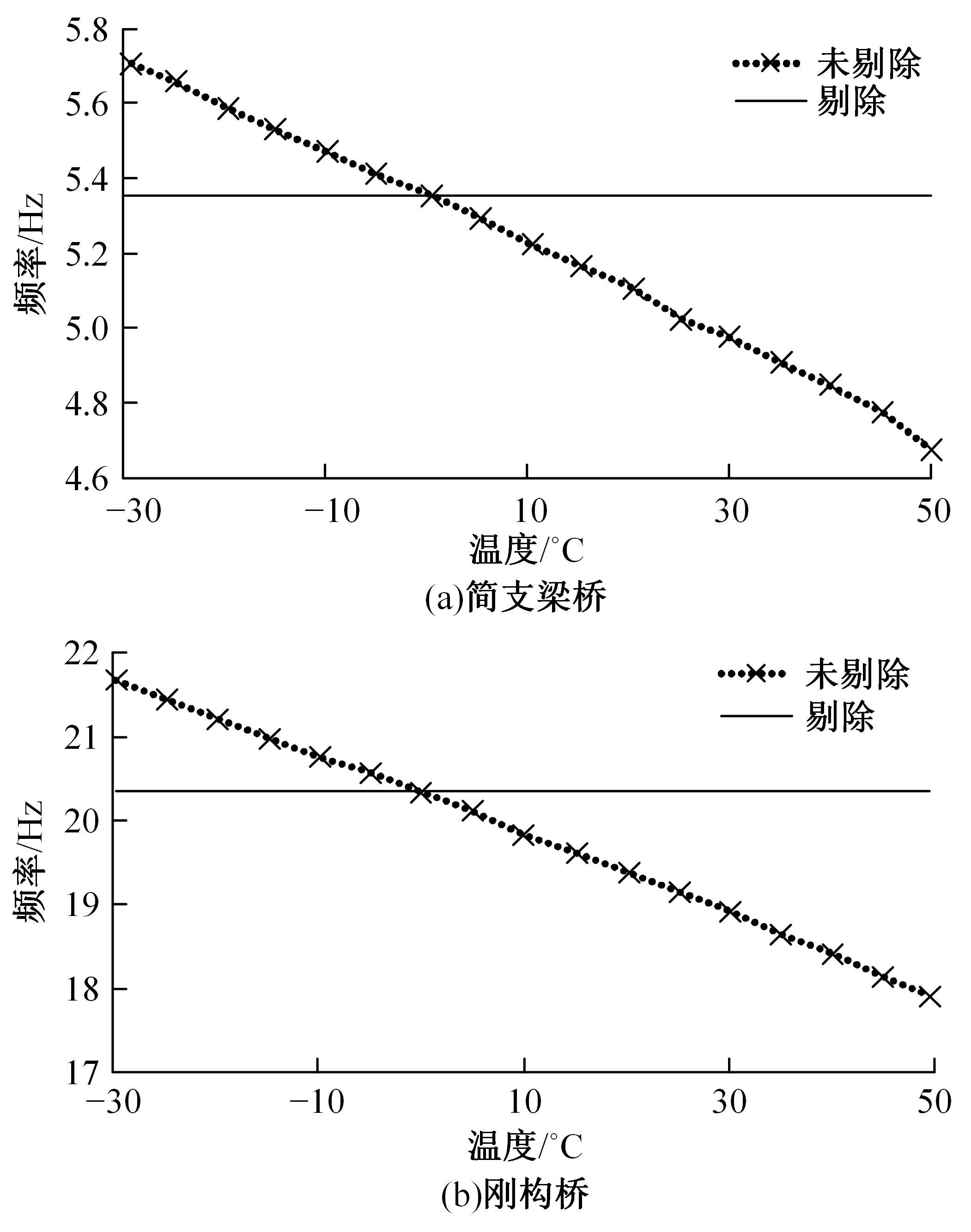
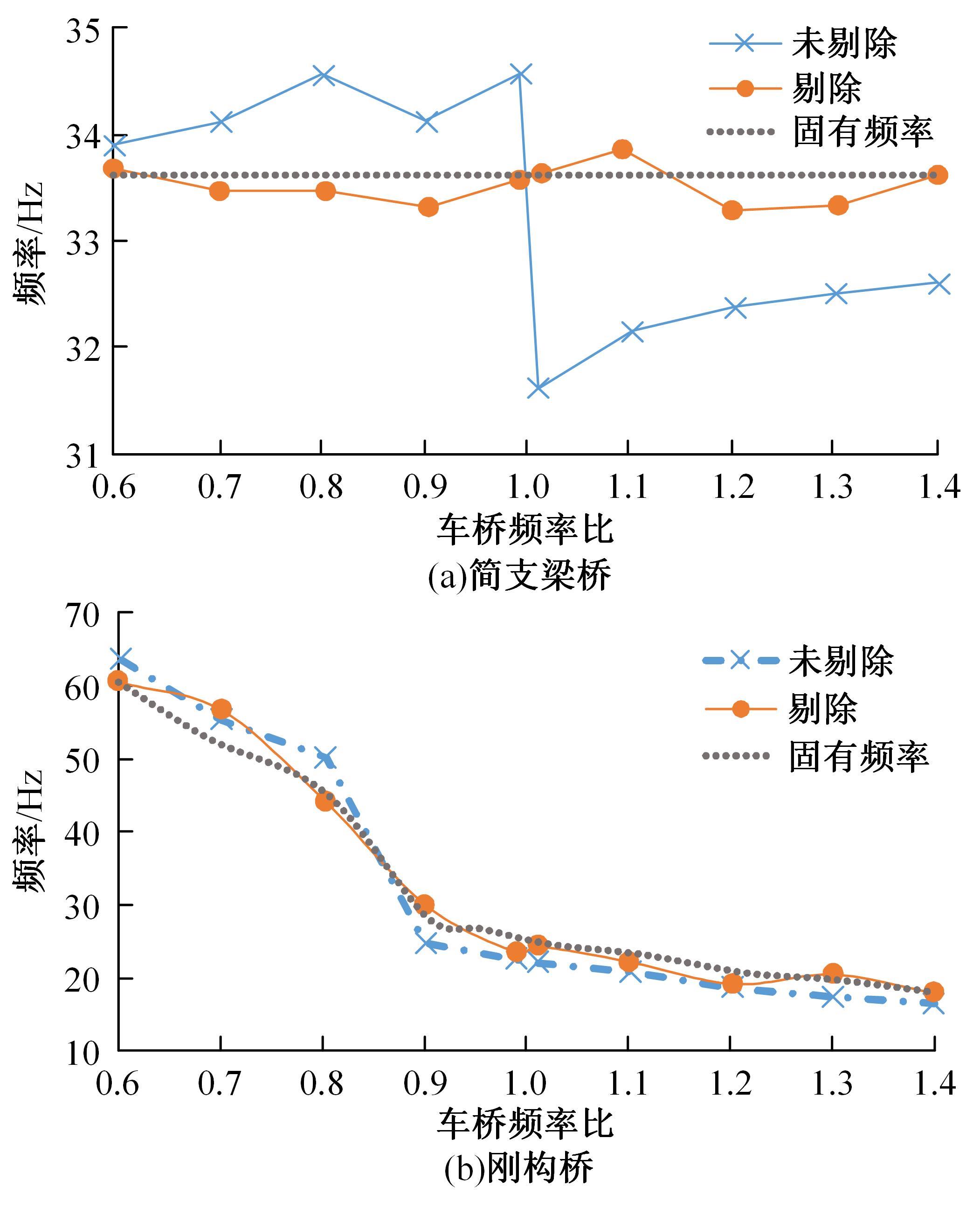
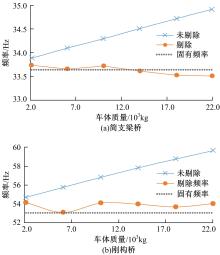
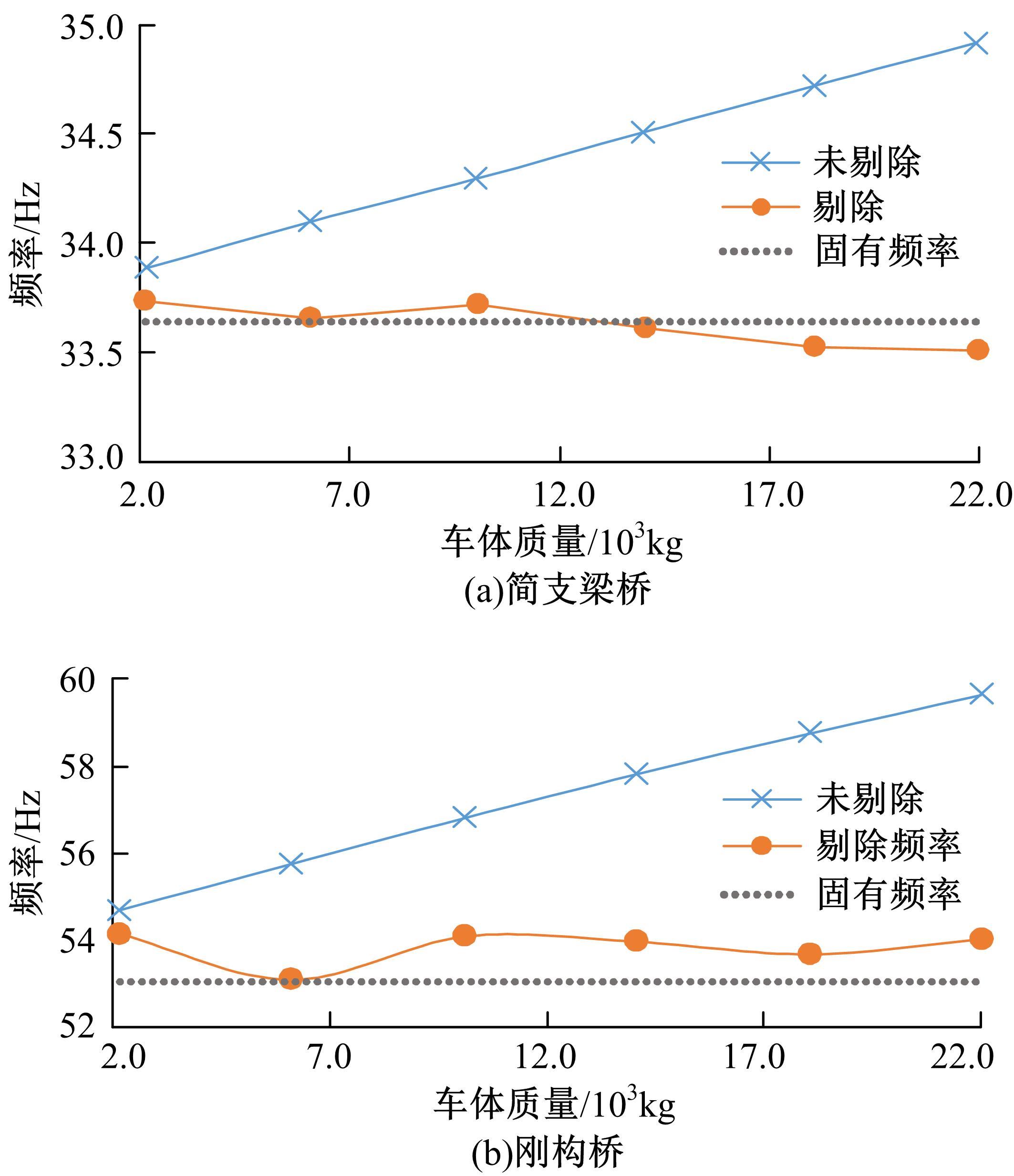
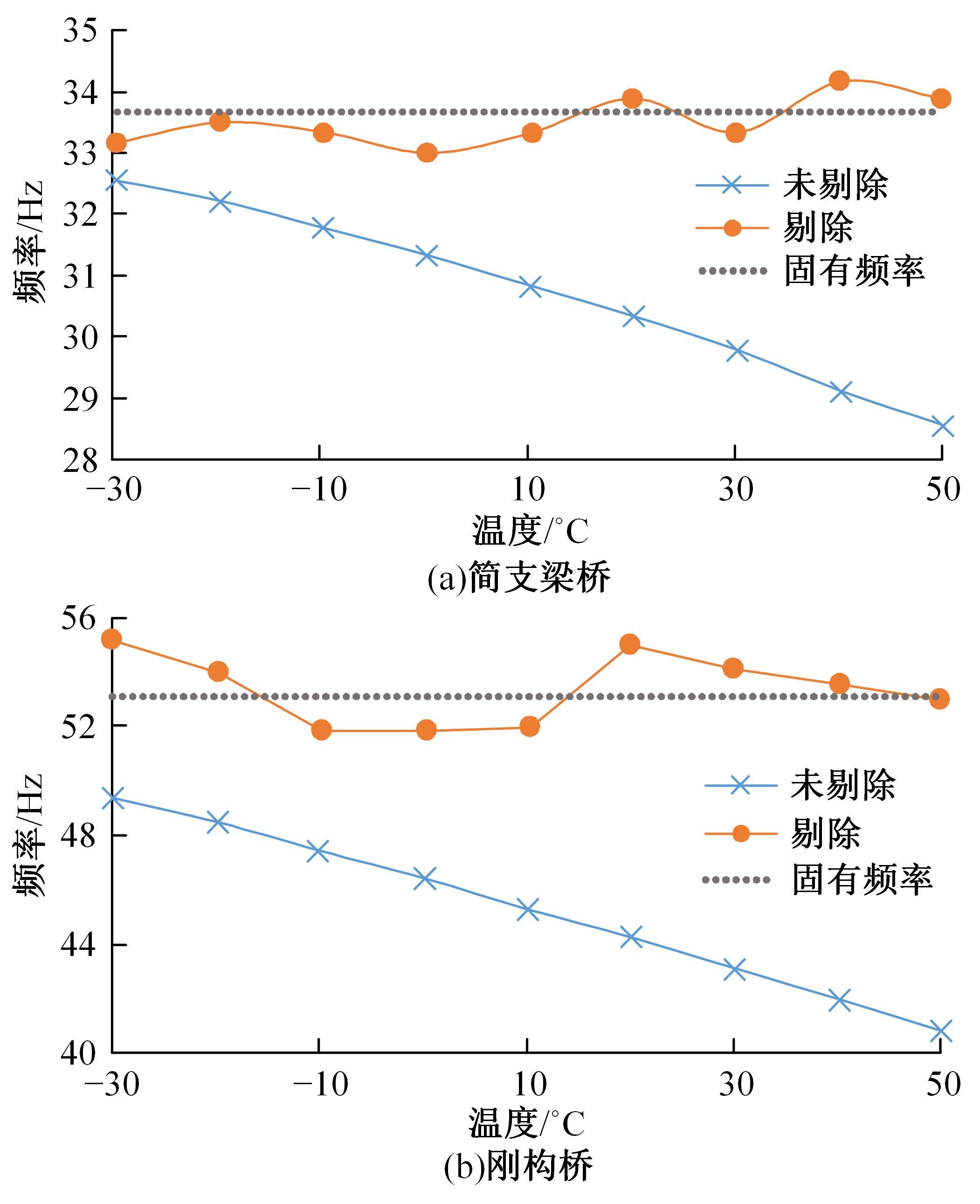
针对桥梁结构损伤识别和状态评估过程中测得的固有频率受到温度和车辆作用的显著影响，导致频率测试结果出现误差的问题，引入频率变异系数，基于温度理论分析模型和车辆参数规律对桥梁频率理论公式进行简化并提炼出关键影响因素，形成剔除温度与车辆作用的桥梁频率变异系数的经验公式。通过简支梁桥和门式刚构桥算例验证了剔除方法的准确性，结果表明，利用经验公式计算的频率与理论计算结果相差较小，能够很好地表征纯净的梁式桥频率，提高利用频率变化评估桥梁安全性的精确度。

关键词: 桥梁工程, 温度, 车辆作用, 因素剔除, 桥梁频率

Abstract:

Aiming at the problem that the natural frequency measured in the process of damage identification and state assessment of bridge structure is significantly affected by temperature and vehicle action， resulting in errors in frequency test results， the frequency coefficient of variation was introduced， the bridge frequency theory formula was simplified based on the temperature theory analysis model and the vehicle parameter law， and the key influencing factors were extracted to form an empirical formula for the bridge frequency coefficient of variation that excludes temperature and vehicle action. The results show that the bridge frequency calculation results obtained by the elimination method in this paper have little difference with the theoretical calculation results， which can well characterize the frequency of pure beam bridge and improve the accuracy of assessing the safety of bridge by using frequency variation.

Key words: bridge engineering, temperature, vehicle effect, factor elimination, bridge frequency

中图分类号:

U446

袁野. 温度和车辆作用下梁式桥梁结构固有频率分析方法[J]. 吉林大学学报(工学版), 2023, 53(6): 1702-1710.

Ye YUAN. Natural frequency analysis of beam bridge structure under temperature and vehicle action[J]. Journal of Jilin University(Engineering and Technology Edition), 2023, 53(6): 1702-1710.

图/表 15

图1

图2

表1

车辆参数列表"

含义	取值
前轮（后轮）轮胎刚度k_a1（k_a2）/（N·m^-1）	2.41 $×$ 10⁷
前轮（后轮）质量m_t1（m_t2）/kg	1500
前（后）悬架刚度k_t1（k_t2）/（N·m^-1）	2.5 $×$ 10⁷
车身质量中心距前端（后端）距离l₁（l₂ ）/m	2
车身转动惯量I_v/（kg·m²）	1.48 $×$ 10⁵
车身质量m_v/kg	1.78 $×$ 10⁴

表1

表2

图3

表3

图4

表4

图5

表5

图6

图7

图8

图9

图10

参考文献 18

1	Aktan A E, Catbas F N, Grimmelsman K A, et al. Issues in infrastructure health monitoring for management[J]. Journal of Engineering Mechanics, 2000, 126(7): 711-724.
2	李惠, 周文松, 欧进萍, 等. 大型桥梁结构智能健康监测系统集成技术研究[J]. 土木工程学报,2006,39(2): 46-52.
	Li Hui, Zhou Wen-song, Jin-ping Ou, et al. A study on system integration technique of intelligent monitoring system for soundness of long-span bridges[J]. China Civil Engineering Journal, 2006, 39(2): 46-52.
3	宗周红, 张坤, 廖聿宸, 等. 考虑运营环境不确定性的斜拉桥模态频率识别[J]. 中国公路学报, 2019, 32(11): 40-50.
	Zong Zhou-hong, Zhang Kun, Liao Yu-chen, et al. Modal frequency identification of cable-stayed bridges considering uncertainties of operational environmental factors[J]. China Journal of Highway and Transport, 2019, 32(11): 40-50.
4	Behmanesh I, Moaveni B. Probabilistic identification of simulated damage on the dowling hall footbridge through bayesian finite element model updating[J]. Structural Control and Health Monitoring, 2015, 22(3): 463-483.
5	Kim C Y, Jung D S, Kim N S, et al. Effect of vehicle weight on natural frequencies of bridges measured from traffic-induced vibration[J]. Earthquake Engineering and Engineering Vibration, 2003, 2(1): 109-115.
6	夏樟华, 林友勤, 张景杭, 等. 环境温度对连续箱梁刚构桥相对小波熵指标的影响研究[J]. 振动与冲击,2017,36(1): 207-214.
	Xia Zhang-hua, Lin You-qin, Zhang Jing-hang, et al. Study on the influence of ambient temperature on the relative wavelet entropy index of continuous box girder rigid frame bridges[J]. Vibration and impact, 2017, 36(1): 207-214.
7	邓杨, 李爱群, 刘扬. 桥梁模态频率异常变化的概率检测方法及例证[J]. 振动工程学报, 2015, 28(6): 887-895.
	Deng Yang, Li Ai-qun, Liu Yang. Probabilistic detection method and its illustration for abnormal change of bridge's modal frequencies[J]. Journal of Vibration Engineering, 2015, 28(6): 887-895.
8	Xu Z D, Wu Z. Simulation of the effect of temperature variation on damage detection in a long-span cable-stayed bridge[J]. Structural Health Monitoring, 2007, 6(3): 177-189.
9	Xia Y, Hao H, Zanardo G, et al. Long term vibration monitoring of an RC slab: temperature and humidity effect[J]. Engineering Structures, 2006, 28(3): 441-452.
10	Rücker W F, Said S, Rohrmann R G, et al. Load and condition monitoring of a highway bridge in a continuous manner[C]∥Proceedings of the IABSE Symposium on Extending the Lifespan of Structures, San Francisco, CA, USA, 1995: No.108128.
11	Roeck G D, Wahab M A. Effect of temperature on dynamic system parameters of a highway bridge[J]. Structural Engineering International, 1997, 7(4): 266-270.
12	谭国金, 宫亚峰, 程永春, 等. 基于有载频率的简支梁桥自振频率计算方法[J]. 振动工程学报, 2011, 24(1): 31-35.
	Tan Guo-jin, Gong Ya-feng, Cheng Yong-chun, et al. Calculation for natural frequency of simply supported beam bridges based on loaded frequency[J]. Journal of Vibration Engineering, 2011, 24(1): 31-35.
13	贺文宇, 丁绪聪, 任伟新. 环境激励下移动车辆对桥梁模态参数识别的影响研究[J]. 振动与冲击, 2021, 40(3): 48-53.
	He Wen-yu, Ding Xu-cong, Ren Wei-xin. Effects of moving vehicle on bridge modal parametric identification under ambient excitation[J]. Vibration and shock, 2021, 40(3): 48-53.
14	de Roeck G, Maeck J, Michielsen T, et al. Traffic-induced shifts in modal properties of bridges[C]∥Proceedings of SPIE-The International Society for Optical Engineering, 2002, California, USA, 4753: 630-636.
15	程永春, 谭国金, 刘寒冰, 等. 基于特征解统计特性的桥梁损伤识别[J]. 吉林大学学报: 工学版, 2008,37(4): 812-816.
	Cheng Yong-chun, Tan Guo-jin, Liu Han-bing, et al. Damage identification of bridge structure based on statistical properties of eigen-solution[J]. Journal of Jilin University (Engineering and Technology Edition), 2008, 37(4): 812-816.
16	王华. 温度和车辆耦合作用下梁式桥动力特性分析[D]. 长春:吉林大学交通学院, 2018.
	Wang Hua. Dynamic characteristics analysis of beam-like bridges under the coupling effect of temperature and vehicles[D]. Changchun: College of Transportation, Jilin University, 2018.
17	Liu H B, Wang X Q, Jiao Y B. Effect of temperature variation on modal frequency of reinforced concrete slab and beam in cold regions[J]. Shock and Vibration, 2016(6): 1-17.
18	王文盛. 车辆作用下具有裂缝的中小跨径梁式桥的自振特性分析[D]. 长春: 吉林大学交通学院, 2017.
	Wang Wen-sheng. Free vibration characteristics analysis of small and medium span cracked beam bridges considering bridge-vehicle interaction[D]. Changchun: College of Transportation, Jilin University, 2017.

相关文章 15

[1]	冯宇,郝键铭,王峰,张久鹏,黄晓明. 非平稳极端风作用下大跨桥梁瞬态风致效应分析[J]. 吉林大学学报(工学版), 2023, 53(6): 1638-1649.
[2]	王华,王龙林,张子墨,何昕. 基于裂缝宽度变化的连续刚构桥安全性预警技术[J]. 吉林大学学报(工学版), 2023, 53(6): 1650-1657.
[3]	王俊,李加武,王峰,张久鹏,黄晓明. 简化U形峡谷风速分布及其对悬索桥抖振响应的影响[J]. 吉林大学学报(工学版), 2023, 53(6): 1658-1668.
[4]	王峰,刘双瑞,王佳盈,宋佳玲,王俊,张久鹏,黄晓明. 尺寸和形状效应对多孔结构风阻系数的影响[J]. 吉林大学学报(工学版), 2023, 53(6): 1677-1685.
[5]	吴春利,黄诗茗,李魁,顾正伟,黄晓明,张炳涛,杨润超. 基于数值仿真和统计分析的洪水作用下桥墩作用效应分析[J]. 吉林大学学报(工学版), 2023, 53(6): 1612-1620.
[6]	谭国金,孔庆雯,何昕,张攀,杨润超,朝阳军,杨忠. 基于动力特性和改进粒子群优化算法的桥梁冲刷深度识别[J]. 吉林大学学报(工学版), 2023, 53(6): 1592-1600.
[7]	江辉,李新,白晓宇. 桥梁抗震结构体系发展述评：从延性到韧性[J]. 吉林大学学报(工学版), 2023, 53(6): 1550-1565.
[8]	刘子玉,陈士通,支墨墨,黄晓明,陈哲心. 可“临-永”转换抢修钢墩应急使用极限承载力[J]. 吉林大学学报(工学版), 2023, 53(6): 1601-1611.
[9]	张玥,刘传森,宋飞. 桥台背墙对连续梁桥地震易损性的影响[J]. 吉林大学学报(工学版), 2023, 53(5): 1372-1380.
[10]	兰树伟,周东华,陈旭,莫南明. 双柱式高墩桥梁整体稳定性的实用算法[J]. 吉林大学学报(工学版), 2023, 53(4): 1105-1111.
[11]	王登峰,陈宏利,那景新,陈鑫. 单双搭接接头经高温老化后的失效对比[J]. 吉林大学学报(工学版), 2023, 53(2): 346-354.
[12]	孙琪凯,张楠,刘潇,周子骥. 基于Timoshenko梁理论的钢-混组合梁动力折减系数[J]. 吉林大学学报(工学版), 2023, 53(2): 488-495.
[13]	刘聂玚子,荣鑫,刘洪海,边庆华,兰海. 沥青混合料的搅拌功率试验和黏度模型[J]. 吉林大学学报(工学版), 2023, 53(1): 220-225.
[14]	卢晓红,乔金辉,周宇,马冲,隋国川,孙卓. 搅拌摩擦焊温度场研究进展[J]. 吉林大学学报(工学版), 2023, 53(1): 1-17.
[15]	叶华文,段智超,刘吉林,周渝,韩冰. 正交异性钢⁃混组合桥面的轮载扩散效应[J]. 吉林大学学报(工学版), 2022, 52(8): 1808-1816.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

水平	因素
水平	1-车辆位置	2-跨径/m	3-车桥频率比	4-车体质量/kg
1	0.59	10.0	0.60	1500
2	0.76	17.5	0.80	6125
3	0.89	25.0	1.02	10 750
4	0.97	32.5	1.20	15 375
5	1.00	40.0	1.40	20 000

系数	拟合值	系数	拟合值
p₁	-12.65	p₉	10.45
p₂	19.30	p₁₀	-19.32
p₃	-3.96	p₁₁	30.77
p₄	2.14	p₁₂	-3.13
p₅	0.05	p₁₃	6.60
p₆	0.24	p₁₄	-15.91
p₇	0.000177	p₁₅	11.98
p₈	1.82	p₁₆	-2.53

水平	因素
水平	车桥频率比	车体质量/kg	L₁/L₂	跨径/m	车辆位置
1	0.6	1 500	1	10	0.2
2	0.8	6 125	1.2	17.5	0.275
3	1.02	10 750	1.4	25	0.35
4	1.2	15 375	1.6	32.5	0.425
5	1.4	20 000	1.8	40	0.5

系数	拟合值	系数	拟合值
q₁	14.76	q₁₁	0.36
q₂	-10.65	q₁₂	-1.91
q₃	0.75	q₁₃	-12.20
q₄	-1186	q₁₄	155.31
q₅	0.00	q₁₅	-232.10
q₆	-1832	q₁₆	-0.29
q₇	-0.45	q₁₇	27.21
q₈	-0.08	q₁₈	-67.19
q₉	-0.15	q₁₉	40.87
q₁₀	0.19	q₂₀	5.22