栓钉剪力连接件力学性能分析

doi:10.13229/j.cnki.jdxbgxb20210739

摘要/Abstract

摘要：

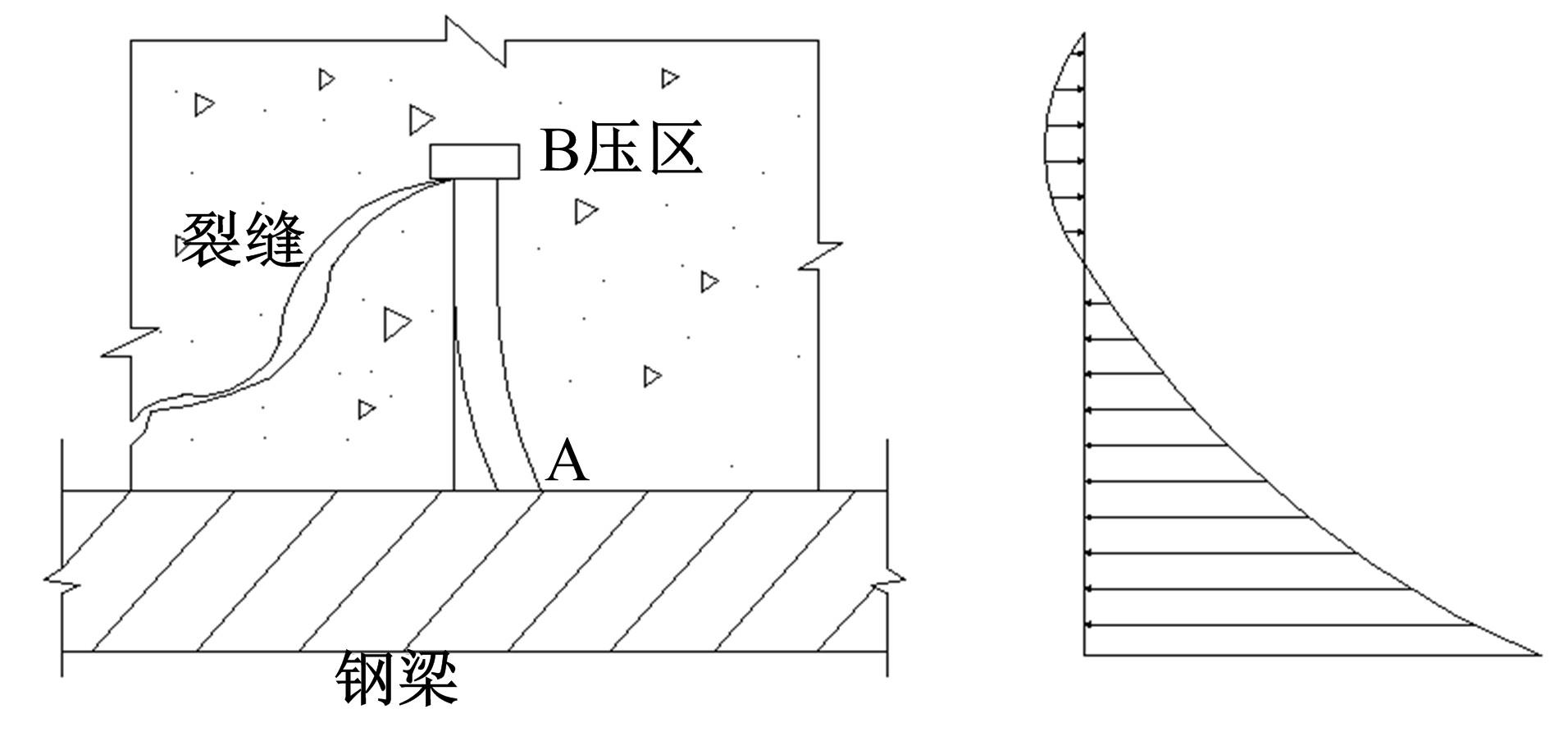
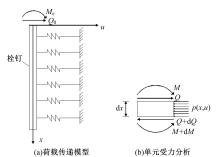
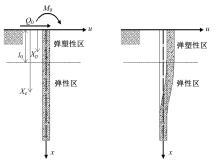
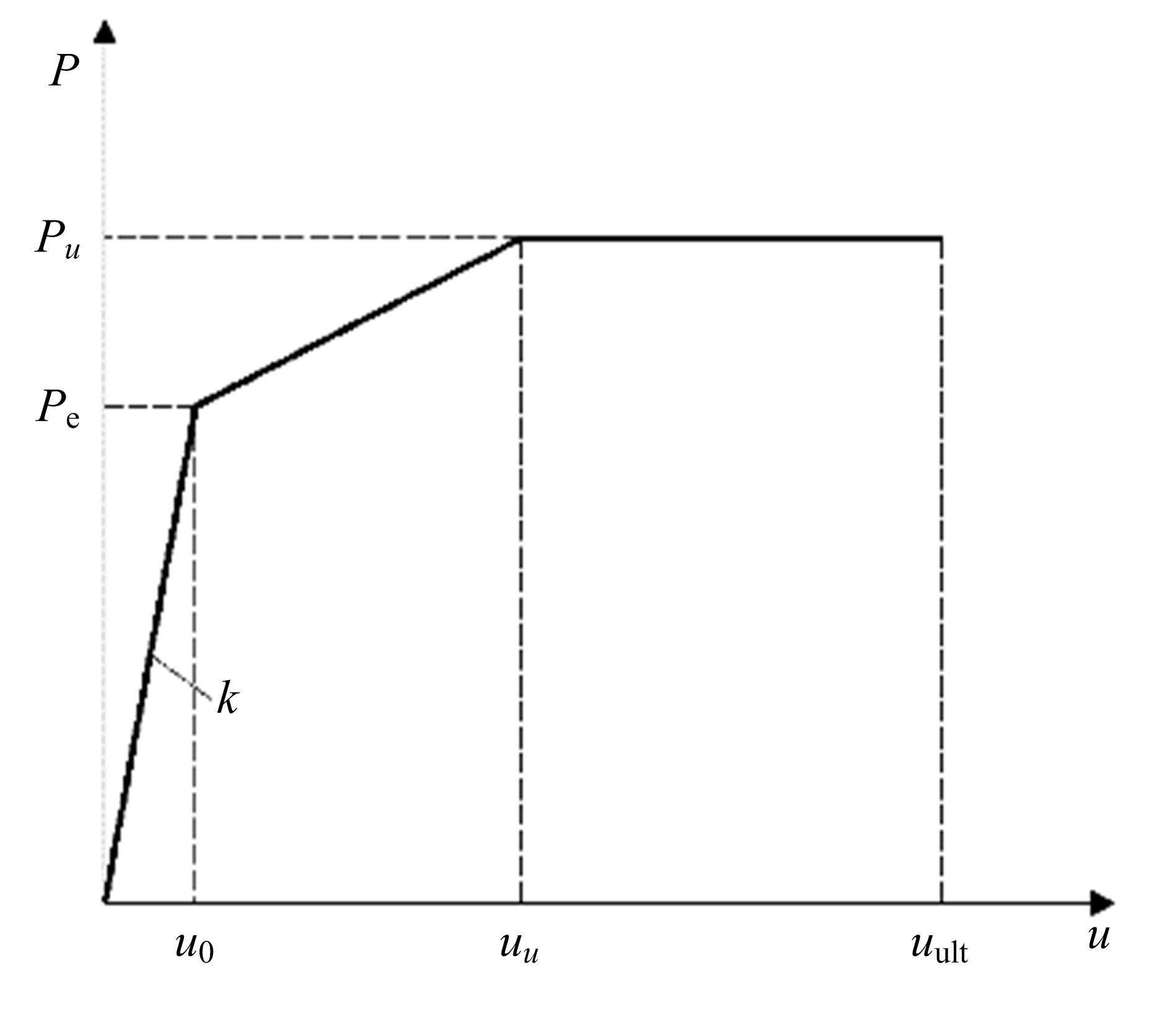
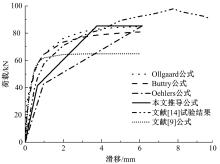
从栓钉剪力连接件受力机理与破坏模式分析出发，基于弹塑性地基中横向荷载作用下的单桩理论，建立栓钉剪力连接件的挠曲线微分方程。根据栓钉剪力连接件各阶段的受力特点，引入边界条件，对栓钉剪力连接件的挠曲线微分进行了求解分析，提出了栓钉剪力连接件的抗剪承载力、剪切刚度、弹性阶段末端的滑移值等的计算公式，建立了栓钉剪力连接件荷载-滑移的三折线本构模型，该模型具有数学形式简单且物理意义明确等特点。算例分析表明：栓钉剪力连接件抗剪承载力值、剪切刚度值、弹性末端滑移值、极限滑移值计算值分别为85.44 kN，64.92 kN/mm、0.64 mm、6.13 mm，计算值与试验值吻合较好；栓钉剪力连接件的三折线荷载-滑移关系曲线与Buttry与Ollgaard拟合的全曲线式荷载-滑移曲线较接近，且与栓钉剪力连接件的试验荷载滑移曲线吻合较好。

关键词: 结构工程, 钢-混凝土组合梁, 栓钉剪力连接件, 弹性地基梁, 抗剪承载力, 抗剪刚度

Abstract:

Based on the analysis of the stress mechanism and failure mode of stud shear connectors， the differential equation of the deflection line of stud shear connectors is established based on the theory of single pile under lateral load in elastoplastic foundation. According to mechanical characteristics in different stages of the stud shear connectors， the boundary conditions are introduced， the stud shear connectors of flexural differential is analyzed， and the calculation formulas of the shear bearing capacity， shear stiffness and elastic stage at the end of the slip value of the stud shear connectorscalculation formula are put forward. The load-slip tri-fold constitutive model of stud shear connectors is established, which has the characteristics of simple mathematical form and clear physical meaning. The results show that the calculated values of shear capacity， shear stiffness， elastic end slip and ultimate slip of stud shear connectors are 85.44 kN， 64.92 kN/mm， 0.64 mm and 6.13 mm respectively and the calculated values are in good agreement with the experimental values. The three-fold line load-slip relationship curve of stud shear connectors is close to the full-curve load-slip curve fitted by Buttry and Ollgaard， and it is in good agreement with the test load-slip curve of stud shear connectors.

Key words: structural engineering, steel-concrete composite beam, stud shear connector, elastic foundation beam, shear bearing capacity, the shear stiffness

中图分类号:

TU398.9

匡亚川,陈立斌,李超举,贺宇豪. 栓钉剪力连接件力学性能分析[J]. 吉林大学学报(工学版), 2023, 53(2): 538-546.

Ya-chuan KUANG,Li-bin CHEN,Chao-ju LI,Yu-hao HE. Analysis of mechanical properties of stud shear connectors[J]. Journal of Jilin University(Engineering and Technology Edition), 2023, 53(2): 538-546.

图/表 10

图1

图2

图3

图4

图5

表1

表2

表3

表4

图6

参考文献 19

1	聂建国. 钢-混凝土组合结构桥梁[M]. 北京: 人民交通出版社, 2011.
2	Oehlers D J, Johnson R P.The strength of stud shear connections in composite beams[J]. Structure Engineering, 1987, 65(2): 44-48.
3	Xue W C, Ding M, Wang H, et al. Static behavior and theoretical model of stud shear connectors[J]. Journal of Bridge Engineering, 2008, 13(6): 623-634.
4	Xi Qina, Yang G T. Elastic stiffness of stud connection in composite structures[J]. Steel and Composite Structures, 2021, 39(4): 419-433.
5	. European 4: design of composite steel and concrete structures part 2, general rules and rules for bridges [S].
6	陈俊, 汪威, 丁发兴, 等. 钢-混凝土组合梁高强螺栓抗剪连接件受剪性能[J].铁道科学与工程学报, 2019, 16(10): 2553-2561.
	Chen Jun, Wang Wei, Ding Fa-xing, et al. Shear behavior of high-strength bolt shear connectors of steel-concrete composite beams[J]. Journal of Railway Science and Engineering, 2019, 16(10): 2553-2561.
7	汪劲丰, 张爱平, 王文浩. 栓钉高度对栓钉连接件抗剪性能的影响[J]. 浙江大学学报: 工学版, 2020 54(11): 2076-2084.
	Wang Jin-feng, Zhang Ai-ping, Wang Wen-hao. Influence of tailor heighty on sears performance of tailor connectors[J]. Journal of Zhejiang University(Engineering Science), 2020 54(11): 2076-2084.
8	Shim C S, Lee P G, Yoon T Y. Static behavior of large stud shear connectors[J]. Engineering Structures the Journal of Earthquake Wind & Ocean Engineering, 2004, 26(12): 1853-1860.
9	丁发兴, 倪鸣. 栓钉剪力连接件滑移性能试验研究及受剪承载力计算[J]. 建筑工程学报, 2014, 35(9): 98-106.
	Ding Fa-xing, Ni Ming. Experimental study on slip performance of bolt screw shear connectors and calculation of shear bearing capacity[J]. Journal of Building Engineering, 2014, 35(9): 98-106.
10	王连广. 钢与混凝土组合结构理论与计算[M]. 北京: 科学出版社, 2005.
11	周景星. 基础工程[M]. 北京: 清华大学出版社, 2007.
12	张磊. 水平荷载作用下单桩性状研究[D]. 杭州: 浙江大学建筑工程学院, 2011.
	Zhang Lei. Research on single pile behavior under horizontal load[D]. Hangzhou: School of Architecture and Engineering, Zhejiang University, 2011.
13	Hsiung Y M. Theoretical elastic-plastic solution for laterally loaded piles[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2003, 129(5): 475-480.
14	聂建国, 谭英, 王洪全. 钢-高强混凝土组合梁栓钉剪力连接件的设计计算[J]. 清华大学学报: 自然科学版, 1999(12): 94-97.
	Nie Jian-guo, Tan Ying, Wang Hong-quan. Design and calculation of stud shear connectors for steel-high strength concrete composite beams[J]. Journal of Tsinghua University(Natural Science Edition), 1999(12): 94-97.
15	石卫华. 考虑耐久性的钢-混凝土组合梁结构力学性能研究及可靠性分析[D]. 长沙: 中南大学土木工程学院, 2013.
	Shi Wei-hua. Study on mechanical properties and reliability analysis of steel-concrete composite beam structures considering durability[D]. Changsha: School of Civil Engineering, Central South University, 2013.
16	Ollgaard J G, Slutter R G, Fisher J W. Shear strength of stud connectors in light weight and normal weight concrete[J]. AISC Engineering Journal, 1971, 71-10: 55-64.
17	. 钢结构设计标准 [S].
18	EN 1994—1-1. Eurcode 4: design of composite steel and concrete structures-Part 1-1: general rules and rules for buildings [S].
19	Qi J, Hu Y, Wang J, et al. Behavior and strength of headed stud shear connectors in ultra-high performance concrete of composite bridges[J]. Frontiers of Structural and Civil Engineering, 2019, 13(5): 1138-1149.

相关文章 15

[1]	王晓东,李宁静,李强. 高压脉冲放电破碎混凝土梁试验[J]. 吉林大学学报(工学版), 2023, 53(2): 496-504.
[2]	褚云朋,孙鑫晖,李明,姚勇,黄汉杰. 下击暴流作用下圆形马鞍面屋盖风压特性[J]. 吉林大学学报(工学版), 2022, 52(8): 1826-1833.
[3]	姚勇,苏留锋,李明,褚云朋,黄汉杰. 下击暴流作用下双面球壳型屋面风载特性[J]. 吉林大学学报(工学版), 2022, 52(3): 615-625.
[4]	匡亚川,宋哲轩,刘胤虎,莫小飞,伏亮明,罗时权. 新型装配式双舱综合管廊力学性能试验[J]. 吉林大学学报(工学版), 2022, 52(3): 596-603.
[5]	王毅红,田桥罗,兰官奇,姚圣法,张建雄,刘喜. 630 MPa高强钢筋混凝土大偏压柱受力性能试验[J]. 吉林大学学报(工学版), 2022, 52(11): 2626-2635.
[6]	龚永智,况锦华,柯福隆,周泉,罗小勇. UHPC连接的装配式剪力墙节点抗震性能试验[J]. 吉林大学学报(工学版), 2022, 52(10): 2367-2375.
[7]	樊学平,杨光红,尚志鹏,赵小雄,肖青凯,刘月飞. 考虑适用性的大跨桥梁主梁动态可靠性融合预测[J]. 吉林大学学报(工学版), 2022, 52(1): 144-153.
[8]	刘福寿,魏琦,徐文婷,谭国金. 基于弹性波传播和谱单元法的桁架结构损伤检测[J]. 吉林大学学报(工学版), 2021, 51(6): 2087-2095.
[9]	樊学平,杨光红,肖青凯,刘月飞. 大跨桥梁主梁失效概率分析的最优R-Vine Copula[J]. 吉林大学学报(工学版), 2021, 51(4): 1296-1305.
[10]	戴岩,聂少锋,周天华. 环梁式圆钢管约束H型钢混凝土柱-钢梁节点抗剪承载力[J]. 吉林大学学报(工学版), 2021, 51(3): 977-988.
[11]	于江,赵志浩,秦拥军. 基于声发射和分形的钢筋混凝土受剪梁损伤[J]. 吉林大学学报(工学版), 2021, 51(2): 620-630.
[12]	熊二刚,徐涵,谭赐,王婧,丁若愚. 基于弹塑性应力场理论的钢筋混凝土梁受剪承载力[J]. 吉林大学学报(工学版), 2021, 51(1): 259-267.
[13]	樊学平,屈广,刘月飞. 应用新数据同化算法的桥梁极值应力预测[J]. 吉林大学学报(工学版), 2020, 50(2): 572-580.
[14]	杨德磊,童乐为. 支管受轴向受拉工况下CHS-CFSHS T型节点应力集中系数计算公式[J]. 吉林大学学报(工学版), 2019, 49(6): 1891-1899.
[15]	戴岩, 聂少锋, 周天华. 带环梁的方钢管约束钢骨混凝土柱-钢梁节点滞回性能有限元分析[J]. 吉林大学学报(工学版), 2018, 48(5): 1426-1435.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

项目	抗剪承载力/kN	误差值/%
本文计算值	85.44	12.91
《钢结构设计标准》计算值	56.30	42.62
文献［9］计算值	65.77	32.96
文献［2］计算值	80.43	17.94
欧洲规范Eurocode4计算值	51.47	47.53
文献［15］试验值	98.10	-

项目	抗剪刚度/（kN·mm^-1）	误差值/%
本文计算值	64.92	21.25
《钢结构设计标准》计算值	56.30	31.71
欧洲规范Eurocode4计算值	64.79	21.41
Oehlers公式计算值	62.36	24.36
文献［15］试验值	82.44	-

项目	弹性末端滑移值/mm	误差值/%
本文计算值	0.64	6.66
Oehlers公式计算值	0.96	60
文献［15］试验值	0.60	-

项目	极限滑移值/mm	误差值/%
本文计算值	6.13	36.03
文献［9］计算值	6.25	34.83
文献［15］试验值	9.59	-