基于浮动坐标法的刚柔耦合定位平台力学模型

doi:10.13229/j.cnki.jdxbgxb.20220323

摘要/Abstract

摘要：

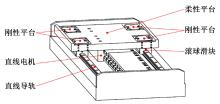
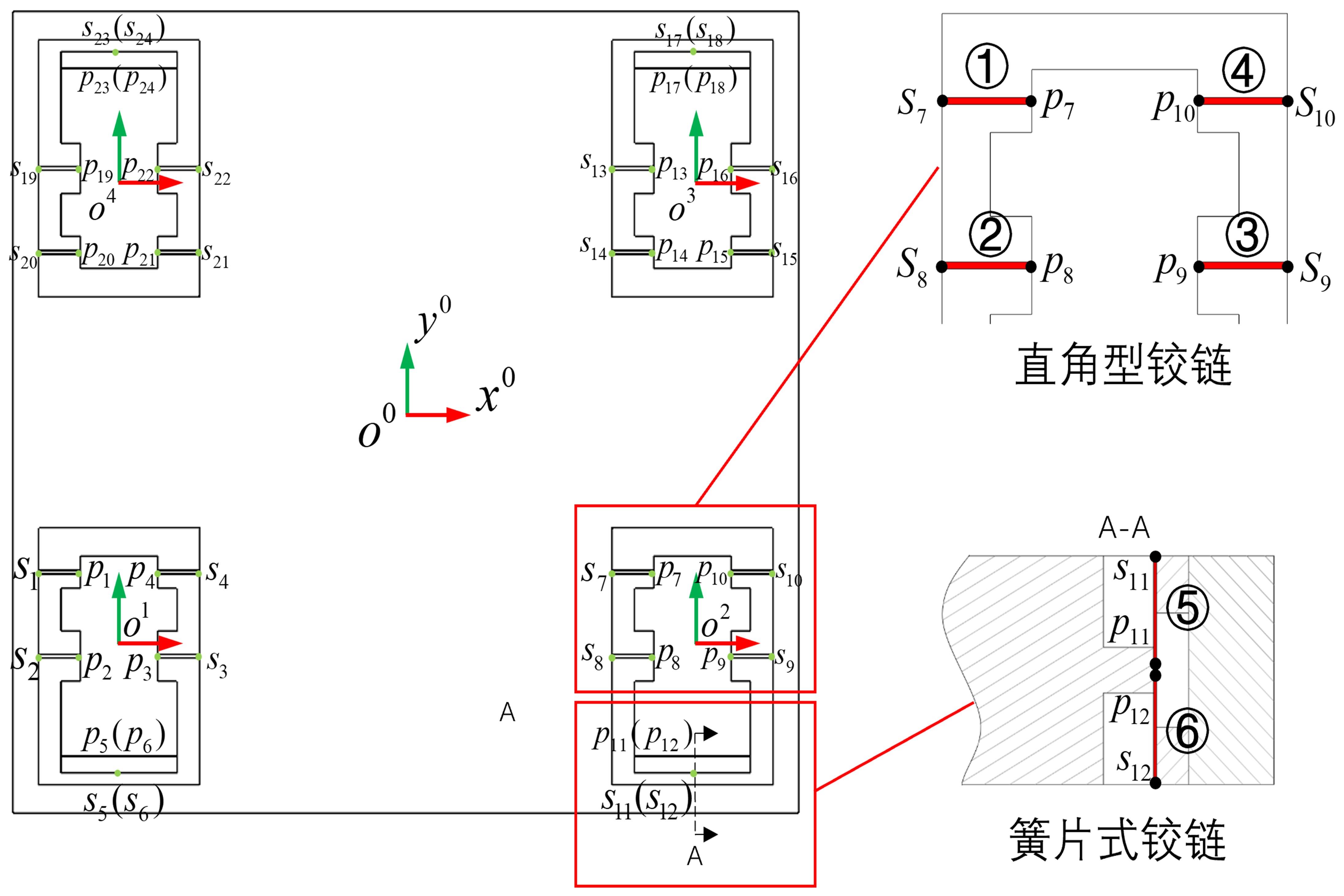
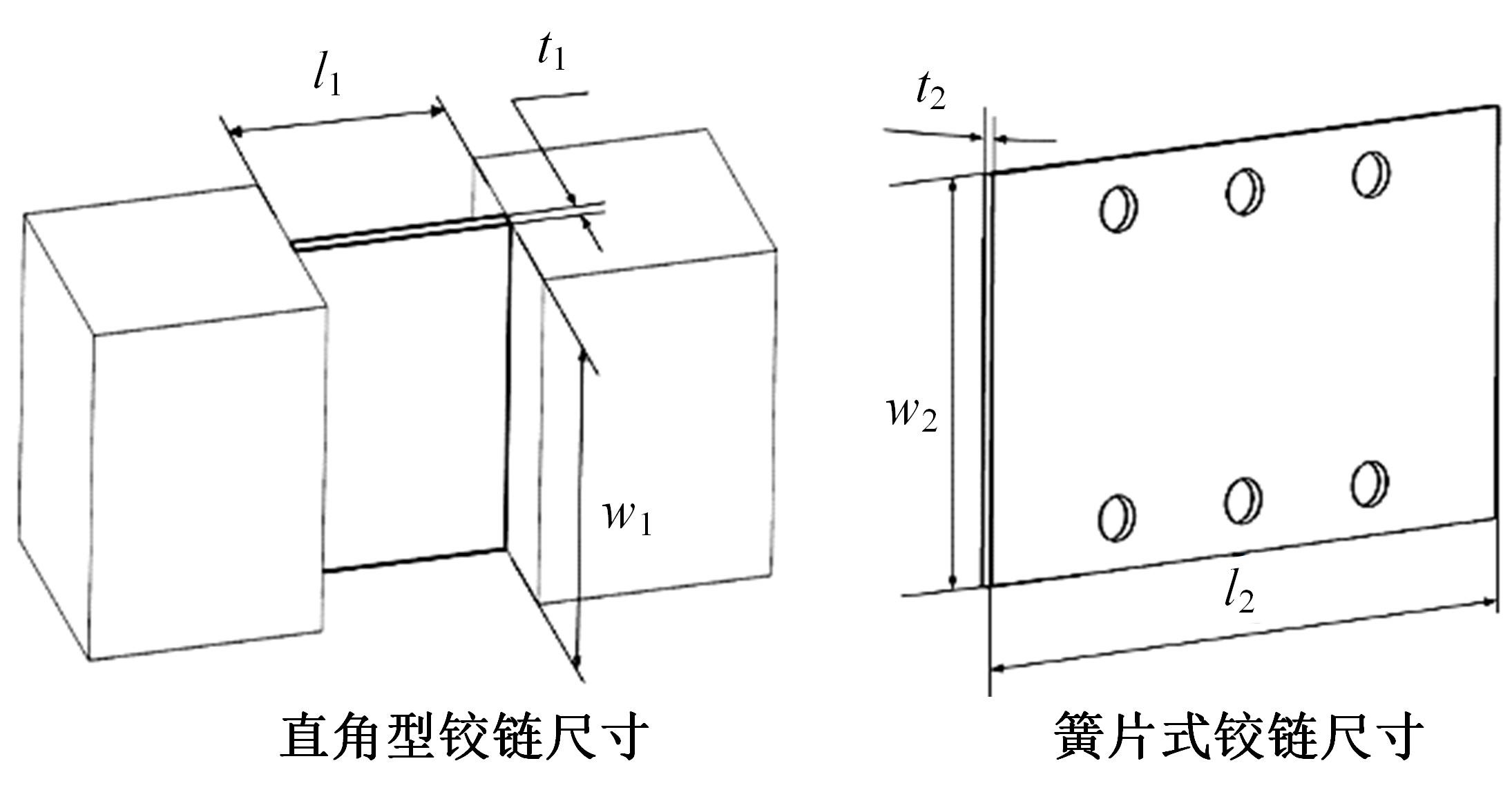
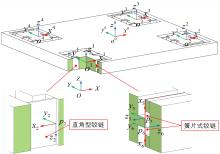
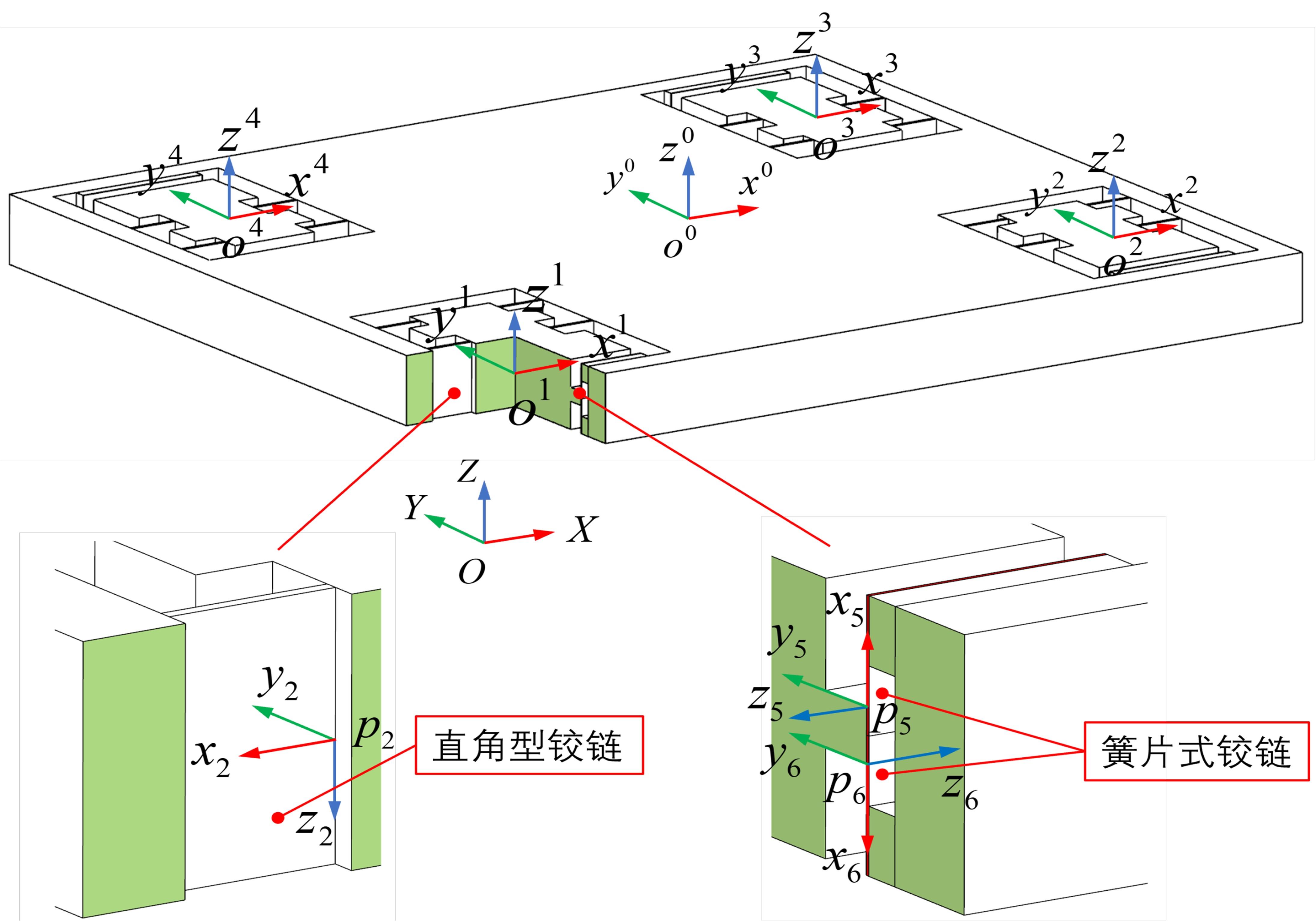
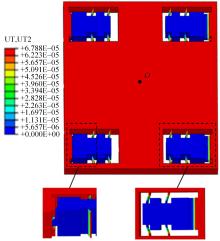
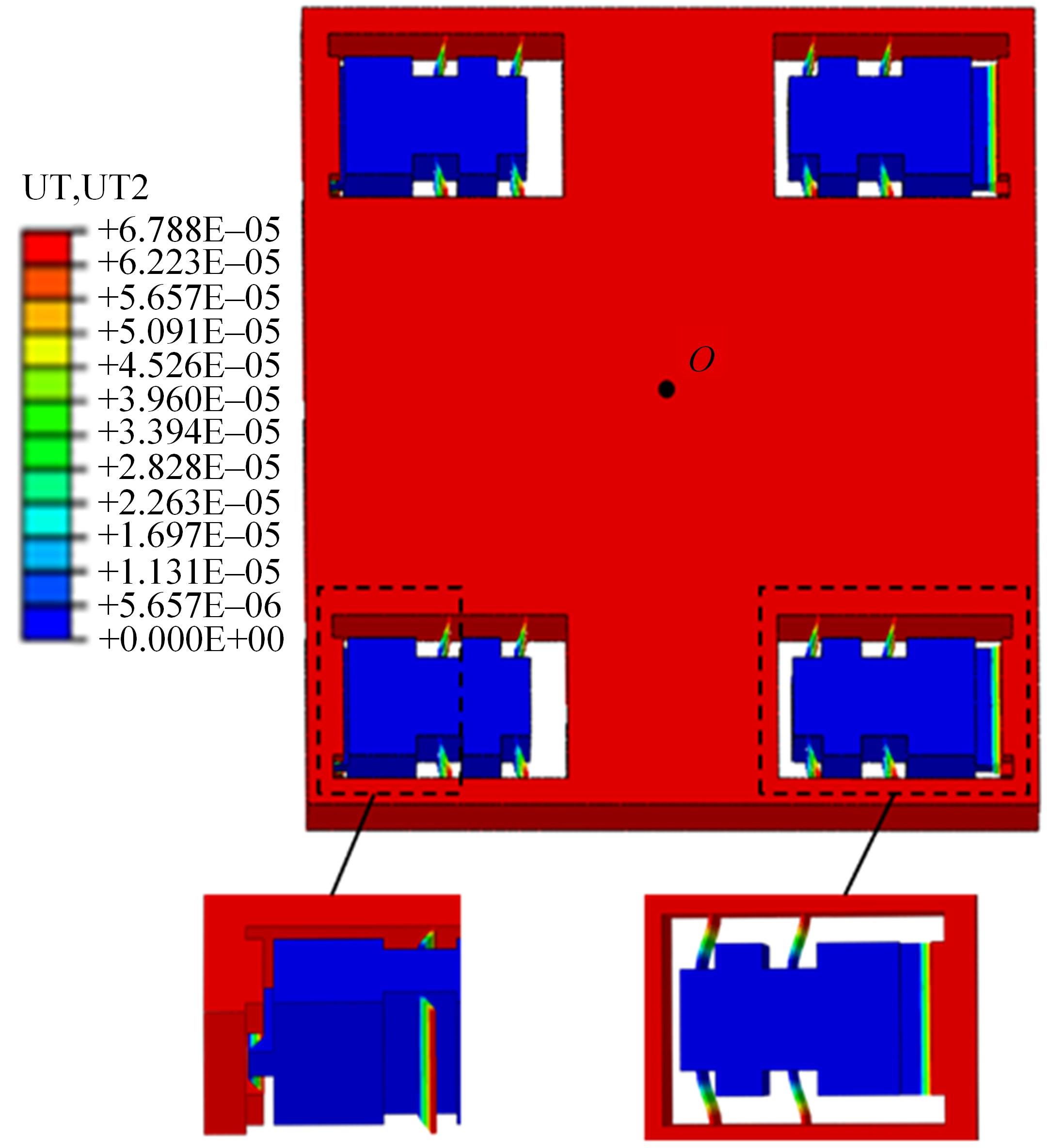
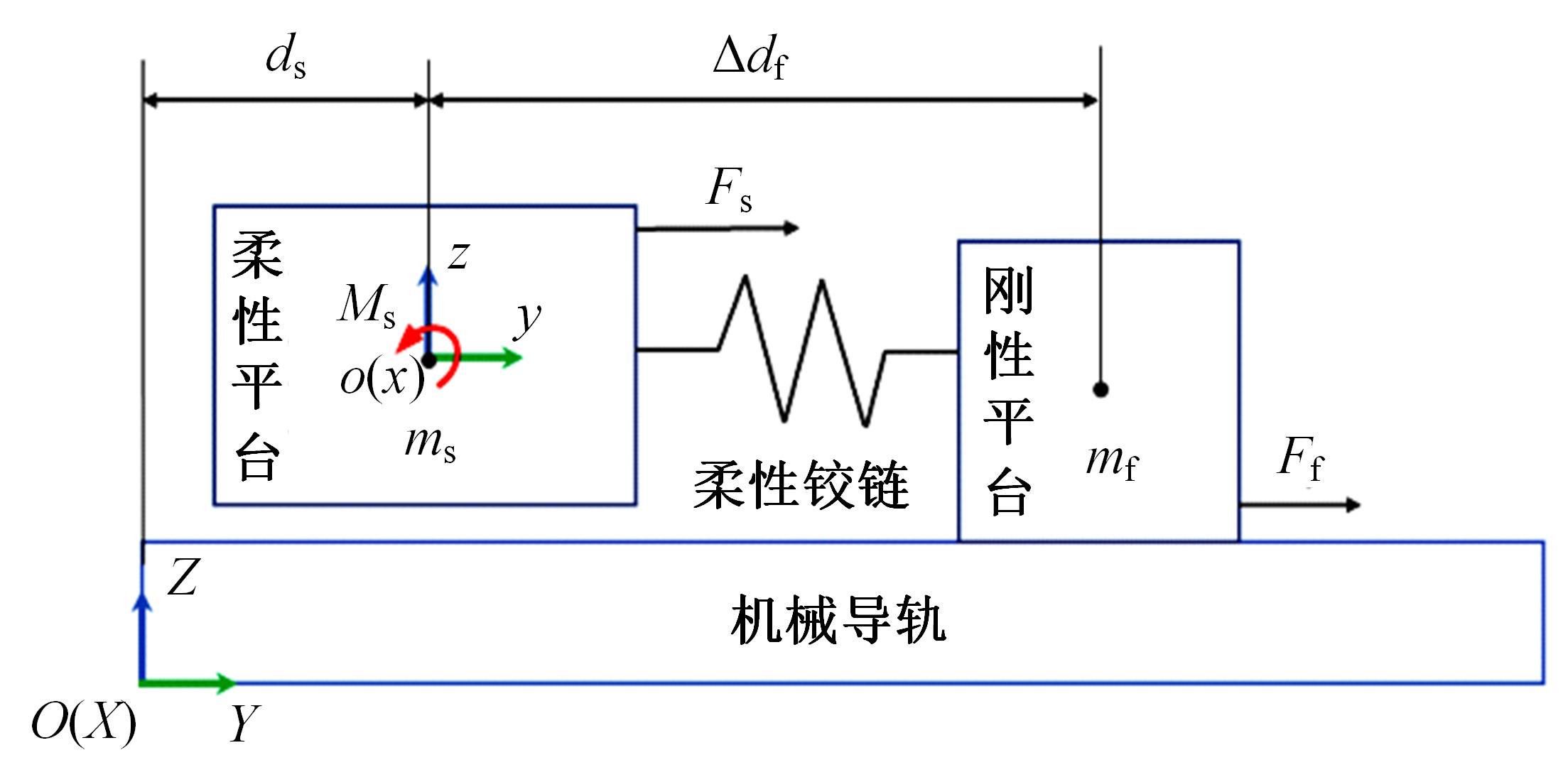
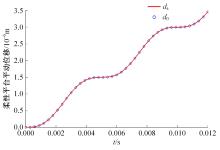
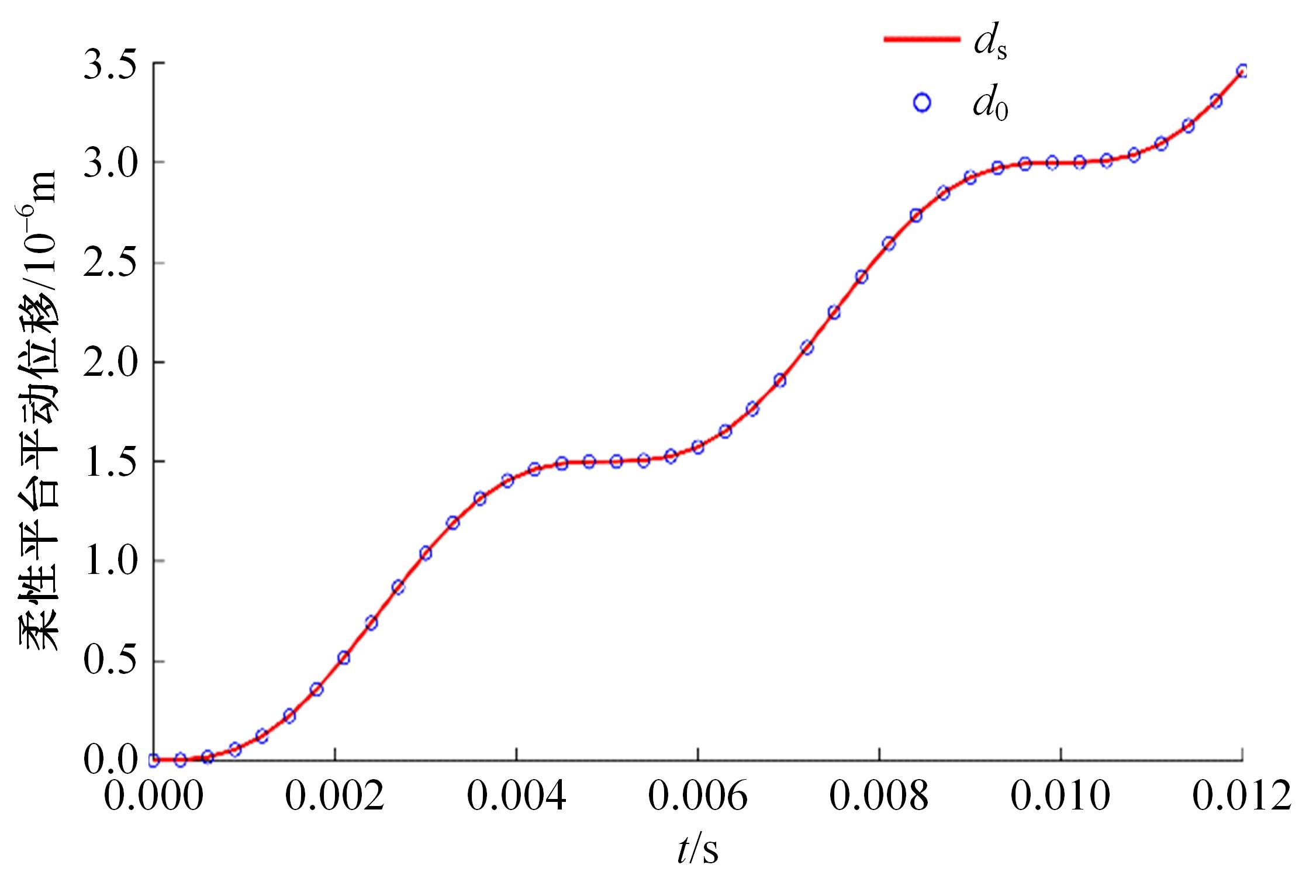
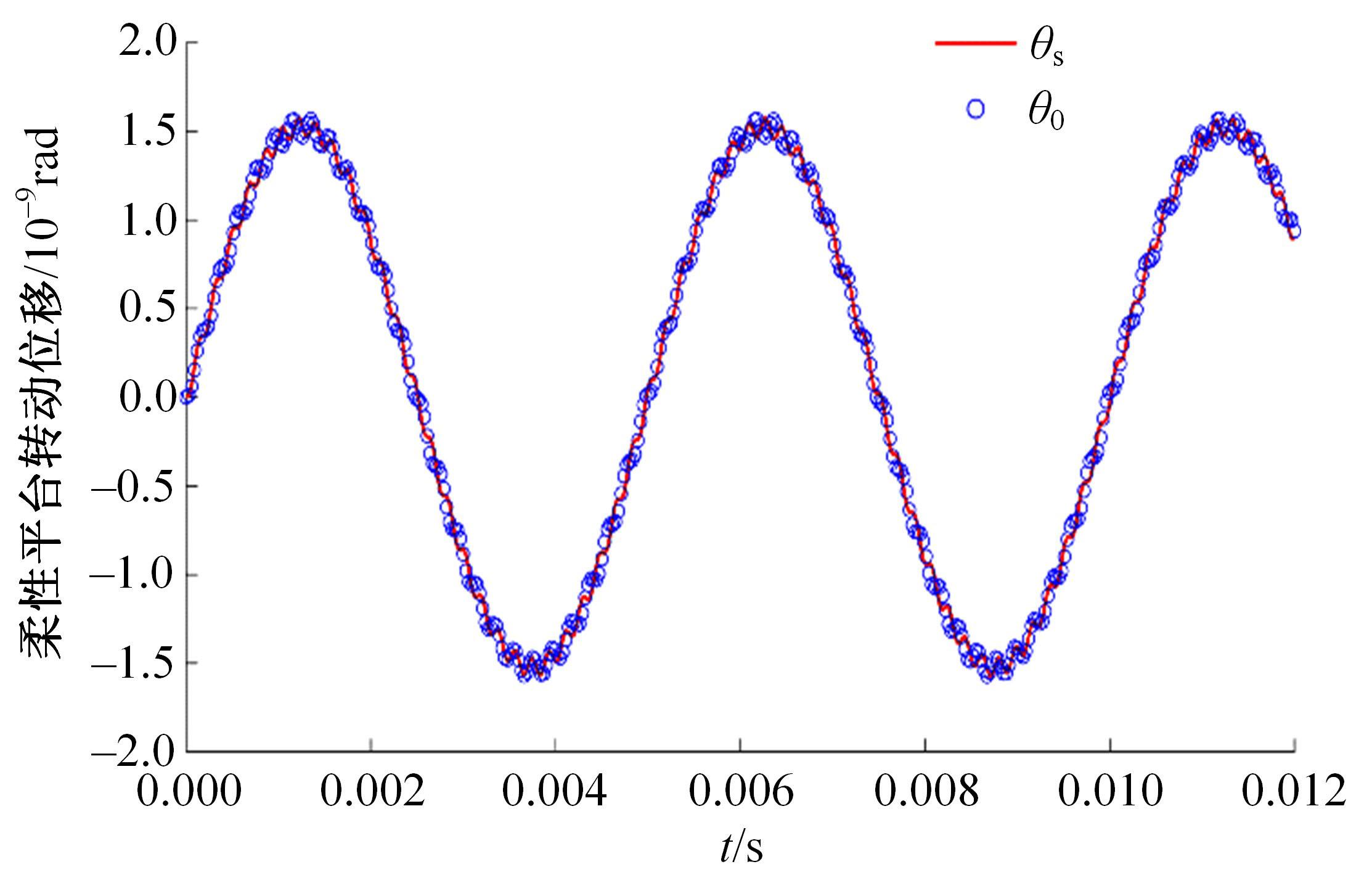
精密定位平台由于机械摩擦造成精度受限，难以满足大行程、高精度定位的运动要求。本文结合宏微复合结构，提出了一种单驱动刚柔耦合定位平台。相对于现有的宏微复合平台，大幅简化了机械结构和运动控制系统的设计。基于浮动坐标法和有限元法建立了单驱动刚柔耦合定位平台的静力学和动力学模型，并与商业软件ABAQUS及简化解析模型的分析结果进行对比，最大相对误差分别为1.6%和3.72%，证明了该理论模型具有较高的预测精度，可为刚柔耦合平台的优化设计及精密运动控制提供参考。

关键词: 机械工程, 刚柔耦合动力学, 有限元分析, 柔性铰链, 定位平台

Abstract:

The precision of traditional precision positioning stages are limited due to mechanical friction， so it is difficult to meet the motion requirements of large stroke and high precision. In this paper， a single drive rigid-flexible coupling positioning stage combined with macro- micro composite structure was proposed. Compared with the other macro-micro composite stage， it greatly simplified the design of mechanical structure and motion control system. Based on the floating coordinate method and finite element method， the static and dynamic model of the single drive rigid-flexible coupling positioning stage was established. The analysis results of these models were compared with the static analysis results of ABAQUS finite element software and the analytical solution of the simplified dynamic model， the maximum relative errors were 1.6% and 3.72% respectively. It is proved that this theoretical model has high prediction accuracy， which can provide parameters for the optimal design and precision motion control of the single drive rigid-flexible coupling stage.

Key words: mechanical engineering, rigid-flexible coupling dynamics, finite element analysis, flexure hinge, positioning stage

中图分类号:

TH113.1

杨志军,张驰,黄观新. 基于浮动坐标法的刚柔耦合定位平台力学模型[J]. 吉林大学学报(工学版), 2024, 54(2): 385-393.

Zhi-jun YANG,Chi ZHANG,Guan-xin HUANG. Mechanical model of rigid⁃flexible coupling positioning stage based on floating coordinate method[J]. Journal of Jilin University(Engineering and Technology Edition), 2024, 54(2): 385-393.

图/表 14

图1

图2

图3

图4

图5

表1

平台的质量参数"

平台类型	质量/kg
柔性平台	2.2625
刚性平台 $c 1$	0.0974
刚性平台 $c 2$	0.0974
刚性平台 $c 3$	0.0974
刚性平台 $c 4$	0.0974

表1

表2

柔性铰链的材料参数"

柔性铰链类型

杨氏模量E/Gpa

剪切模量G/Gpa

泊松比

$υ$

长度

$l$ /mm

厚度

$t$ /mm

宽度

$w$ /mm

直角

26.9

0.330

1.0

簧片

211

81.9

0.288

0.4

表2

图6

表3

表4

刚度误差（转动）"

工作方向	转动/ rad	k_ZA/ （N?m·rad^-1）	k_ZM/ （N?m·rad^-1）	误差/%
$θ X$	1.19E-7	8.43E7	8.43E7	0.05
$θ Y$	1.44E-7	6.93E7	6.91E7	0.14
$θ Z$	2.92E-7	3.43E7	3.38E7	1.60

表4

图7

表5

简化模型参数"

参数	物理意义
$m f$	刚性平台的质量
$m s$	柔性平台的质量
$J s$	柔性平台的转动惯量
$K r$	刚柔耦合平台绕X轴方向转动刚度
$K t$	刚柔耦合平台沿Y轴方向平动刚度
$d s$	柔性平台相对于惯性坐标系沿Y轴方向的平动位移
$Δ d f$	刚性平台相对于浮动坐标系沿Y轴方向的平动位移
$θ s$	柔性平台绕惯性坐标系X轴方向的转动位移
$F f$	刚性平台受到Y轴方向的集中力
$F s$	柔性平台受到Y轴方向的集中力
$M s$	柔性平台受到X轴方向的集中力矩

表5

图8

图9

参考文献 21

1	Kerschner R K. Differential motor drive for an XY stage[P].USA:
2	Mao J, Tachikawa H, Shimokohbe A. Precision positioning of a DC-motor-driven aerostatic slide system[J]. Precision Engineering, 2003, 27(1): 32-41.
3	Shinno H, Hashizume H, Yoshioka H, et al. X-Y-θ nano-positioning table system for a mother machine[J]. CIRP Annals-Manufacturing Technology, 2004, 53(1): 337-340.
4	王延风. 磁悬浮精密定位工作台机电一体化CAD/CAE集成研究[D]. 长春: 中国科学院长春光学精密机械与物理研究所, 2004.
	Wang Yan-feng. Research on the magnetic levitation precision stage with mechachonics CAD/CAE[D]. Changchun: Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, 2004.
5	Sharon A, Hogan N, Hardt D E. High bandwidth force regulation and inertia reduction using a macro/micro manipulator system[C]∥IEEE International Conference on Robotics & Automation, Pennsylvania, USA, 1988: 3247374.
6	于靖军, 裴旭, 毕树生, 等. 柔性铰链机构设计方法的研究进展[J]. 机械工程学报, 2010, 46(13): 2-13.
	Yu Jing-jun, Pei Xu, Bi Shu-sheng, et al. State-of-arts of design method for flexure mechanisms[J]. Journal of Mechanical Engineering, 2010, 46(13): 2-13.
7	曲兴田, 董景石, 郭俊臣, 等. 基于柔性铰链放大的压电叠堆泵[J]. 吉林大学学报:工学版, 2008, 38(3): 552-556.
	Qu Xing-tian, Dong Jing-shi, Guo Jun-chen, et al. Piezoelectric stack pump based on flexure hinge magnification[J]. Journal of Jilin University (Engineering and Technology Edition), 2008, 38(3): 552-556.
8	Uchino K. Ceramic actuators: principles and applications[J]. MRS Bulletin, 1993, 18(4): 42-48.
9	朱军辉. 全压电驱动的二维大行程纳米定位平台研究[D]. 苏州: 苏州大学机电工程学院, 2015.
	Zhu Jun-hui. Research on 2-DOF long stroke nano-positioning stage driven by hybrid piezoelectric actuators[D]. Suzhou: College of Mechanical and Electrical Engineering, Suzhou University, 2015.
10	Juhász L, Maas J, Borovac B. Parameter identification and hysteresis compensation of embedded piezoelectric stack actuators[J]. Mechatronics, 2011, 21(1): 329-338.
11	张涛, 孙立宁, 蔡鹤皋. 压电陶瓷基本特性研究[J]. 光学精密工程, 1998, 6(5): 27-31.
	Zhang Tao, Sun Li-ning, Cai He-gao. Study on the fundamental characteristics of piezoelectric element[J]. Optics and Precision Engineering, 1998, 6(5): 27-31.
12	Kawashima K, Arai T, Tadano K, et al. Development of coarse/fine dual stage using pneumatically driven bellows actuator and cylinder with air bearings[J]. Precision Engineering, 2010, 34(3):526-533.
13	Shinno H, Yoshioka H, Sawano H. A newly developed long range positioning table system with a sub-nanometer resolution[J]. CIRP Annals-Manufacturing Technology, 2011, 60(1): 403-406.
14	杨志军, 高忠义, 王丽君, 等. 面向刚柔耦合定位平台的模型预测控制算法[J]. 吉林大学学报: 工学版, 2022, 52(12): 2806-2815.
	Yang Zhi-jun, Gao Zhong-yi, Wang Li-jun, et al. Model predictive control algorithm for rigid-flexible coupling positioning stage[J]. Journal of Jilin University (Engineering and Technology Edition), 2022, 52(12): 2806-2815.
15	胡俊峰, 徐贵阳. 四种不同柔性铰链的三自由度微定位平台性能比较[J]. 机械设计与制造, 2014(2): 127-129.
	Hu Jun-feng, Xu Gui-yang. Characteristics comparison of a 3-DOF micro positioning stage with four different flexible hinges[J]. Machinery Design & Manufacture, 2014(2): 127-129.
16	Li R, Yang Z, Cai B, et al. A compliant guiding mechanism utilizing orthogonally oriented flexures with enhanced stiffness in degrees-of-constraint[J]. Mechanism and Machine Theory, 2022, 167: 104555.
17	吴胜宝, 章定国. 大范围运动刚体-柔性梁刚柔耦合动力学分析[J]. 振动工程学报, 2011, 24(1):1- 7.
	Wu Sheng-bao, Zhang Ding-guo. Rigid-flexible coupling dynamic analysis of hub-flexible beam with large overall motion[J]. Journal of Vibration Engineering, 2011, 24(1): 1-7.
18	刘铸永. 刚-柔耦合系统动力学建模理论与仿真技术研究[D]. 上海: 上海交通大学船舶海洋与建筑工程学院, 2008.
	Liu Zhu-yong. Study on modeling theory and simulation technique for rigid-flexible coupling systems dynamics[D]. Shanghai: School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, 2008.
19	丁楠. 柔性多体系统动力学建模方法研究[D]. 长春: 吉林大学数学学院, 2013.
	Ding Nan. Studies on modeling of flexible multi-body system dynamics[D]. Changchun: School of Mathematics, Jilin University, 2013.
20	李彬, 刘锦阳, 洪嘉振. 计及剪切变形的Timoshenko梁的刚-柔耦合动力学[J]. 计算力学学报, 2006, 23(4): 419-422.
	Li Bin, Liu Jin-yang, Hong Jia-zhen. Coupling dynamics of Timoshenko beam with shear deformation[J]. Chinese Journal of Computational Mechanics, 2006, 23(4): 419-422.
21	张军锋, 尹会娜, 孙大勇, 等. 基于形函数推导考虑剪切变形的欧拉梁单元刚度矩阵[J]. 重庆交通大学学报:自然科学版, 2020, 39(9): 59-66.
	Zhang Jun-feng, Yin Hui-na, Sun Da-yong, et al. Euler beam element stiffness matrix considering shear deformation based on shape function derivation[J]. Journal of Chongqing Jiaotong University (Natural Science), 2020, 39(9): 59-66.

相关文章 15

[1]	石林榕,赵武云. 西北寒旱农区胡麻滚勺式精量穴播器的设计及试验[J]. 吉林大学学报(工学版), 2023, 53(9): 2706-2717.
[2]	柴博森,王广义,闫东,朱国仁,张进,吕恒升. 液力变矩器空化数值模拟及对性能的影响[J]. 吉林大学学报(工学版), 2023, 53(8): 2236-2244.
[3]	陈国辉,徐业银,焦映厚. 考虑偏转的斜齿轮啮合刚度及其振动分析[J]. 吉林大学学报(工学版), 2023, 53(7): 1902-1910.
[4]	陈贵升,罗国焱,李靓雪,黄震,李一. 柴油机颗粒捕集器孔道流场及其高原环境下噪声特性分析[J]. 吉林大学学报(工学版), 2023, 53(7): 1892-1901.
[5]	于立娟,安阳,何佳龙,李国发,王升旭. 机电装备载荷谱外推技术研究进展及发展趋势[J]. 吉林大学学报(工学版), 2023, 53(4): 941-953.
[6]	李胜,朱佳,黄德惠,陈存福,费洪庆,丰伟,胡兴军. 空冷中冷器百叶窗翅片结构参数优化[J]. 吉林大学学报(工学版), 2023, 53(4): 998-1006.
[7]	王建,于威,王斌. 高原状态下甲醇替代率对柴油机燃烧与排放的影响[J]. 吉林大学学报(工学版), 2023, 53(4): 954-963.
[8]	柴博森,闫东,王广义,左文杰. 制动工况桃腔偶合器三维涡特征分析及仿真评价[J]. 吉林大学学报(工学版), 2023, 53(11): 3045-3055.
[9]	肖阳,王洁,刘孟军,杨发庆,张天瑶,兰巍. 质子交换膜燃料电池气体扩散层的力学改进模型[J]. 吉林大学学报(工学版), 2022, 52(9): 2147-2155.
[10]	朱凌,王秋成. 空间几何约束下新能源汽车驱动系统协调控制方法[J]. 吉林大学学报(工学版), 2022, 52(7): 1509-1514.
[11]	金兆辉,谷乐祺,洪伟,解方喜,尤田. 液压可变气门系统压力波动的影响分析[J]. 吉林大学学报(工学版), 2022, 52(4): 773-780.
[12]	张岩,刘玮,张树勇,裴毅强,董蒙蒙,秦静. 二/四冲程可变柴油机燃烧室热负荷的改善[J]. 吉林大学学报(工学版), 2022, 52(3): 504-514.
[13]	李国发,王彦博,何佳龙,王继利. 机电装备健康状态评估研究进展及发展趋势[J]. 吉林大学学报(工学版), 2022, 52(2): 267-279.
[14]	杨志军,高忠义,王丽君,黄观新,危宇泰. 面向刚柔耦合定位平台的模型预测控制算法[J]. 吉林大学学报(工学版), 2022, 52(12): 2806-2815.
[15]	王磊,黄秉汉,丛家慧,回丽,周松,徐永臻. 超声冲击对搅拌摩擦焊缝疲劳性能的影响[J]. 吉林大学学报(工学版), 2022, 52(11): 2542-2548.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

工作方向	平动/m	k_PA/（N·m^-1）	k_PA/（N·m^-1）	误差/%
X	2.25E-9	4.44E9	4.39E9	1.19
Y	6.79E-8	1.47E8	1.47E8	0.33
Z	1.16E-9	8.60E9	8.59E9	0.13