基于Hopfield神经网络的单缸插销式伸缩臂伸缩路径优化

doi:10.13229/j.cnki.jdxbgxb20181272

摘要/Abstract

摘要：

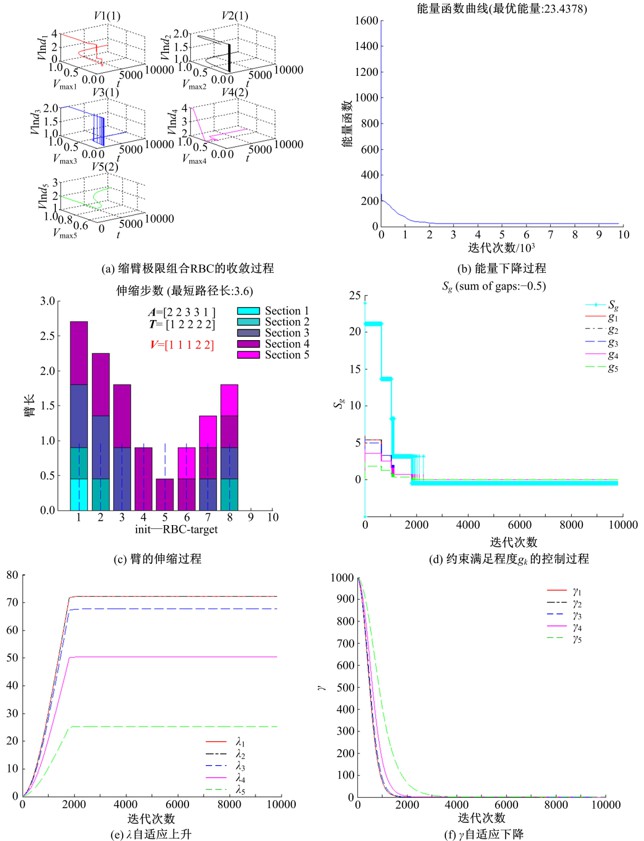
提出了单缸插销式伸缩臂伸缩路径优化问题，采用Hopfield神经网络构建了数学模型。由于能量方程中的约束项罚参数λ和目标项罚参数γ的确定往往相互矛盾：当λ占优时，能量方程更多朝向满足约束方向收敛，得到的有效解往往不是高质量解；当γ占优时，则可能收敛到无效解。为此，提出了λ为向上梯度递增、γ为向下梯度递减的曲线形式；对于λ和γ的增量确定，提出了一种基于约束边界偏差控制的PID自适应增量法，通过对约束边界偏差的PID控制使有效解的生成可控。实验结果表明：路径优化后伸缩效率能提升10%~30%。神经网络模型优化效果较好，几乎能100%收敛到有效解，同时由于PID控制使解聚集到约束边界，最优解生成率也较高，接近50%。

关键词: 机械设计, Hopfield神经网络, 单缸插销式伸缩臂, 伸缩路径优化, PID控制器

Abstract:

The issue of Telescoping Path Optimization (TPO) of Single-cylinder Pin-type Multi-section Boom (SPMB) was raised and its model is proposed by using Hopfield Neural Network (HNN). In an energy equation, it is difficult to balance the parameter λ of constrained term and the parameter γ of objective term. When λ dominates, network converges toward constraint satisfaction and a valid solution is often of poor quality. Whereas when γ dominates, network might converge to an invalid solution. To solve this problem, this paper proposes that the λ is gradient rising and the γ is gradient falling. A PID hybridized method based on Constraint Boundary Gap (CBG) control is presented to adaptively regulate the increments of λ and γ. Experimental results show that the telescoping efficiency improves 10%~30% after path optimization. TPO model achieves good optimization effect, and enables network converge almost 100% to a valid solution. The generation proportion of the optimal solution remains high at about 50% seeing that PID control often imposes a solution to the constraint boundary.

Key words: mechanical design, Hopfield neural network, single-cylinder pin-type multi-section boom, telescoping path optimization, proportional integral derivative(PID) controller

中图分类号:

TH213

毛艳,成凯. 基于Hopfield神经网络的单缸插销式伸缩臂伸缩路径优化[J]. 吉林大学学报(工学版), 2020, 50(1): 53-65.

Yan MAO,Kai CHENG. Telescoping path optimization of a single-cylinder pin⁃type multi⁃section boom based on Hopfield neural network[J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(1): 53-65.

图/表 8

图1

表1

表2

图2

表3

图3

表4

表5

参考文献 20

1	Zhan Chun-xin , Liu Quan , Guo Ji-mei , et al . Single-cylinder pin-type telescopic boom track optimized control method and control system[P]. WO/ 2011/038633, 2011-07-04.
2	毛艳, 成凯 . 一种高效的单缸插销式多级顺序伸缩路径优化方法[P]. 中国:CN 106744389B, 2018-07-17.
3	毛艳, 成凯 . 单缸插销式多级顺序伸缩路径优化方法 [P].中国:CN 106744386B, 2018-04-10.
4	郑飞 . 动态规划法在服装运输车辆路径优化中的应用研究[J]. 物流科技, 2016, 39(2): 78-82.
	Zheng Fei . Research on the application of dynamic programming method in the optimization of apparel vehicle routing[J]. Logistics Sci-Tech, 2016, 39(2): 78-82.
5	Wen U P , Lan K M , Shih H S . A review of hopfield neural networks for solving mathematical programming problems[J]. European Journal of Operational Research, 2009, 198(3): 675-687.
6	Hopfield J J . Neural networks and physical systems with emergent collective computational abilities[J]. Proceedings of the National Academy of Sciences, 1982, 79(8): 2554-2558.
7	Hopfield J J , Tank D W . ‘Neural’ computation of decisions in optimization problems[J]. Biological Cybernetics, 1985, 52(3): 141-152.
8	Wilson G V , Pawley G S . On the stability of the travelling salesman problem algorithm of Hopfield and tank[J]. Biological Cybernetics, 1988, 58(1): 63-70.
9	Kennedy M P , Chua L O . Neural networks for nonlinear programming[J]. IEEE Transactions on Circuits & Systems, 1988, 35(5): 554-562.
10	Rodriguez-Vazquez A , Rueda A , Huertas J L , et al . Switched-capacitor neural networks for linear programming[J]. Electronics Letters, 2002, 24(8): 496-498.
11	Brandt R D , Yao W , Laub A J , et al . Alternative networks for solving the traveling salesman problem and the list-matching problem[C]∥International Conference on Neural Networks, San Diego, CA, USA, 1988: 333-340.
12	Protzel P W , Palumbo D L , Arras M K . Performance and fault-tolerance of neural networks for optimization[J]. IEEE Transactions on Neural Networks, 1993, 4(4): 600-614.
13	Shirazi B , Yih S . Critical analysis of applying hopfield neural net model to optimization problems[C]∥IEEE International Conference on Systems, Man and Cybernetics, Cambridge,MA,USA, 1989: 210-215.
14	Aiyer S V B , Niranjan M , Fallside F . A theoretical investigation into the performance of the Hopfield model[J]. IEEE Transactions on Neural Networks, 1990, 1(2): 204-215.
15	孙守宇, 郑君里 . Hopfield 网络求解 TSP的一种改进算法和理论证明[J]. 电子学报, 1995, 23(1): 73-78.
	Sun Shou-yu , Zheng Jun-li . A modified algorithm and theoretical analysis for hopfield network solving TSP[J]. Acta Electronica Sinica, 1995, 23(1): 73-78.
16	张军英, 许进, 保铮 . 神经网络求解TSP问题的理论分析及其改进[J]. 西安电子科技大学学报, 1996, (增刊1): 88-98.
	Zhang Jun-ying , Xu Jin , Bao Zheng . Theoretical analysis and improvement of the neural network to solve the TSP problem[J]. Journal of Xidian University, 1996(Sup.1): 88-98.
17	Effati S , Jafarzadeh M . A new nonlinear neural network for solving a class of constrained parametric optimization problems[J]. Applied Mathematics & Computation, 2007, 186(1): 814-819.
18	Lemonge A C C , Barbosa H J C , Bernardino H S . Variants of an adaptive penalty scheme for steady-state genetic algorithms in engineering optimization[J]. Engineering Computations, 2015, 32(8): 2182-2215.
19	Schoenauer M , Michalewicz Z . Boundary operators for constrained optimization problems[C]∥Baeck T, ed. Proceedings of the 7th International Conference on Genetic Algorithms. San Mateo, CA: Morgan Kaufmann Publishers, 1997. 322-329.
20	Wang Y , Cai Z , Guo G , et al . Multiobjective optimization and hybrid evolutionary algorithm to solve constrained optimization problems[J]. IEEE Transactions on Systems, Man, and Cybernetics, 2007: 37(3): 560-575.

相关文章 15

[1]	贾富淳,孟宪皆,雷雨龙. 基于多目标遗传算法的二自由度动力吸振器优化设计[J]. 吉林大学学报(工学版), 2019, 49(6): 1969-1976.
[2]	谢志江,王昆,皮阳军,吴小勇,郭映位. 新的6⁃PSS型并联机构正向运动学求解方法[J]. 吉林大学学报(工学版), 2019, 49(6): 1977-1985.
[3]	曹恩国,刘坤,吉硕,孙震源,徐洪伟,骆星吉. 减重站起康复训练系统机械结构设计与优化[J]. 吉林大学学报(工学版), 2019, 49(5): 1558-1566.
[4]	李俊烨,刘洋,卢慧,孟文卿,杨兆军,张心明. 基于分子动力学的磨粒微切削单晶铁数值分析[J]. 吉林大学学报(工学版), 2019, 49(5): 1567-1574.
[5]	张艳芹,冯雅楠,孔鹏睿,于晓东,孔祥滨. 基于热油携带的静压支承油膜温度场及试验[J]. 吉林大学学报(工学版), 2019, 49(4): 1203-1211.
[6]	杨成,赵永胜,刘志峰,蔡力钢. 基于多尺度理论的栓接结合部动力学建模[J]. 吉林大学学报(工学版), 2019, 49(4): 1212-1220.
[7]	王家序,倪小康,韩彦峰,向果,肖科. 轴向往复运动下微槽轴承混合润滑数值模型[J]. 吉林大学学报(工学版), 2019, 49(3): 888-896.
[8]	王兴野,张进秋,李国强,彭志召. 惯性质量对齿轮齿条式作动器阻尼特性的影响[J]. 吉林大学学报(工学版), 2019, 49(3): 881-887.
[9]	刘坤,吉硕,孙震源,徐洪伟,刘勇,赵静霞. 多功能坐站辅助型如厕轮椅机械结构设计与优化[J]. 吉林大学学报(工学版), 2019, 49(3): 872-880.
[10]	毕秋实,王国强,黄婷婷,毛瑞,鲁艳鹏. 基于DEM-FEM耦合的双齿辊破碎机辊齿强度分析[J]. 吉林大学学报(工学版), 2018, 48(6): 1770-1776.
[11]	朱伟,王传伟,顾开荣,沈惠平,许可,汪源. 一种新型张拉整体并联机构刚度及动力学分析[J]. 吉林大学学报(工学版), 2018, 48(6): 1777-1786.
[12]	刘建芳, 王记波, 刘国君, 李新波, 梁实海, 杨志刚. 基于PMMA内嵌三维流道的压电驱动微混合器[J]. 吉林大学学报(工学版), 2018, 48(5): 1500-1507.
[13]	毛宇泽, 王黎钦. 鼠笼支撑一体化结构对薄壁球轴承承载性能的影响[J]. 吉林大学学报(工学版), 2018, 48(5): 1508-1514.
[14]	王涛, 伞晓刚, 高世杰, 王惠先, 王晶, 倪迎雪. 光电跟踪转台垂直轴系动态特性[J]. 吉林大学学报(工学版), 2018, 48(4): 1099-1105.
[15]	谢传流, 汤方平, 孙丹丹, 张文鹏, 夏烨, 段小汇. 立式混流泵装置压力脉动的模型试验分析[J]. 吉林大学学报(工学版), 2018, 48(4): 1114-1123.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

步数	实例A				实例B
步数	未优化	臂节	优化后	臂节	未优化	臂节	优化后	臂节
0	1 4 4 1 1	——	1 4 4 1 1	——	2 2 2 2 2	——	2 2 2 2 2	——
1	1 1 4 1 1	II	1 1 4 1 1	II	1 2 2 2 2	I	1 2 2 2 2	I
2	1 1 1 1 1	III	1 1 2 1 1	III	1 1 2 2 2	II	1 1 2 2 2	II
3	1 1 1 1 2	V	1 1 2 1 2	V	1 1 1 2 2	III	1 1 2 1 2	IV
4	1 1 1 2 2	IV	1 1 2 2 2	IV	1 1 1 1 2	IV	2 1 2 1 2	I
5	1 1 2 2 2	III	1 2 2 2 2	II	1 1 2 1 2	III
6	1 2 2 2 2	II	2 2 2 2 2	I	2 1 2 1 2	I
7	2 2 2 2 2	I

HNN γ参数恒定,γ=常数	HNN γ定常数衰减;Δγ= K_γ ·γ(t)	HNN γ PID;Δγ见式（5）
B=5, C=5	B=5, C=5	B=5, C=5
μ=μ_γ = 0.000 1	μ_λ =μ_γ =0.000 1	μ_λ =μ_γ =0.000 1
K _p _λ =10,K _i _λ =0.1,K _d _λ =1	K _p _λ =10,K _i _λ =0.1,K _d _λ =1	K _p _λ =10,K _i _λ =0.1,K _d _λ =1
γ=[1010101010]	K_γ =10	K _p _γ =0.1,K _i _γ =0.01, K _d _γ =1
λ(0)=0	λ(0)=0,γ(0)=1 000	λ(0)=0,γ(0)=1 000

	工况
算法	n=5， A =[21212] T =[23221]		n=6， A =[212121] T =[233221]		n=8， A =[21212121] T =[23333221]		n=10， A =[2121212121] T =[2333333221]
算法	有效解比 /最优解比	t/s	有效解比 /最优解比	t/s	有效解比 /最优解比	t/s	有效解比 /最优解比	t/s
排列组合	100% /100%	0.012	100% /100%	0.012	100% /100%	0.036	100% /100%	0.168
动态规划	100% /100%	0.053	100% /100%	0.059	-	-	-	-
HNN	90% /50%	0.519	90% /40%	0.640	80% /30%	0.641	80% /10%	0.632

	工况
算法	n=5， A =[22222] T =[21212]		n=6， A =[222222] T =[212121]		n=6， A =[22222222] T =[21212121]		n=10， A =[2222222222] T =[2121212121]
算法	有效解比 /最优解比	t/s	有效解比 /最优解比	t/s	有效解比	t/s	有效解比 /最优解比	t/s
排列组合	100% /100%	0.014	100% /100%	0.014	100% /100%	0.016	100% /100%	0.035
动态规划	100% /100%	0.053	100% /100%	0.059	--	--	--	--
HNN	100% /30%	0.634	90% /80%	0.639	100% /80%	0.635	90% /60%	0.637