钢纤维混凝土组合桥面板负弯矩区开裂性能试验

doi:10.13229/j.cnki.jdxbgxb.20211393

摘要/Abstract

摘要：

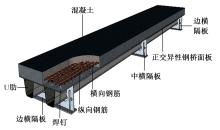
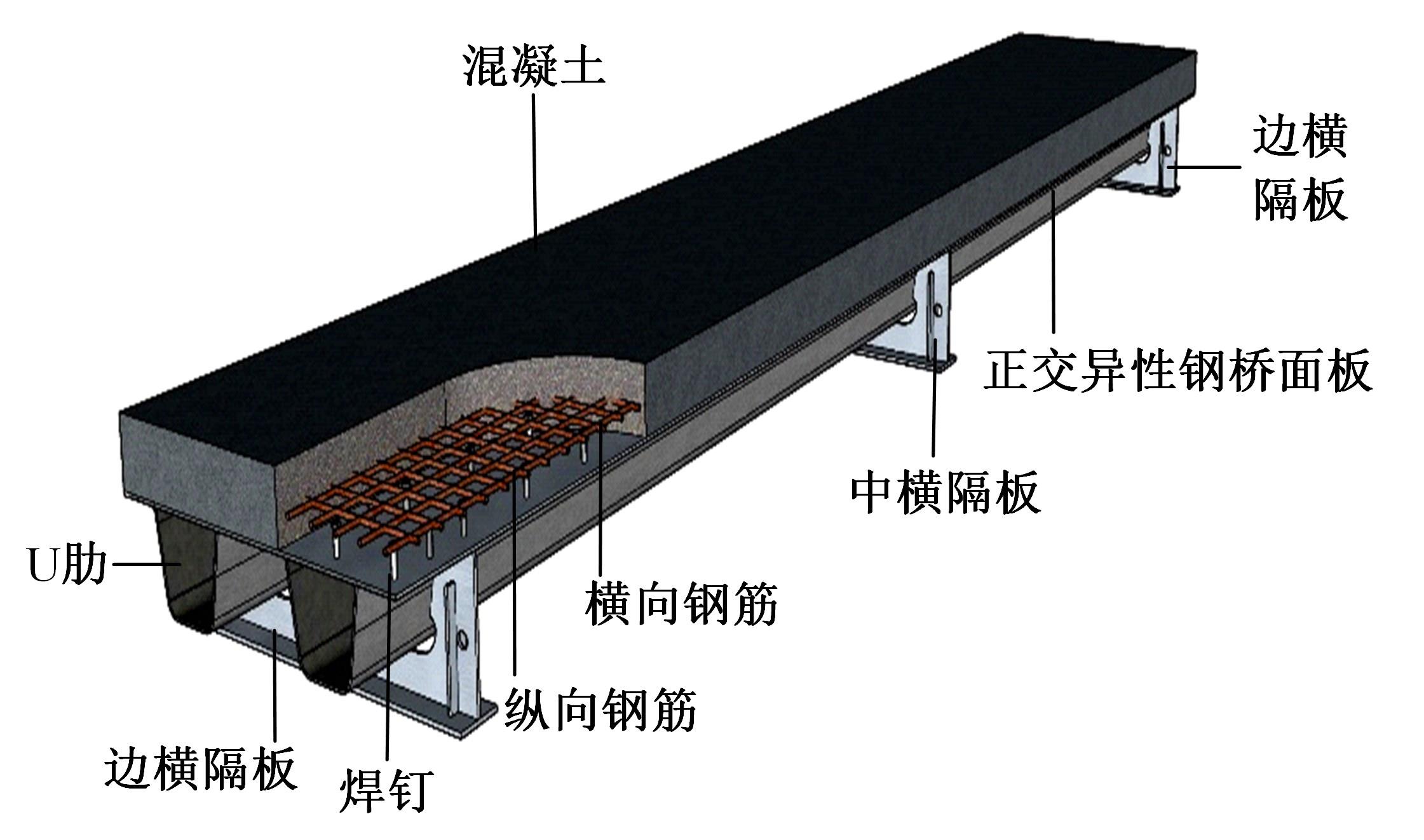
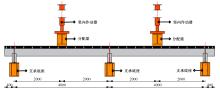
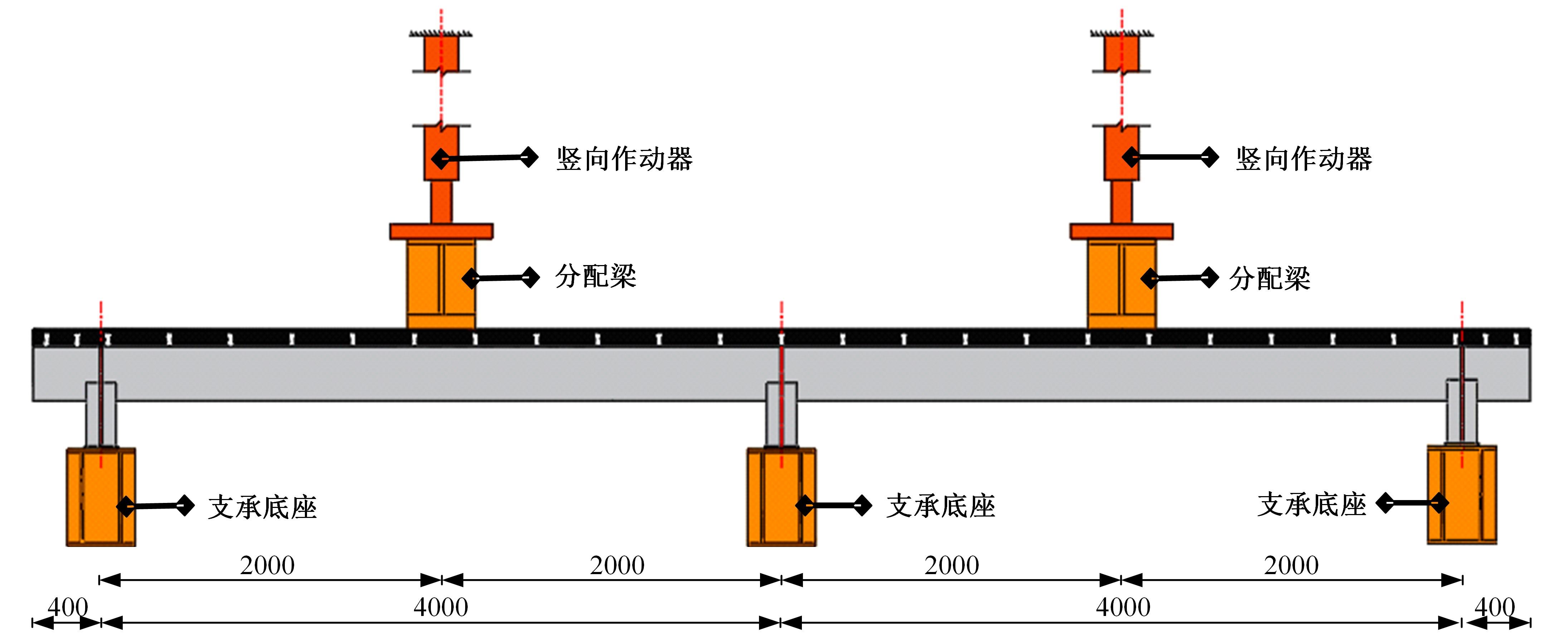
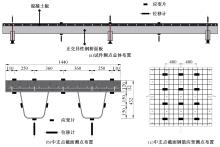
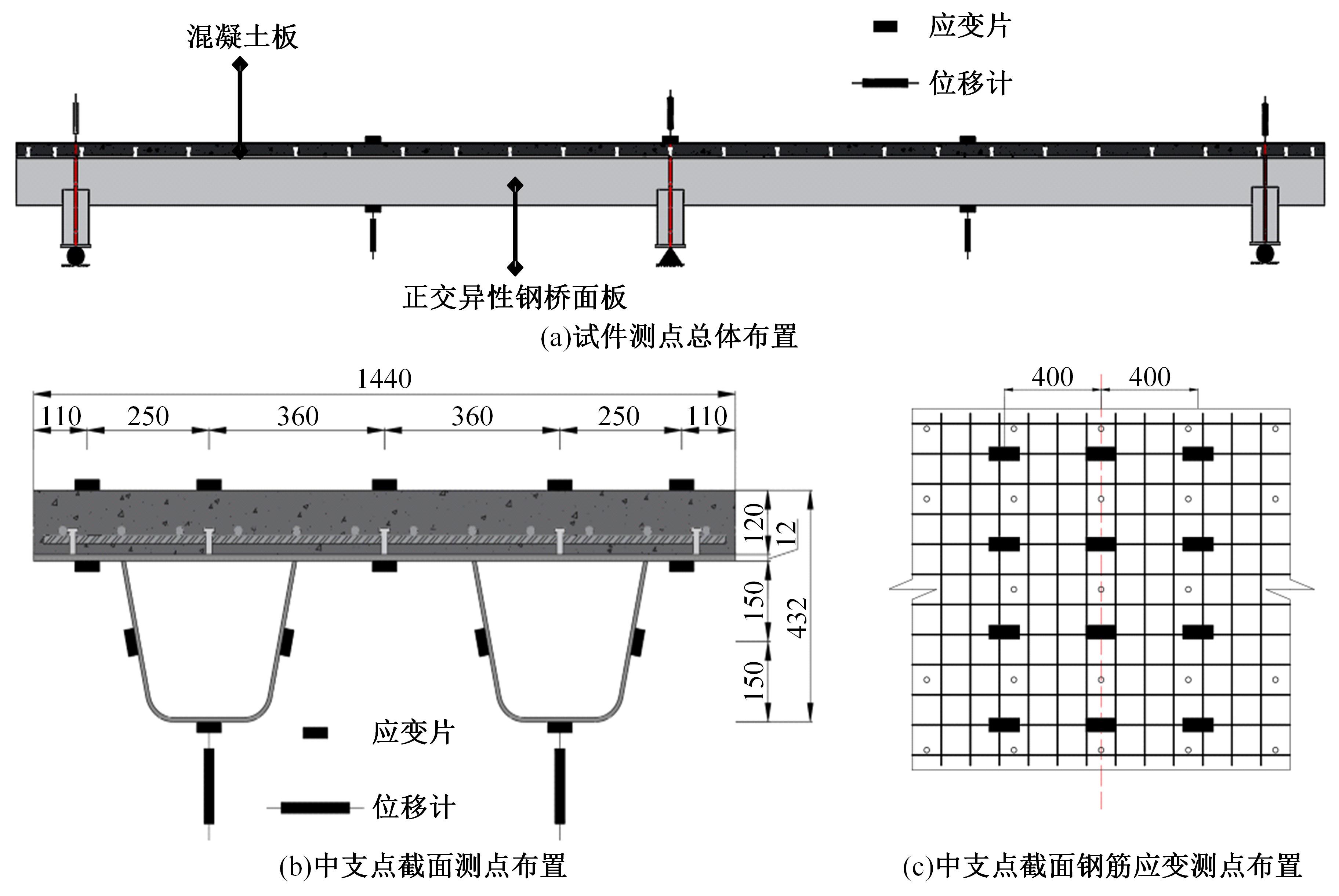
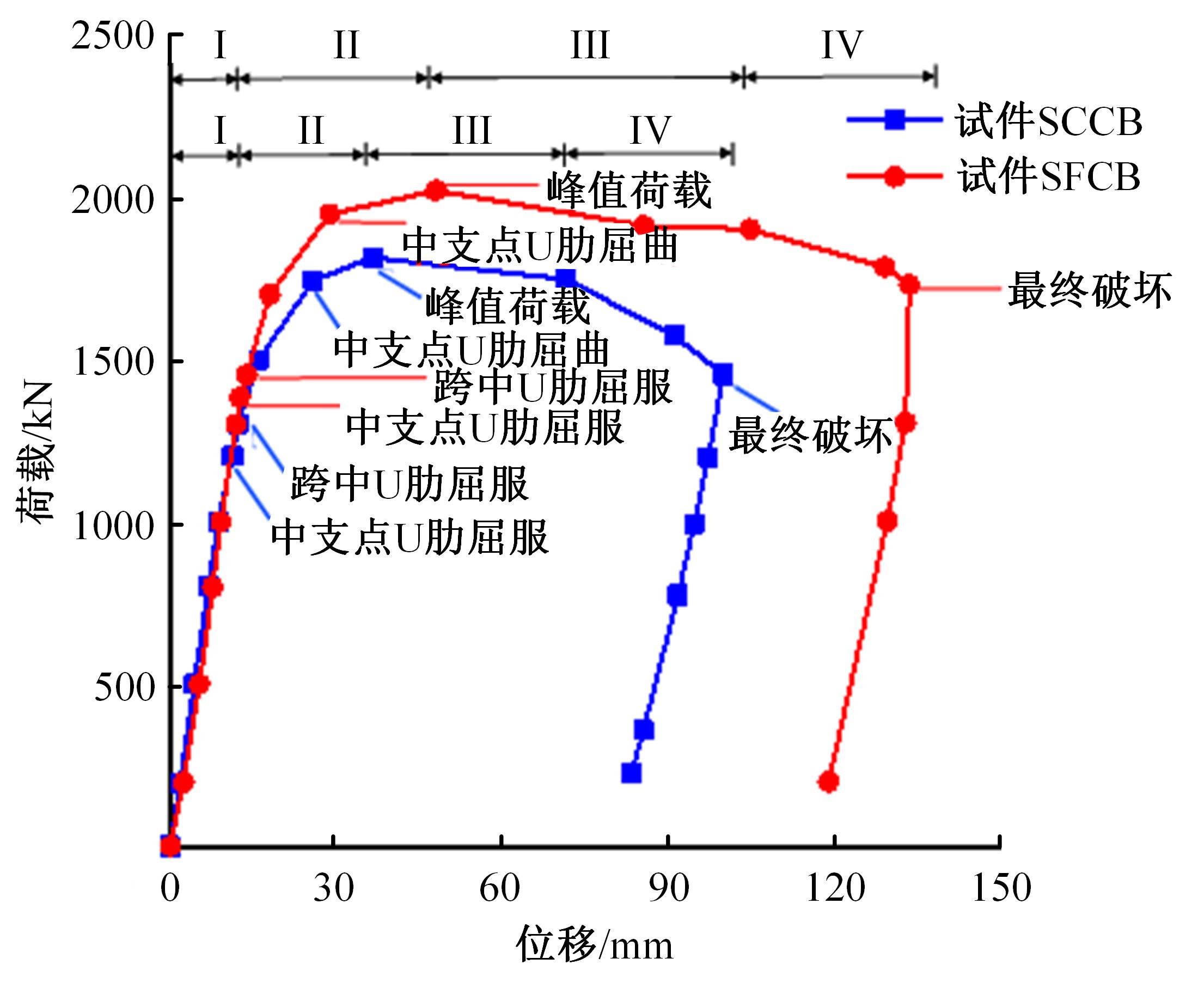
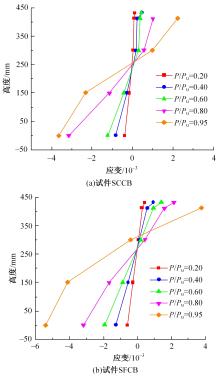
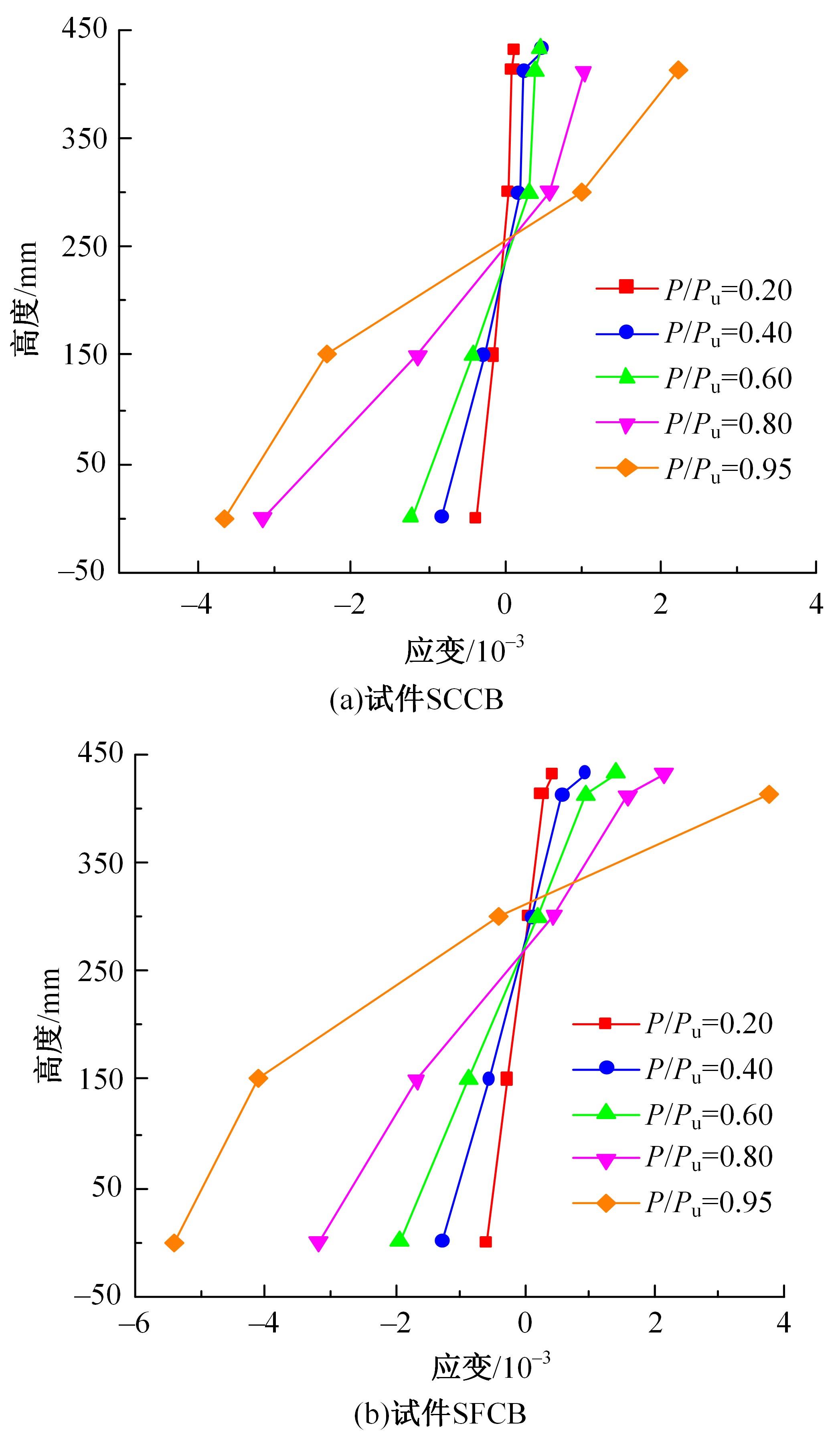
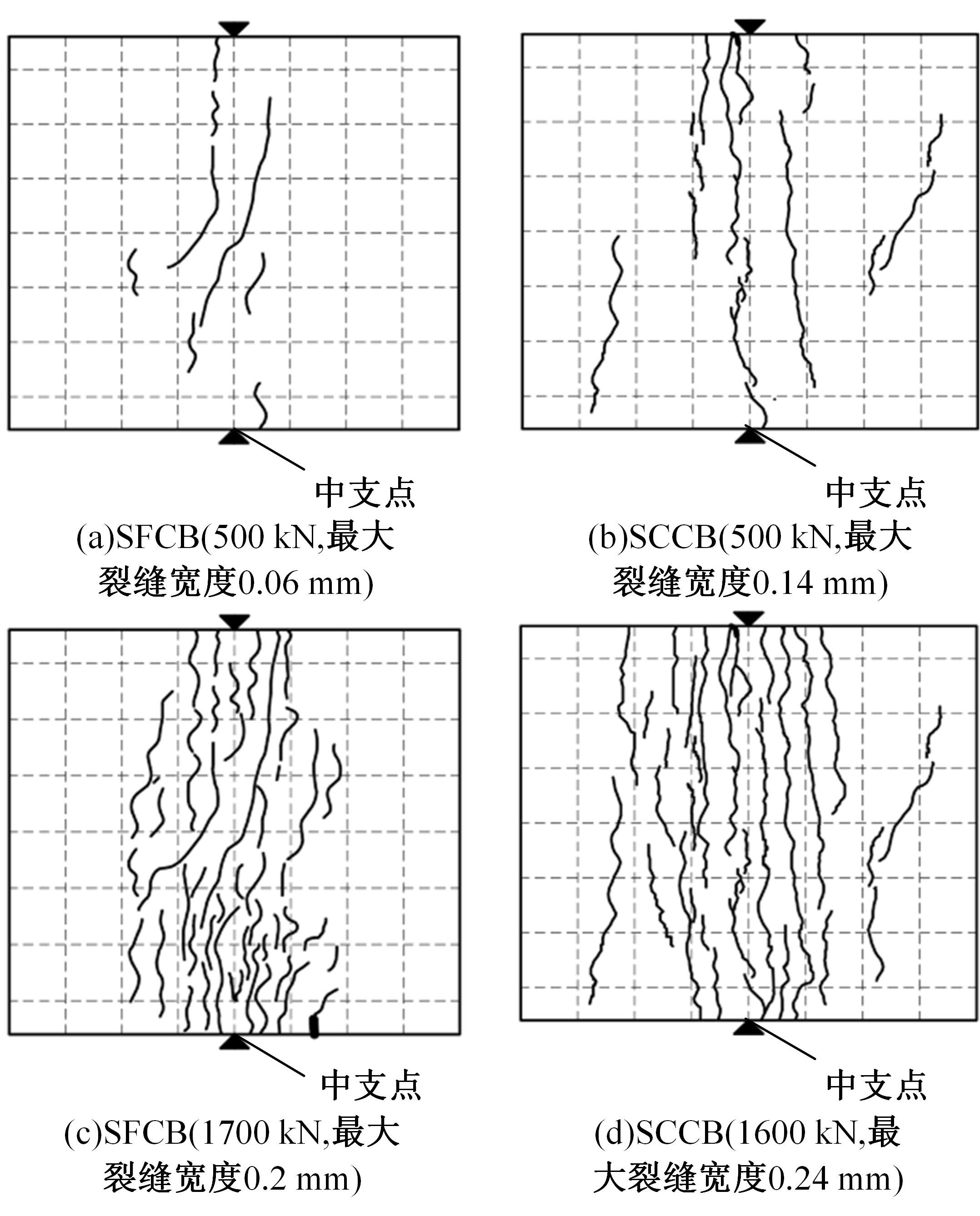
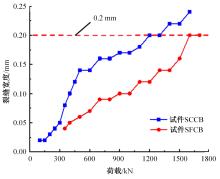
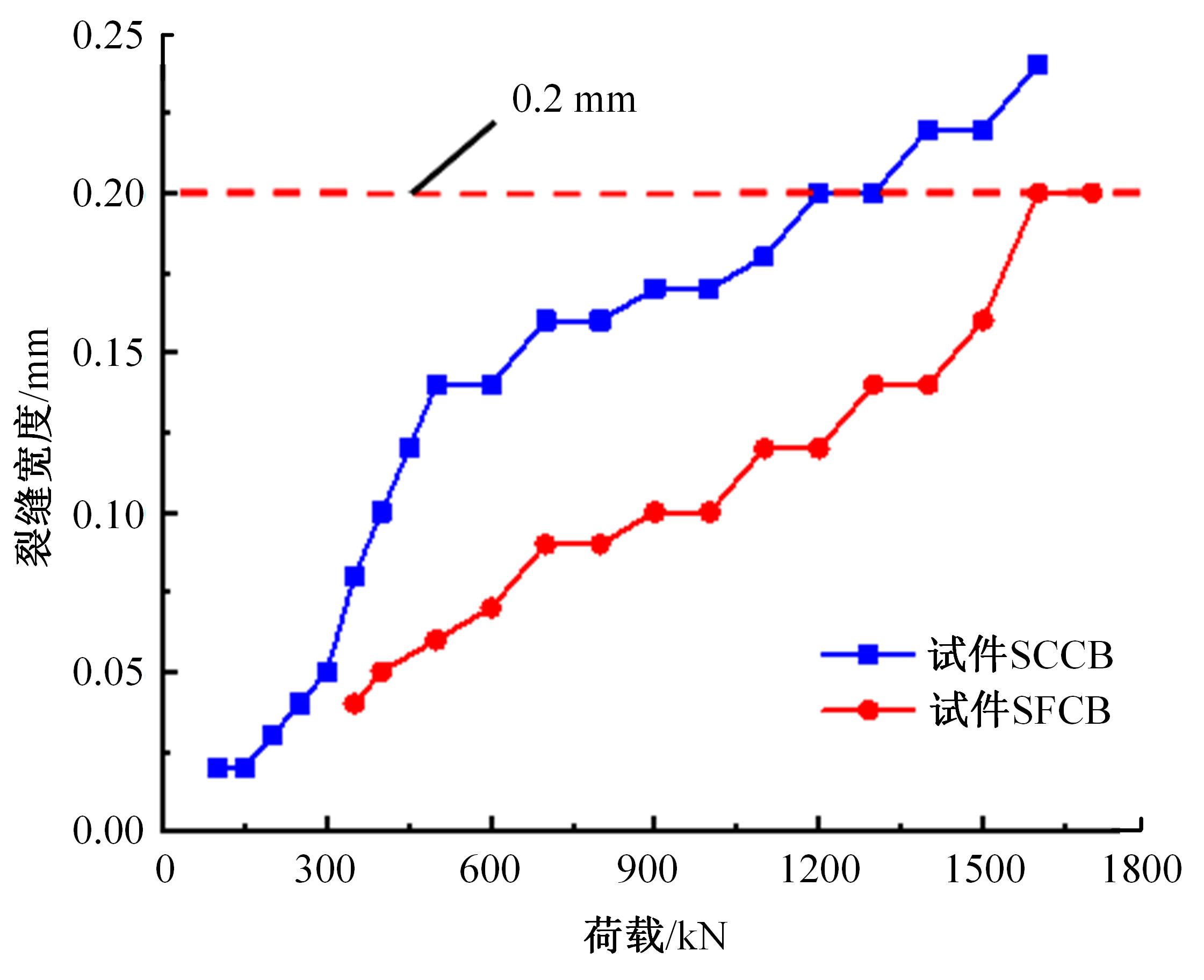
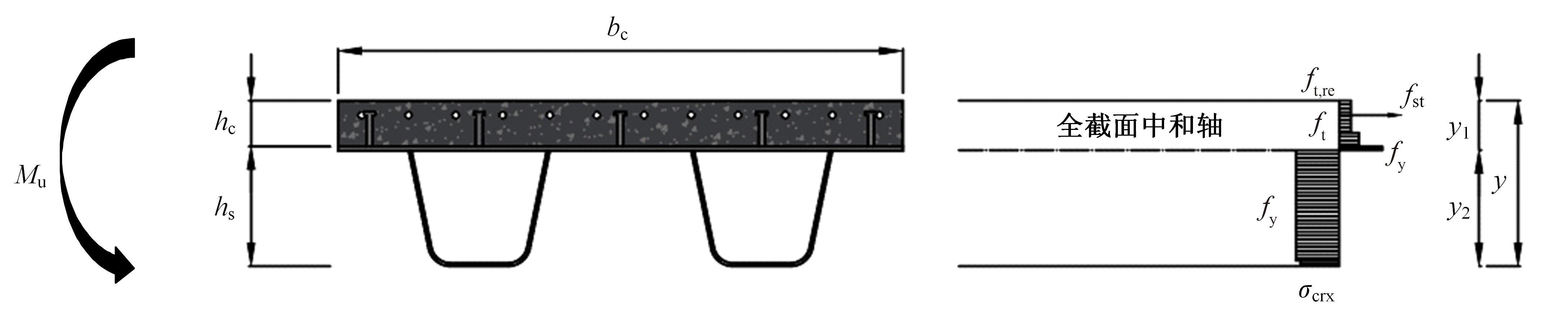
为研究正交异性钢-钢纤维混凝土组合桥面板的受力性能，特别是钢纤维混凝土对组合桥面板负弯矩区开裂性能的影响，设计制作了2个正交异性钢-混组合桥面板，其中一个是常规C60混凝土（NC）组合桥面板，另一个是钢纤维混凝土（SFRC）组合桥面板，进行了组合桥面板的静力试验。测试了在不同荷载下两个试件的变形、不同截面上的应变、混凝土的裂缝宽度、破坏形态以及极限承载力等。试验结果表明：钢-SFRC组合桥面板初始开裂弯矩与极限弯矩均显著大于钢-NC组合桥面板；①同钢-NC组合桥面板相比，采用SFRC的桥面板试件在弯矩作用下，中支点处混凝土开裂范围减少一半，且裂缝呈现为“细而密”的特征；两试件在受弯破坏极限状态下，均表现为中支点区域下部U肋屈曲变形及上部混凝土开裂；②基于先行规范中组合结构抗弯承载力计算公式提出了考虑钢纤维混凝土开裂后残余强度的抗弯承载力计算方法，该方法所得计算值同试验值吻合较好，可有效预测正交异性钢-SFRC组合桥面板的抗弯承载力，可有效预测正交异性钢-SFRC组合桥面板的抗弯承载力，为实际工程应用提供了理论参考。

关键词: 桥梁工程, 组合桥面板, 负弯矩区, 裂缝宽度, 试验研究

Abstract:

In order to study the stressing performance of steel-steel fiber reinforced concrete composite bridge deck， especially the influence of steel fiber reinforced concrete on the concrete cracking performance of the bridge deck in the negative moment region of the composite bridge deck. Two orthotropic composite bridge decks were designed and manufactured， one of which was a conventional C60 concrete composite bridge deck and other was a steel fiber reinforced concrete composite bridge deck. The static tests of two composite bridge deck were carried out. The experiment tested the deformation of two bridge decks under different loads， the strain of each member on different sections， the width of concrete cracks， the failure mode and the ultimate load carrying capacity. The existing standard formula for flexural bearing capacity of composite bridge decks was amended， and a recommended formula for flexural bearing capacity considering the residual strength of steel fiber reinforced concrete after cracking was proposed. The tests show that the initial cracking load of the steel-steel fiber reinforced concrete composite bridge deck are 3.5 times higher than those of the conventional C60 concrete composite bridge deck respectively. Using steel fiber reinforced concrete instead of conventional C60 concrete as the composite bridge deck can greatly improve the cracking resistance of the concrete in the negative moment region of the orthotropic composite bridge deck. At the same time， the proposed formula has high accuracy and can effectively predict the flexural bearing capacity of the orthotropic steel-SFRC composite bridge deck， providing a theoretical reference for practical engineering applications.

Key words: bridge engineering, composite bridge deck, negative moment region, crack width, experimental studies

中图分类号:

TU398

曾明根,武彧,苏庆田. 钢纤维混凝土组合桥面板负弯矩区开裂性能试验[J]. 吉林大学学报(工学版), 2023, 53(11): 3176-3185.

Ming-gen ZENG,Yu WU,Qing-tian SU. Experimental studies on cracking behavior of steel fiber reinforced concrete slab in negative moment region of orthotropic composite bridge deck[J]. Journal of Jilin University(Engineering and Technology Edition), 2023, 53(11): 3176-3185.

图/表 14

图1

图2

图3

表1

图4

表2

图5

图6

图7

图8

表3

图9

表4

图10

参考文献 24

1	杨义东,李涛. 钢-混凝土组合结构桥在日本的发展趋势[J]. 国外桥梁,1998(4):39-42.
	Yang Yi-dong, Li Tao. The trend of the steel-concrete composite bridge in Japan[J]. World Bridges, 1998(4): 39-42.
2	吴冲. 现代钢桥[M]. 北京:人民交通出版社,2006.
3	Orta L, Bartlett F M. Reliability analysis of concrete deck overlays[J]. Structural Safety, 2015, 56: 30-38.
4	Su N Y, Lou L W, Amirkhanian A, et al. Assessment of effective patching material for concrete bridge deck—a review[J]. Construction and Building Materials, 2021, 293: 123520.
5	Shiotani T, Ohtsu H, Momoki S, et al. Damage evaluation for concrete bridge deck by means of stress wave techniques[J]. Journal of Bridge Engineering, ASCE, 2012, 17(6): 847-856.
6	张清华, 卜一之, 李乔. 正交异性钢桥面板疲劳问题的研究进展[J]. 中国公路学报, 2017, 30(3): 14-30, 39.
	Zhang Qing-hua, Bu Yi-zhi, Li Qiao. Review on fatigue problems of orthotropic steel bridge deck[J]. China Journal of Highway and Transport, 2017, 30(3): 14-30, 39.
7	Deng P, Matsumoto T. Determination of dominant degradation mechanisms of RC bridge deck slabs under cyclic moving loads[J]. International Journal of Fatigue, 2018, 112: 328-340.
8	Liu Y K, Deng L, Zhong W J, et al. A new fatigue reliability analysis method for steel bridges based on peridynamic theory[J]. Engineering Fracture Mechanics, 2020, 236: 107214.
9	Su Q T, Dai C Y, Jiang X. Bending performance of composite bridge deck with T-shaped ribs[J]. Frontiers of Structural and Civil Engineering, 2019, 13(4): 990-997.
10	何亮, 饶志鹏, 凌天清, 等. 大跨径钢桥沥青铺装层裂缝行为研究进展[J]. 公路, 2018, 63(7): 71-81.
	He Liang, Rao Zhi-peng, Ling Tian-qing, et al. Progress of researches on fracture behavior of long-span steel bridge deck asphalt pavement[J]. Highway, 2018, 63(7): 71-81.
11	王朝辉, 郭瑾, 陈宝, 等. 桥面铺装结构的应用现状与发展[J]. 筑路机械与施工机械化, 2017, 34(12): 42-52.
	Wang Chao-hui, Guo Jin, Chen Bao, et al. Application status and development of deck pavement structures[J]. Road Machinery & Construction Mechanization, 2017, 34(12): 42-52.
12	程庆国, 徐蕴贤, 卢祖文. 钢纤维混凝土本构理论的研究、工程应用及发展[J]. 中国铁道科学, 1999(2): 3-11.
	Cheng Qing-guo, Xu Yun-xian, Lu Zu-wen. Research, engineering application and development of steel fiber concrete constitutive theory[J]. China Railway Science, 1999(2): 3-11.
13	Smarzewski P. Analysis of failure mechanics in hybrid fibre-reinforced high-performance concrete deep beams with and without openings[J]. Materials, 2018, 12(1): 101-124.
14	梁宁慧, 缪庆旭, 刘新荣, 等. 聚丙烯纤维增强混凝土断裂韧度及软化本构曲线确定[J]. 吉林大学学报: 工学版, 2019, 49(4): 1144-1152.
	Liang Ning-hui, Liao Qing-xu, Liu Xin-rong, et al. Determination of fracture toughness and softening traction-separation law of polypropylene fiber reinforced concrete[J]. Journal of Jilin University (Engineering and Technology Edition), 2019, 49(4): 1144-1152.
15	张春雷, 邵长宇, 苏庆田, 等. 球扁钢肋钢纤维混凝土组合桥面板正弯矩受力性能试验[J/OL]. [2023-08-19]. DOI: 10.13229/j.cnki.jdxbgxb.20220904 doi: 10.13229/j.cnki.jdxbgxb.20220904
	Zhang Chun-lei, Shao Chang-yu, Su Qing-tian. Experimental on positive bending behavior of composite bridge decks with steel-fiber-reinforced concrete and longitudinal bulb-flat ribs[J/OL]. [2023-08-19]. DOI: 10.13229/j.cnki.jdxbgxb.20220904 doi: 10.13229/j.cnki.jdxbgxb.20220904
16	Gribniak V, Arnautov A K, Norkus A, et al. Experimental investigation of the capacity of steel fibers to ensure the structural integrity of reinforced concrete specimens coated with CFRP sheets[J]. Mechanics of Composite Materials, 2016, 52(3): 401-410.
17	. 公路钢混组合桥梁设计与施工规范 [S].
18	戴昌源, 苏庆田, 冯小毛, 等. 纤维混凝土组合桥面板裂缝宽度计算方法[J]. 同济大学学报: 自然科学版, 2020, 48(6): 788-795.
	Dai Chang-yuan, Su Qing-tian, Feng Xiao-mao, et al. Crack width calculation method of fiber reinforced concrete composite bridge deck[J]. Journal of Tongji University (Natural Science), 2020, 48(6): 788-795.
19	. 钢-混凝土组合桥梁设计规范 [S].
20	高丹盈, 赵亮平, 冯虎, 等. 钢纤维混凝土弯曲韧性及其评价方法[J]. 建筑材料学报, 2014, 17(5): 783-789.
	Gao Dan-ying, Zhao Liang-ping, Feng Hu, et al. Flexural toughness and its evaluation method of steel fiber reinforced concrete[J]. Journal of Building Materials, 2014, 17(5): 783-789.
21	Amin A, Foster S J, Muttoni A. Derivation of the σ-w relationship for SFRC from prism bending tests[J]. Structural Concrete, 2015,16(1): 93-105.
22	Bencardino F, Rizzuti L, Spadea G, et al. Implications of test methodology on post-cracking and fracture behaviour of steel fibre reinforced concrete[J]. Composites Part B: Engineering, 2013, 46: 31-38.
23	Tiberti G, Minelli F, Plizzari G A, et al. Influence of concrete strength on crack development in SFRC members[J]. Cement and Comcrete Composites, 2014, 45: 176-185.
24	陈升平, Hwee Tan Kiang. 反分析法确定钢纤维水泥砂浆拉应力与裂缝张开位移关系[J].工程力学, 2008(4): 165-170.
	Chen Sheng-ping, Hwee Tan Kiang. Determining the stress-crack opening relationship of sfrm by inverse analysis[J]. Engineering Mechanics, 2008(4): 165-170.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

力学性能	数值
E_f/GPa	210
V_f/%	2
L_f/mm	13
d_f/mm	0.2
F_ftk/MPa	2850

试件编号	混凝土板开裂荷载/kN	中支点U肋下缘屈服荷载/kN	跨中U肋下缘屈服荷载/kN	中支点U肋屈曲荷载/kN	极限荷载（P_u）/kN
SFCB	350	1383	1453	1950	2019
SCCB	100	1204	1303	1750	1814

试件	荷载/kN	测试结果/mm	JTG/T D64-01-2015/mm	试件	荷载/kN	测试结果/mm	文献［18］/mm
SCCB	350	0.08	0.063	SFCB	350	0.04	0.045
	400	0.10	0.072		400	0.05	0.051
	450	0.12	0.081		500	0.06	0.063
	500	0.14	0.089		600	0.07	0.076
	600	0.14	0.110		700	0.09	0.090
	700	0.16	0.130		800	0.09	0.103
	800	0.16	0.140		900	0.10	0.115
	900	0.17	0.160		1000	0.10	0.137
	1000	0.17	0.170		1100	0.12	0.140
	1100	0.18	0.190		1200	0.12	0.153
	1200	0.20	0.200		1300	0.14	0.165
	1300	0.20	0.220		1400	0.14	0.178
	1400	0.22	0.240		1500	0.16	0.191
	1500	0.22	0.260		1600	0.20	0.203
	1600	0.24	0.260		1700	0.20	0.216

文献	ρ	f_t/MPa	f_t，re/MPa
［21］	0.005	3.85	1.15
	0.010	3.92	2.44
	0.005	4.03	0.60
	0.010	4.30	1.39
	0.005	6.35	4.95
	0.010	7.20	6.70
［20］	0.020	11.14	10.91
	0.015	9.10	8.94
	0.005	6.44	3.86
	0.010	6.85	5.89
	0.015	7.72	3.98
	0.020	9.30	8.60
［22］	0.010	14.00	13.80
	0.010	13.60	11.80
	0.010	9.90	8.00
	0.020	15.80	14.10
	0.020	15.30	13.70
	0.020	14.80	13.50
［23］	0.005	5.46	5.00
	0.010	4.91	3.75
	0.010	4.81	4.12
	0.010	5.97	4.35
	0.005	6.11	5.54
	0.010	4.94	7.51
	0.015	4.98	5.50
	0.015	4.63	3.75
	0.015	5.23	4.79
	0.005	4.60	4.12
	0.010	4.64	3.86
［24］	0.005	2.93	0.80
	0.010	4.07	1.70
	0.015	3.93	3.50
	0.020	3.96	3.70

[1]	安然,王有志. 剪力钉连接件拉剪共同作用抗剪性能[J]. 吉林大学学报(工学版), 2023, 53(9): 2554-2562.
[2]	左新黛,张劲泉,赵尚传. 在役混凝土T梁疲劳刚度退化及寿命预测方法[J]. 吉林大学学报(工学版), 2023, 53(9): 2563-2572.
[3]	顾正伟,张攀,吕东冶,吴春利,杨忠,谭国金,黄晓明. 基于数值仿真的简支梁桥震致残余位移分析[J]. 吉林大学学报(工学版), 2023, 53(6): 1711-1718.
[4]	吴春利,黄诗茗,李魁,顾正伟,黄晓明,张炳涛,杨润超. 基于数值仿真和统计分析的洪水作用下桥墩作用效应分析[J]. 吉林大学学报(工学版), 2023, 53(6): 1612-1620.
[5]	谭国金,孔庆雯,何昕,张攀,杨润超,朝阳军,杨忠. 基于动力特性和改进粒子群优化算法的桥梁冲刷深度识别[J]. 吉林大学学报(工学版), 2023, 53(6): 1592-1600.
[6]	江辉,李新,白晓宇. 桥梁抗震结构体系发展述评：从延性到韧性[J]. 吉林大学学报(工学版), 2023, 53(6): 1550-1565.
[7]	王峰,刘双瑞,王佳盈,宋佳玲,王俊,张久鹏,黄晓明. 尺寸和形状效应对多孔结构风阻系数的影响[J]. 吉林大学学报(工学版), 2023, 53(6): 1677-1685.
[8]	王俊,李加武,王峰,张久鹏,黄晓明. 简化U形峡谷风速分布及其对悬索桥抖振响应的影响[J]. 吉林大学学报(工学版), 2023, 53(6): 1658-1668.
[9]	王华,王龙林,张子墨,何昕. 基于裂缝宽度变化的连续刚构桥安全性预警技术[J]. 吉林大学学报(工学版), 2023, 53(6): 1650-1657.
[10]	冯宇,郝键铭,王峰,张久鹏,黄晓明. 非平稳极端风作用下大跨桥梁瞬态风致效应分析[J]. 吉林大学学报(工学版), 2023, 53(6): 1638-1649.
[11]	袁野. 温度和车辆作用下梁式桥梁结构固有频率分析方法[J]. 吉林大学学报(工学版), 2023, 53(6): 1702-1710.
[12]	刘子玉,陈士通,支墨墨,黄晓明,陈哲心. 可“临-永”转换抢修钢墩应急使用极限承载力[J]. 吉林大学学报(工学版), 2023, 53(6): 1601-1611.
[13]	张玥,刘传森,宋飞. 桥台背墙对连续梁桥地震易损性的影响[J]. 吉林大学学报(工学版), 2023, 53(5): 1372-1380.
[14]	兰树伟,周东华,陈旭,莫南明. 双柱式高墩桥梁整体稳定性的实用算法[J]. 吉林大学学报(工学版), 2023, 53(4): 1105-1111.
[15]	孙琪凯,张楠,刘潇,周子骥. 基于Timoshenko梁理论的钢-混组合梁动力折减系数[J]. 吉林大学学报(工学版), 2023, 53(2): 488-495.